标签:概率 ram 可能性 曲线图 nowrap idt 直接 这一 输入
六、逻辑回归
6.1 分类问题
对于二分类问题, 我们一般将结果分为0/1,在理解逻辑回归时可以引入感知机,感知机算是很早的分类器,但因为感知机是分布函数,也就是输出的值小于某一临界值,则分为-1,大于某一临界值,则分为1,但由于其在临界点处不连续,因此在数学上不好处理,而且感知机分类比较粗糙,无法处理线性不可分的情况,因此引入了逻辑回归,逻辑回归相当于用一个逻辑函数来处理回归的值,导致最终输出的值在[0, 1]范围内,输入范围是?∞→+∞,而值域光滑地分布于0和1之间。
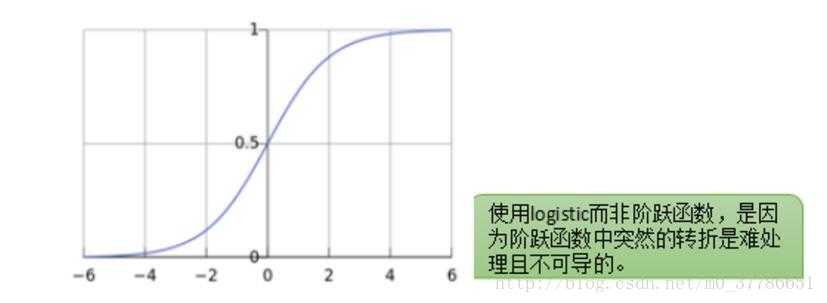
小于0.5的分为0类,大于0.5的分为1类。
6.2 hypothesis
逻辑回归的hypothesis可以表示为hθ(x)=g(θTX)hθ(x)=g(θTX), 其中g 代表逻辑函数(logistic function)是一个常用的逻辑函数为S形函数(Sigmoid function),公式为: g(z)=11+e?zg(z)=11+e?z。
在这里我们可以将hθ(x)的作用理解成,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity)即hθ(x)=P(y=1|x;θ)(条件概率事件, 在特定的x,θ下y=1的事件发生的概率), 根据判断概率是大于0.5,还是小于0.5来决定回顾ide值是1还是0.
6.3 判定边界
在做分类的问题的时候必然会有一条边界来对数据集进行分类,在这里我们可以看到对于逻辑回归只要z大于0,则输出1,小于0则输出0,即以θTx是大于0还是小于0来作为判定边界
6.4 代价函数(损失函数)
一般来说判定一个hypothesis的好坏都是看其代价函数是否足够小(当然在后面我们会看到代价函数并不是最小就一定合适,因为这样很可能会造成过拟合),
在这里m表示数据集中数据的个数,n表示数据集的维度
现在我们来看看怎么建立逻辑回归的代价函数,因为逻辑回归的y输出的值只有0和1, 因此用欧氏距离来表示其代价函数的话所获得的函数为非凸函数,无法通过梯度下降法获得其最小值,
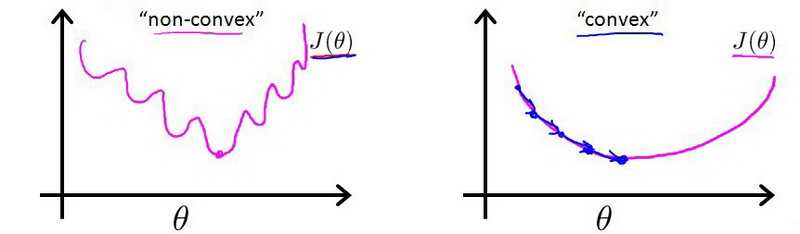
如上左图所示,欧氏距离表示的逻辑回归的代价函数曲线图,从曲线上看存在很多局部凸优化的点(即导数为0的点),无法下降到最低点,因此我们要根据逻辑回归的特点建立起代价函数
线性回归的代价函数为:J(θ)=1/m∑i=1m12(hθ(x(i))?y(i))2。
我们重新定义逻辑回归的代价函数为:J(θ)=1/m∑i=1mCost(hθ(x(i)),y(i)),其中

用cost(hθ(x), y)来表示hθ(x) 和y之间的误差, cost函数和hθ(x)的关系如下图所示,当y=1时,hθ(x)=1,cost函数等于0,hθ(x)=0, cost函数接近于正无穷,
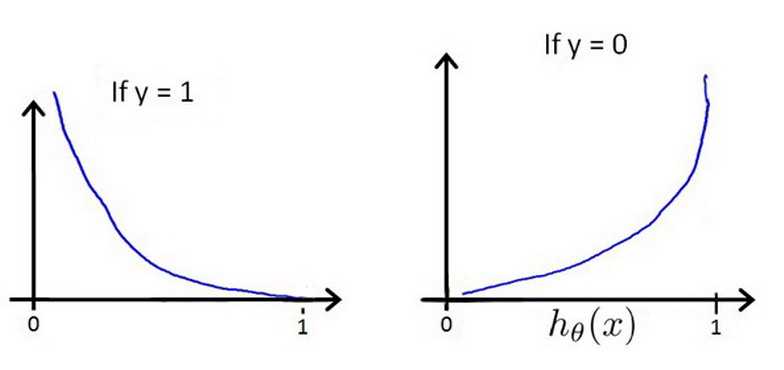
我们将上面的分步函数cost整合一下表示为Cost(hθ(x),y)=?y×log(hθ(x))?(1?y)×log(1?hθ(x)),将cost函数代入到代价函数中可以得到,J(θ)=1/m∑i=1m[?y(i)log(hθ(x(i)))?(1?y(i))log(1?hθ(x(i)))]
得到上述的代价函数后我们就可以得到其运用梯度下降来求其最小值,求导的时候可以将log看作ln,并不会影响最终的结果,这样可以得到梯度下降的模型
Repeat {
θj:=θj?α1/m∑i=1m(hθ(x(i))?y(i))x(i)j
(simultaneously update all )
}
在这里的导数看上去和线性回归一样,但是里面的hθ(x)是不一样的,逻辑回归这里是sigmod函数。
6.5 简化成本和梯度下降
在进行θ的梯度下降时,我们可以用for循环来执行每一次对θ向量中的各个元素的梯度下降,但更多的是直接向量化,对向量进行操作,另外在逻辑回归的梯度下降时也可以使用特征缩放(归一化)处理,使得代价函数更快的收敛。
6.6 高级优化
除了梯度下降法,还有一些更高级的优化算法, 比如fminunc, 共轭梯度法BFGS和L-BFGS,这些算法的优点是不需要自己去选择学习速率α, 因为算法内部回去寻找最合适的学习速率,而且这些算法的收敛速度也更快,但是它的缺点就是算法太复杂,学习该算法需要一定的时间。
6.7 多类别分类:一对多
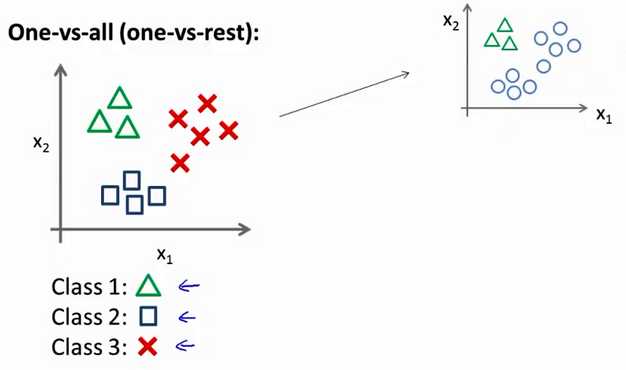
现实中存在很多多分类的问题,在处理多分类问题时可以借助二分类,首先我们看下多分类
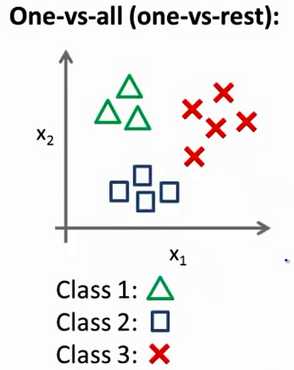
在处理上述问题的时候我们可以借助二分类来训练多个分类器处理多分类问题,原理很简单,如下图所示,当你在训练三角形的分类器时,可以将不属于三角形的归为负类(y=0,在这里我们采用逻辑回归来做二分类的问题),而属于三角形的归为正类(y=1),
然后对于圆形和正方形依次同样处理,对于多分类问题,所需要的分类器的个数和类别的个数一样,我们可以将该分类器集合表示为hθ(x),那最终我们怎么判别测试点该分为那个类别呢?我们可以将该测试点依次用上述的分类器集合中的分类器来进行判别,然后输入概率最大(即在进行多个分类器分类时被输出的次数最多的那一类)的那个类别。因此会处理二分类问题,就可以处理多分类的问题了。
七、正则化
正则化的引入主要是为了处理过拟合的问题,通过降低模型的复杂度来实现的,也可以看作是降低模型的维度,或者说减小θ向量的长度。
7.1 、过拟合的问题
过拟合的问题又可以称为泛化能力差,即你训练出来的模型只是针对你的训练集表现的很好,而对于一些未知的数据却不会输出正确的结果,这种现象的出现是因为你在训练的过程中把训练集中各元素的特有性质带进去了,那么这样的模型是不具备学习的(即机器学习是不可行的)。

上左图属于欠拟合现象,欠拟合好处理,通过减小代价函数,增大模型的复杂度就可以解决,上右图属于过拟合现象,这种现象往往是很难处理的,因为不易发现。
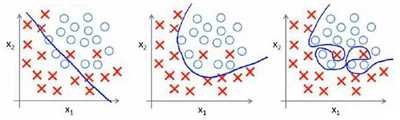
就以多项式来说,x的次数越高,拟合的会越好,很容易出现右边的情况,导致学习能力差。
解决过拟合的问题:一可以在数据处理时去除那些对结果输出影响不大的特征,二就是采用正则化,正则化是保留所有的特征,但是会减小参数的大小,即降低一些特征的权重。
7.2 代价函数的正则化
因为正则化的目的是减小参数的大小,而我们在求参数的时候又是通过求代价函数的最小值来获得的,因此通过对代价函数加入正则化参数来实现这一目标。
hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4,我们来看这个模型,过拟合往往是由于多项式中的高阶项造成的,在这里我们只要使这些高阶项的参数很小就可以很好的避免过拟合的现象,在这里我们假设x3,x4位高阶项,则我们可以修改代价函数
修改后的代价函数如下:minθ 1/2m[∑i=1m(hθ(x(i))?y(i))2+1000θ3+10000θ4],通过在θ前面加入一个大的系数,当要是的代价函数趋于0时,只有θ3,θ4趋于0才能实现。这种操作称为对特征的惩罚,但现实中我们不知道要惩罚哪些特征,因此我们会选择对所有的特征进行
惩罚,至于惩罚的力度我们让代价函数最优化的软件来决定,因此代价函数可以表示为
J(θ)=12m[∑i=1m(hθ(x(i))?y(i))2+λ∑j