标签:rip polar line int() 保留 sam span 论文 ros
逆时针给出n个凸多边形的顶点坐标,求它们交的面积。例如n=2时,两个凸多边形如下图:
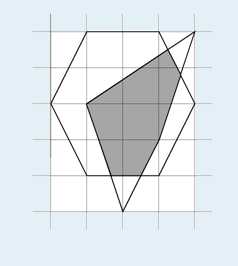
则相交部分的面积为5.233。
第一行有一个整数n,表示凸多边形的个数,以下依次描述各个多边形。第i个多边形的第一行包含一个整数mi,表示多边形的边数,以下mi行每行两个整数,逆时针给出各个顶点的坐标。
输出文件仅包含一个实数,表示相交部分的面积,保留三位小数。
2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0
5.233
100%的数据满足:2<=n<=10,3<=mi<=50,每维坐标为[-1000,1000]内的整数
我会半平面交啦啦啦~~~
半平面交我不用多说,有篇论文写的太好啦! Orz
https://wenku.baidu.com/view/c750720bf78a6529647d53ae.html
(顺面可以学一波外语~嘿嘿嘿~)
我就精心画几张图来表示一下啦~~~
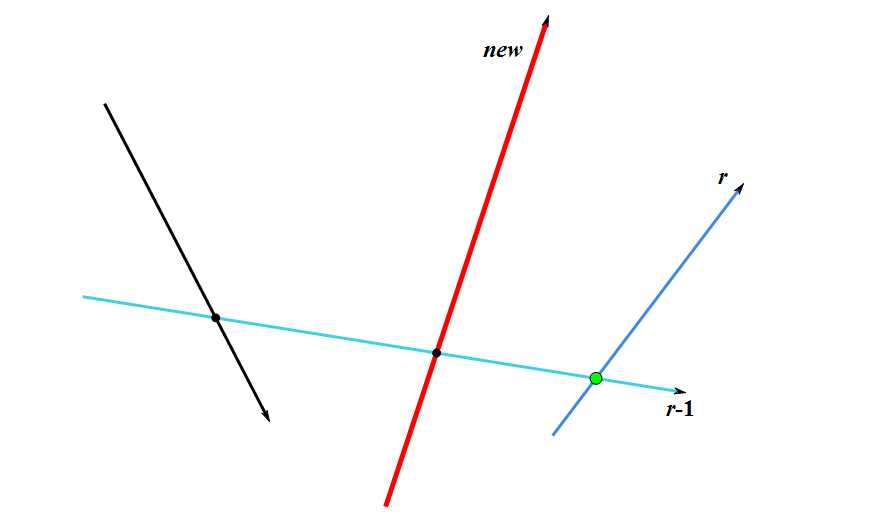
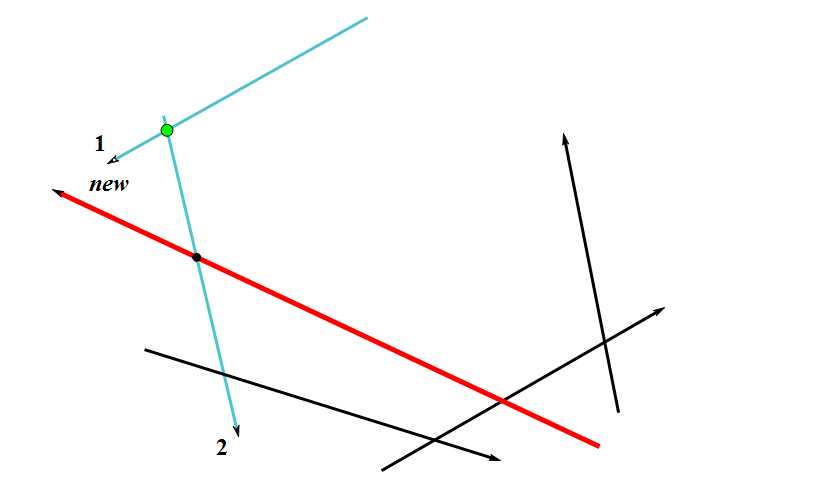
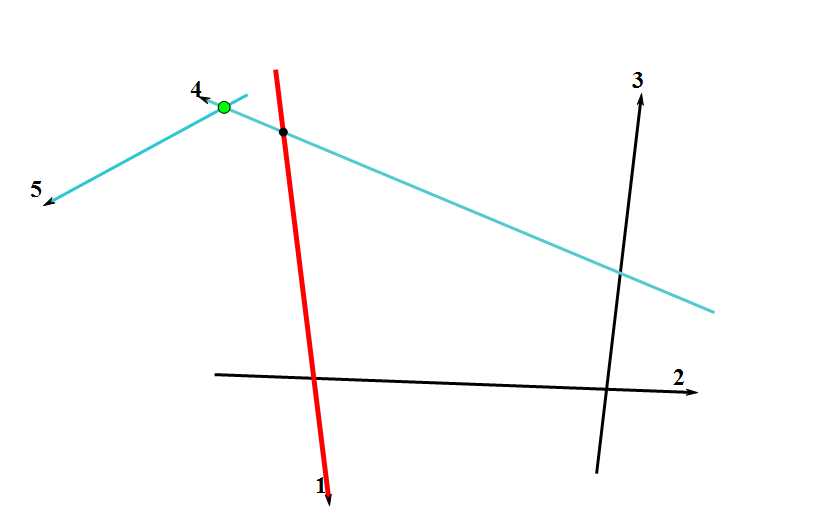
#include<bits/stdc++.h>
using namespace std;
struct vec{
double x, y;
vec() {}
vec(double a, double b) { x = a, y = b; }
vec operator - (const vec &A){ return vec(x - A.x, y - A.y); }
};
struct Line{
vec A, B; double polar;
bool operator < (const Line &A)const{ return polar < A.polar; }
}linL, lpl[505], lpd[505];
const int eps = 1e-8;
vector<Line> L;
vector<vec> ans;
int n, m, l, r;
double cross(vec A, vec B){ return A.x * B.y - A.y * B.x; }
bool onleft(vec A, Line X){ return cross(X.B - X.A, A - X.A) > 0; }
vec inter(Line A, Line B){
double s1, s2, k; vec ret;
s1 = cross((A.B - A.A), (B.B - A.A));
s2 = cross((B.A - A.A), (A.B - A.A));
k = s2 / (s1 + s2);
ret.x = B.A.x + k * (B.B.x - B.A.x); ret.y = B.A.y + k * (B.B.y - B.A.y);
return ret;
}
inline void putit()
{
int mx; vec p[55]; scanf("%d", &n);
for(int i = 1; i <= n; ++i){
scanf("%d", &mx);
for(int j = 1; j <= mx; ++j) scanf("%lf%lf", &p[j].x, &p[j].y);
for(int j = 1; j < mx; ++j){
linL.A = p[j], linL.B = p[j + 1];
linL.polar = atan2(linL.B.x - linL.A.x, linL.B.y - linL.A.y);
L.push_back(linL);
}
linL.A = p[mx], linL.B = p[1];
linL.polar = atan2(linL.B.x - linL.A.x, linL.B.y - linL.A.y);
L.push_back(linL);
}
}
inline void HPI()
{
sort(L.begin(), L.end());
int len = L.size() - 1;
int siz = 1; lpd[1] = L[0];
for(int i = 1; i <= len; ++i){
if(L[i].polar != lpd[siz].polar) { lpd[++siz] = L[i]; continue; }
if(onleft(L[i].A, lpd[siz])) lpd[siz] = L[i];
}
l = 1; r = 2; lpl[1] = lpd[1], lpl[2] = lpd[2];
for(int i = 3; i <= siz; ++i){
while(l < r && !onleft(inter(lpl[r], lpl[r - 1]), lpd[i])) r--;
while(l < r && !onleft(inter(lpl[l], lpl[l + 1]), lpd[i])) l++;
lpl[++r] = lpd[i];
}
while(l < r && !onleft(inter(lpl[r], lpl[r - 1]), lpl[l])) r--;
while(l < r && !onleft(inter(lpl[l], lpl[l + 1]), lpl[r])) l++;
}
inline void print()
{
lpl[r + 1] = lpl[l];
for(int i = l; i <= r; ++i) ans.push_back(inter(lpl[i], lpl[i + 1]));
if(ans.size() < 3) {printf("0.000"); return;}
double ret = 0;
ans.push_back(ans[0]);
int len = ans.size() - 1;
for(int i = 0; i < len; ++i)
ret += cross(ans[i], ans[i + 1]);
printf("%.3lf", fabs(ret) / 2);
}
int main()
{
putit();
HPI();
print();
return 0;
}标签:rip polar line int() 保留 sam span 论文 ros
原文地址:https://www.cnblogs.com/LLppdd/p/8837176.html