Palindrome Number

标签：ever   分享图片   info   题目   思想   rom   但我   通过   pre   

第三道简单题。啊好懒啊已经不想做了 = =。这样暑假在家肯定会废。emm简单题一共200道的样子。我的目标是接下来的三个礼拜，每个礼拜做10道!!!希望回国前能做到50道。加油！

这道题考的是回文结构，之前我在网易的笔试里也碰到了回文结构的相关题目，回文结构大概比较容易被考察。

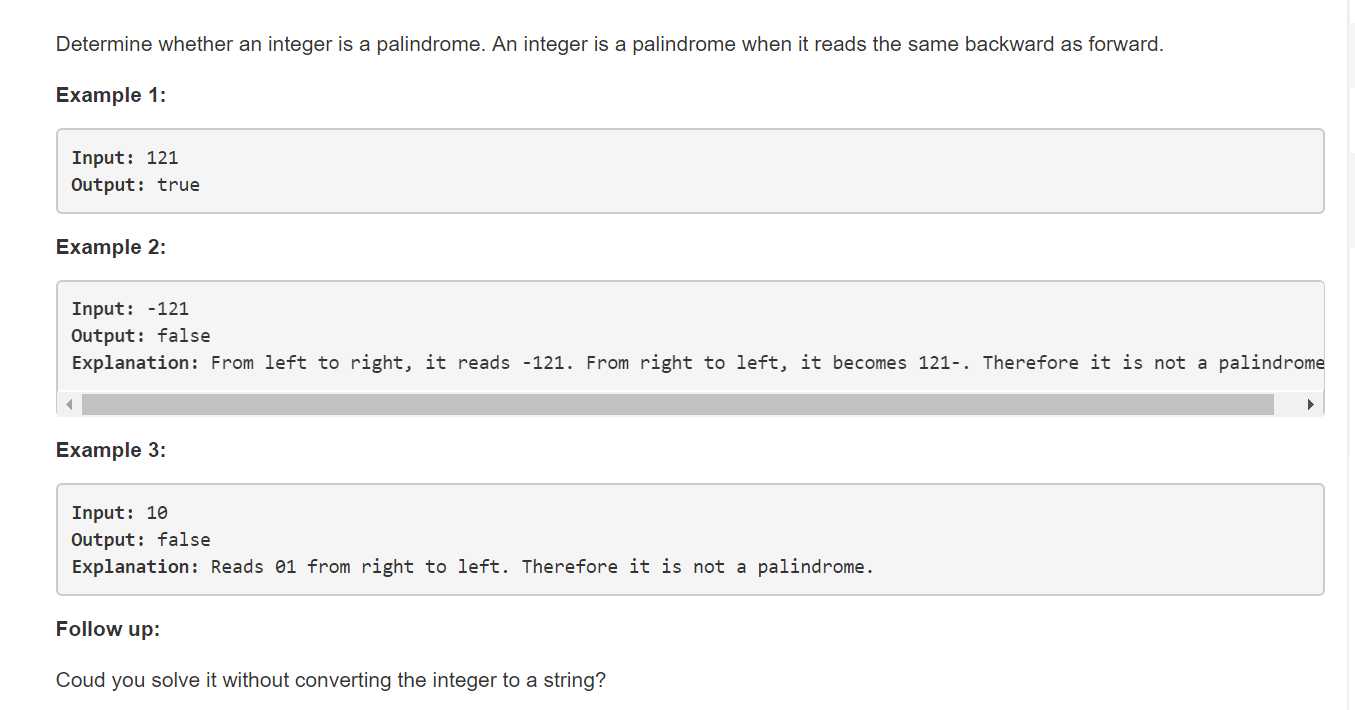
Example 2说明了所有负数都不可能是回文结构。

Example 3说明结尾带0的也一定不是回文结构啦。结尾带0，反转后0一定在开头，而一般的数0都没法出现在开头的。

这两种特殊情况可以先拎出来处理。

剩下的我就套用了一下上一题的思路啦嘻嘻嘻。

不过在处理过程中我错了一个地方！输入为0的时候，0应该也是回文结构，但我通过x%10==0这个if条件直接判定为false返回了。所以我就贼兮兮地又加了个判定条件。这是我地最后代码。

class Solution {
public:
    bool isPalindrome(int x) {
        int oridinary=x; //save x first
        if(x<0||(x%10==0&&x!=0)) return false;
        int res=0;
        while(x){
            res = res*10+x%10;
            x = x/10;
        }
        return res==oridinary;
            
    }
};

emm只打败了37.49%的人。

另外一种解答：

class Solution {
public:
    bool isPalindrome(int x) {
        if(x<0|| (x!=0 &&x%10==0)) return false;
        int sum=0;
        while(x>sum)
        {
            sum = sum*10+x%10;
            x = x/10;
        }
        return (x==sum)||(x==sum/10);
    }
};

这种方法的思想是只reverse一半，然后拿前一半与另一半比较。奇数的情况是后一半的位数比前一半多一位，所以在最后return的时候我们会考虑x==sum/10的情况。偶数的情况呢是前一半和后一半的位数正好相等。

我觉得这种方法应该比我的方法效率高才对……但是只打败了30%的人。

Palindrome Number

标签：ever   分享图片   info   题目   思想   rom   但我   通过   pre   

原文地址：https://www.cnblogs.com/haofeng5/p/8846718.html