标签：第一步 深度 总结 使用 缓存 元素 eigen 统一 球面
VINS-mono详细解读
极品巧克力
Vins-mono是香港科技大学开源的一个VIO算法，https://github.com/HKUST-Aerial-Robotics/VINS-Mono，是用紧耦合方法实现的，通过单目+IMU恢复出尺度，效果非常棒。
感谢他们开源，我从中学到了非常多的知识。源码总共有15000多行，我在通读完程序之后，结合参考文献，把程序背后的算法理论都推导了一遍，总结成了本文，与各位分享。
本文目标读者：对vins-mono有一定了解的SLAM算法工程师。由于程序里有非常多的实现细节，建议读者在读本文前，先读一遍vins-mono的程序。
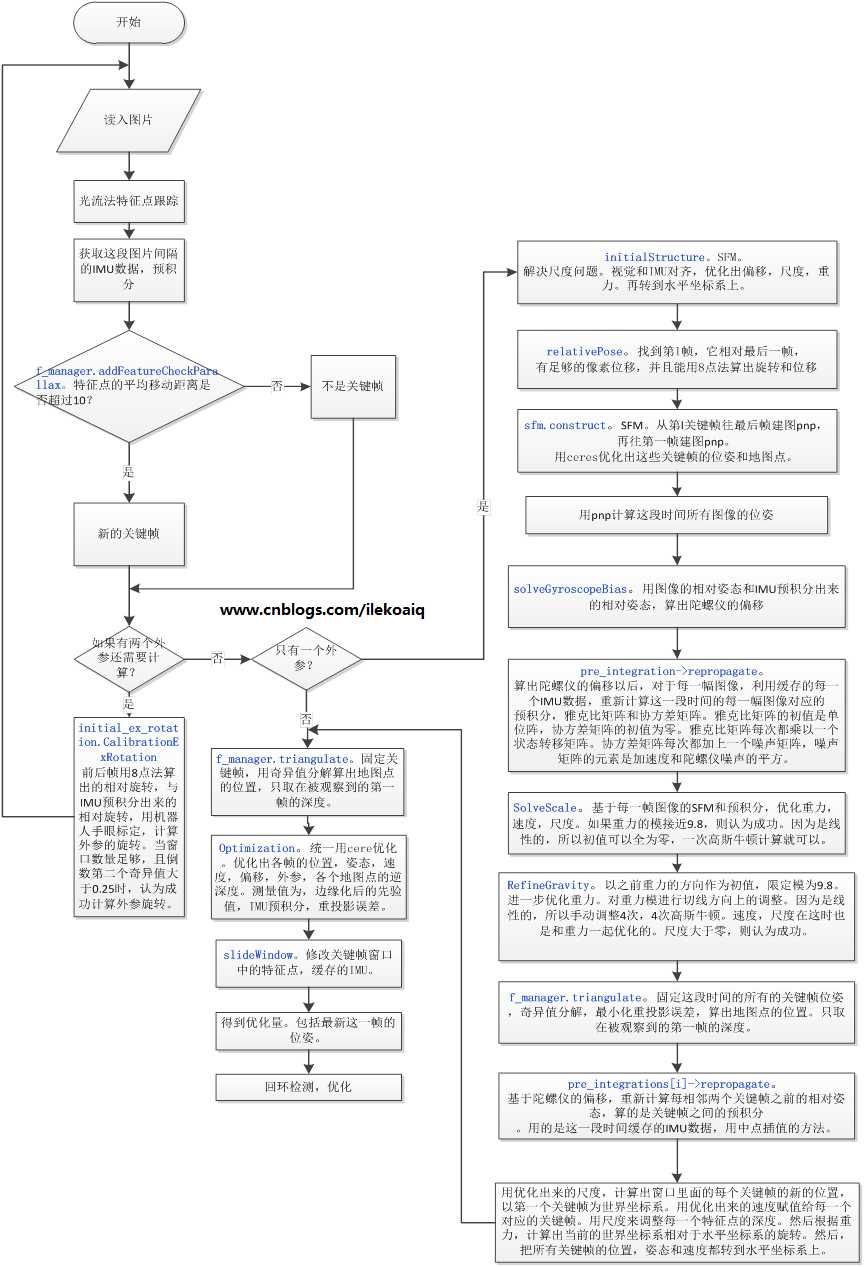
首先用cv::goodFeaturesToTrack在第一帧图像上面找最强的150个特征点，非极大值抑制半径为30。新的特征点都有自己的新的对应的id。然后在下一帧过来时，对这些特征点用光流法进行跟踪，在下一帧上找匹配点。然后对前后帧中这些匹配点进行校正。先对特征点进行畸变校正，再投影到以原点为球心，半径为1的球面上，再延伸到深度归一化平面上，获得最终校正后的位置。对于每对匹配点，基于校正后的位置，用F矩阵加ransac来筛选。然后再在匹配上的特征点之外的区域，用cv::goodFeaturesToTrack搜索最强的新的特征点，把特征点数量补上150个。
最后，把剩下的这些特征点，把图像点投影回深度归一化平面上，再畸变校正，再投影到球面上，再延伸到深度归一化平面上，得到校正后的位置。把校正后的位置发送出去。
特征点跟踪和匹配，就是前一帧到这一帧的，一帧帧继承下去。或者生成新的特征点。
用机器人手眼标定的方法，计算出外参中的旋转。
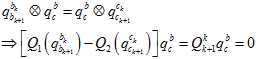
其中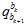
是陀螺仪预积分得到的，
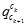是用8点法对前后帧对应的特征点进行计算得到的。详细见《Monocular Visual-Inertial State Estimation With Online Initialization and Camera-IMU Extrinsic Calibration》。
先在关键帧窗口里面，找到第l帧，第l帧与最后一帧有足够的像素位移，并且能用8点法算出旋转和位移。以l帧的姿态为世界坐标系。先从l帧开始与最后一帧进行三角定位，再用pnp估计出下一帧的位姿，下一帧再与最后一帧三角定位得出更多的三维点。重复到倒数第二帧。从l帧开始往第一帧，逐渐帧pnp，再与第l帧进行三角定位得到更多的三维点。每帧pnp时的位姿初值都用上一个关键帧的的位姿。剩下的那些还没有被三角定位的特征点，通过它被观察到的第一帧和最后一帧进行三角定位。
固定住l帧的位置和姿态，固定住最后一帧的位置。因为这时候的图像位姿和点的位置都不太准，所以用ceres统一一起优化图像位姿和三维点位置，优化重投影误差。优化的测量值是，特征点在每帧中被观察到的位置，可以转成重投影误差约束。有关的自变量是，每帧图像的位姿，特征点的三维坐标。
优化完成之后，即用ceres优化出这些关键帧的位姿和地图点后，再用pnp算出在这段时间区域内的所有图像的位姿。每个图像的计算都用下一个关键帧的位姿来当pnp的初值。
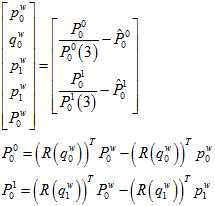
程序里面没有求雅克比，而是用自动求导的方法。
在2.1中已经根据连续图像的相对旋转算出相机和IMU间的外参旋转了，现在要再根据上一节2.2中的SFM算出来的各帧图像的相对旋转来计算出陀螺仪的偏移。
就是根据前后帧之间的根据陀螺仪预积分出来的旋转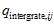
与基于SFM图像算出来的旋转转换到IMU坐标系的相对旋转
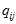之间的向量差的两倍。
在程序里面，每次算出的图像的姿态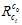
，都会转换成
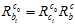。然后在计算相对IMU的姿态时，就用
。
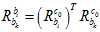这里是采用了近似计算的方法。其实就是把角度的残差转换成了角轴差的形式。详见《从角轴到四元数微分方程》和《on-manifold详细解读》。
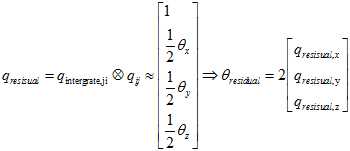
这个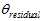
关于陀螺仪的偏移求导，得到雅克比矩阵。然后再根据高斯牛顿法算出陀螺仪偏移。
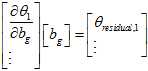
算出陀螺仪的偏移以后，对于每一幅图像，利用缓存的每一个IMU数据，重新计算这一段时间的每帧图像对应的预积分，雅克比矩阵和协方差矩阵。
雅克比矩阵的初值是单位阵，协方差矩阵的初值为零。雅克比矩阵每次都乘以一个状态转移矩阵。协方差矩阵每次都左右乘状态转移矩阵，再加上一个噪声矩阵，噪声矩阵就是加速度和陀螺仪噪声所形成的噪声协方差矩阵。
从2.3之后，认为陀螺仪是准确的，每帧图像的姿态也都是准确的。
速度，重力和尺度对齐，其实就是，每一帧对后一帧的位置，速度的预测值，与当前值的误差。当前值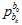
的位置，是SFM位置
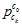通过外参
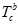计算过来，给的。与这有关的自变量是每帧的速度，重力，尺度。速度，重力，尺度，给的初值都是零。
以第一帧和第二帧为例。
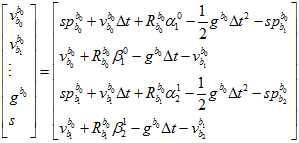
因为速度，重力尺度的初值全部都是零，所以第一步，这里残差的计算可以简化成如下。
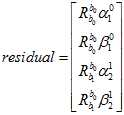
但雅克比的计算，还是得用原来的表达式算。
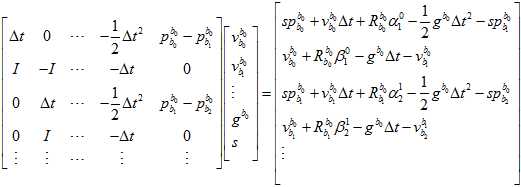
虽然给的初值是零，但因为雅克比矩阵里面的元素都是与自变量无关的常数，表示这是线性的，所以只用高斯牛顿法计算一次就可以了。只要数据足够，就能算出比较准确的值。
其中，当前值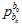
的位置，是SFM位置
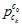通过外参
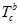计算过来，给的。机器人手眼标定。
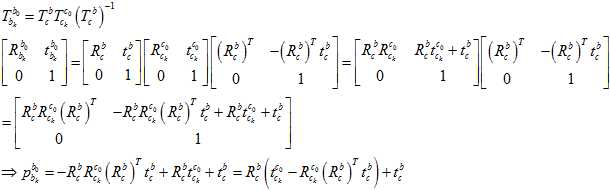
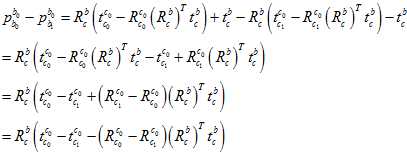
当然，程序里面实际上是把残差转换成了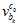
这样的奇怪的坐标系下，结果就会像《technical report》里面的公式18那样子，全部都乘以
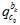。但是，我觉得像我上面那样的用机器人手眼标定的方法来表示，会比较方便容易易懂直观明了，更不容易在写表达式的时候出错。
虽然给的初值是零，虽然只用高斯牛顿法计算一次，但只要数据足够，也能算出比较准确的值。每增加一帧，就用高斯牛顿法全部计算一次，速度重力尺度的初值全部都是零。因为反正都可以用高斯牛顿法一次算出结果，所以就不用继承之前的值来优化。
直到优化后的重力接近9.8，比如重力模在[8.8,10.8]区间内。这个方法挺好的，不用先验知识就把重力优化到9.8，结果令人信服。
程序里面，会把关于尺度求导得到的雅克比除以100，这就意味着，尺度这个变量对残差的影响力减弱了100倍。最终为了能消去残差，优化后的尺度会比实际的大100倍。得到后，要再除以100。这么做的目的，应该是要让尺度的精度更高。
每次都直接把这一块的雅克比矩阵和对应的残差，转换成H矩阵的形式，直接加到H矩阵上。为什么要这样做呢？为什么不把全部的雅克比矩阵算好之后再一次性地转换成H矩阵。因为雅克比矩阵太巨大了，而且非常稀疏，里面很多元素都是零。所以，可以直接根据雅克比矩阵的计算表达式知道哪些位置是非零的，然后非零的位置对应相乘加到入H矩阵中对应的位置，即节省存储空间，又能加快计算。
在2.4计算出来一个相对准确的值的基础上，还要再加个约束，即重力的模为9.8。可以有两个方法。
第一个方法是，直接在2.4的残差约束里面增加一个，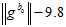
。
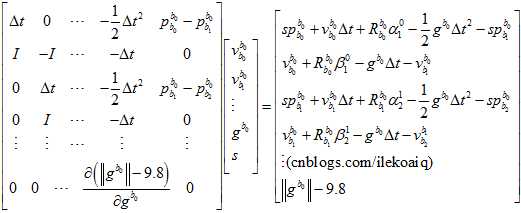
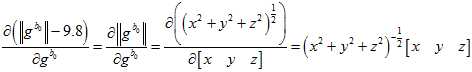
但是，如果这样的话，雅克比矩阵里面就有了与自变量有关的元素，就不是线性的了。这样子，计算起来就会比较麻烦，可能需要迭代很多次。
所以，采用方法二。
对模的方向进行优化。2.4的优化仅仅是提供一个较好的重力的方向。
直接给重力一个初值，模的大小就是9.8，方向的初值是2.4中优化后的重力的方向。对这个重力，在切线上调整它的方向。
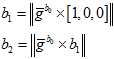
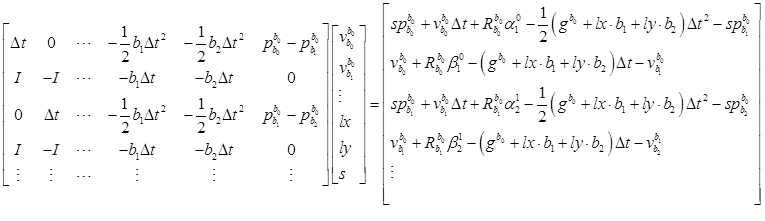
因为是线性的，所以自变量的初值直接全部设为零。直接一步高斯牛顿法，算出最优值。用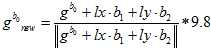
来更新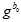
。
重复上述步骤四次，即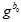
更新四次后，就认为这些变量，速度，重力，尺度都已经优化到一个很优的值了。这时候，尺度应该是大于零的。
手动在切线上调整，然后再控制模。其实，就是由自动的非线性优化，改成了手动的线性优化，用来控制迭代次数。
用奇异值分解的方法，对每一个特征点都优化重投影误差最小化，优化出它在被观察到的第一帧的相机坐标系下的位置，然后只把深度拿过来用。设它们在被观察到的第一帧的相机坐标系下的齐次坐标为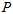
，其它观察帧相对观察第一帧的位姿为
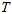。已知它在每帧的投影点，最小化它在每帧的重投影误差。相当于是寻找空间中的一点，与，每帧的光心从投影点发出的射线，距离最小。
与2.2SFM时算出的地图点的区别在于，2.2SFM时算出的地图点是ceres优化出来的关键帧及其对应的地图点。而这里，是固定这段时间的所有的关键帧，这些关键帧的姿态在2.3后期算出陀螺仪偏移后，已经调整过了。奇异值分解，最小化重投影误差，算出地图点的位置。只取在被观察到的第一帧的深度。因为在这时候，各个图像的位姿已经相对比较准确了，所以与2.2中的cere图像位姿和地图点全部优化不同，这里只需要优化地图点就可以了。
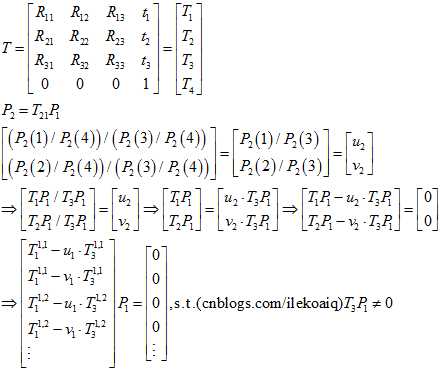
在算奇异值分解时，还要增加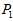
模为1的约束。齐次坐标
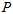为一个四维的向量，这样子，通过增加模为1的限制，就可以用奇异值分解来优化，这就是这里用齐次坐标的好处。（在程序实际运行的时候，上面方程的左边，还除以了归一化的模，但不会影响计算结果）
基于2.3中的陀螺仪的偏移，重新计算每相邻两个关键帧之前的相对姿态，算的是关键帧之间的预积分。用的是这一段时间缓存的。IMU数据，用中点插值的方法。
然后用2.5中优化出来的尺度，计算出窗口里面的每个关键帧的新的位置，它们相对于第一个关键帧的位姿，把第一个关键帧当作世界坐标系。用2.5中优化出来的速度赋值给每一个对应的关键帧。用尺度来调整每一个特征点的深度。
然后根据重力，计算出当前的世界坐标系相对于水平坐标系的旋转，即第一个关键帧相对于水平坐标系的旋转。然后，把所有关键帧的位置，姿态和速度都转到水平坐标系上。
每新进来一张图片，上面有跟踪出来的特征点。
对于f_manager中的feature列表中的那些还没有深度的特征点，用奇异值分解计算出一个它的坐标，使得它在它被观察到的每帧图像上的重投影误差最小。它的坐标用在它被观察到的第一帧图像的相机坐标系的深度表示。因为它还有它在被观察到的每帧图像上的归一化坐标。
然后用cere来优化。结合各个关键帧的位姿，各个相机的外参，边缘化的信息，与预积分的误差，每个特征点的重投影误差，回环闭环误差。进行优化。
然后滑动窗口。判断边缘化的条件是，是否进来一个新的关键帧。
如果有边缘化的话，则把窗口中最前面的一个关键帧滑掉。然后把第一次被这个关键帧观察到的特征点，都转移到新的第0个关键帧上。如果没有边缘化的话，则把之前最新的这一帧用进来的最新的这一帧替换掉。
窗口的大小默认是10。
每当进来一个新的图像帧的时候，首先判断它与窗口里面存储的之前的那一帧的的相对位移，就是与第10帧的特征点的相对位置，用特征点的相对位移来表示。
如果特征点的平均相对位移大于某一个阈值，就认为是一个新的关键帧。就把这个新的关键帧压入到窗口里面，就是压入到第10个位置，然后其它的关键帧都往前移动。第一个位置的关键帧被移出去，边缘化。
如果不是新的关键帧，就把之前的第10帧边缘化掉，这个新的一帧替换成为第10帧。
总之，无论是哪种情况，这个新的一帧肯定都会成为窗口里面的第10帧。
边缘化，是在优化之后才进行的，而且最新的这帧上面观察到的新的特征点并不参与优化。所以，优化的时候，是包括最新的这一帧的11帧的姿态，以及前10帧的特征点在每一帧的投影，包括它们在最新这帧的投影点。所以para_Pose之类的待优化变量的数组长度是11。
对于f_manager中的feature列表中的那些还没有深度的特征点，如果它被之前2帧以上的关键帧观察到过，用奇异值分解计算出一个它的坐标，使得它在它被观察到的每帧图像上的重投影误差最小。它的坐标用在它被观察到的第一帧图像的相机坐标系的深度表示。因为它还有它在被观察到的每帧图像上的归一化坐标。
如果以后要把VINS改用深度相机的话，可以在这里修改。1.信任深度相机，这个点被观察到的第一次的位置就是准确值，直接加入地图点。2.怕深度相机有误差，所以加判断，这个点在它被观察到的连续两帧里面，在世界坐标系中的三维坐标不能相差太大，如果相差太大，就把它的第一帧的观察记录删掉。如果相差不大，就取两个三维坐标的平均值，作为该点的三维位置，加入地图点。3.还可以借鉴ORBSLAM里面的筛选地图点的方法，该点需要在连续几帧中被观察到，并且这连续几帧，观察到的它在世界坐标系中的三维坐标，不能相差太大，就认为它是一个好的点，加入地图点。之后的cere优化中，就不再优化地图点，可以极大地加快优化速度。
要优化的目标是各帧的位置，姿态，速度，偏移，以及相机的外参，以及每一个特征点在它被观察到的第一帧的深度。即，要优化的自变量是。
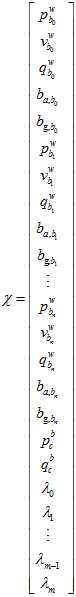
要拟合的目标是，之前边缘化后的先验值，前后帧之间的IMU的预积分值，再加上前后帧之间的偏移的差的约束，每一个特征点的重投影位置。
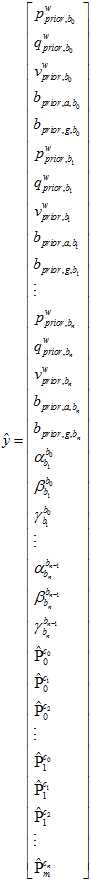
其中，prior代表先验值。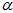
代表前后帧之间的加速度计的二次积分，
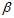代表前后帧之间的加速度计的一次积分。
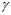代表前后帧的陀螺仪的一次积分。
另外，要再加上前后帧之间的偏移的差的约束。
所以，在当前的自变量的情况下，与目标的残差为residual，表示如下。
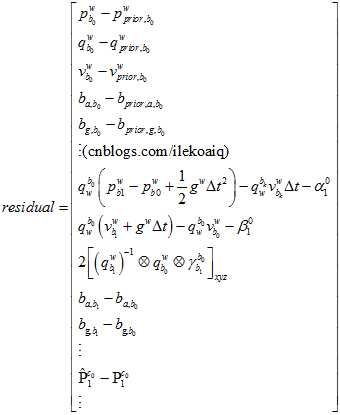
其中，与先验值的残差，为了计算方便，可以再转换到之前的舒尔补之后的残差空间里。用第一状态雅克比。因为在上一次边缘化之前，已经优化之后的残差，舒尔补之后的residual，已经是最小二乘结果，它反馈到自变量上面是接近于零（因为各个方向的量都抵消了）。所以，如果这时候，如果对自变量调整了dx，则与之前的舒尔补后的值的残差会增加J*dx。
其实，在这里，不仅仅是要表示与之前的先验值的差，而是要表示在之前的误差的基础上面叠加上来的误差。因为之前的误差是最小二乘结果，而不是全零。
//每个关键帧的位姿与先验值的不同，会造成残差项增大
Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;
所以，第一部分的雅克比就是之前边缘化后的雅克比，误差就是之前的误差再加上新的误差。
第一部分，要拟合的约束目标是，每帧与之前边缘化后的位姿、速度和偏移不能相差太大。残差用，之前的边缘化后的残差，加上，现在的自变量与之前边缘化后的自变量的相差的值乘以第一状态雅克比。与之相关的自变量是，每帧的位姿，速度和偏移，相机与IMU的相对位姿。残差关于要优化的自变量求导，得到雅克比矩阵。
为了简化表示，可以把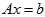
，里面的A和b矩阵按行分成一块一块的来表示。
从第二部分开始。要拟合的测量值目标是，IMU的加速度计和陀螺仪的预积分。可以转换成实际值与预测值的位姿差来约束。另外还要加上前后偏移接近的约束。与这有关的自变量是，前后帧的位姿，速度，偏移。
其实就是，前一帧基于IMU对后一帧的位置，姿态，速度，偏移，的预测值，与当前值的，误差。
每次迭代之后，重新算误差（需要人为写出算误差的程序）。都会用最新的偏移与之前的偏移的差，重新计算两帧之间的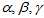
，因为先前预积分的时候已经算好了预积分的值关于偏移的导数。所以，这里直接根据偏移差乘以导数，就能一下调节预积分的值。明明已经有了预积分关于偏移的雅克比了，为什么这里要这样子把偏移单独拿出来算新的预积分，而不是偏移和预积分一起直接优化呢？每迭代一次都要调整一次，为什么不多优化几次，最后再累加呢？因为当新的偏移与旧的偏移相差较大的时候，就不再使用之前预积分关于偏移的雅克比了，需要repropagate，重新计算新的预积分值和雅克比。但程序里把，判断偏移相差较大后重新传播这一块注释了。预积分关于偏移的雅克比矩阵的计算为，状态向量转移或相加，则对应的雅克比矩阵也转移或相加，详见《on-manifold详细解读》。
非线性迭代，每次迭代后，根据残差和雅克比调整自变量的值，再根据调整后的自变量计算出新的残差，再计算出新的雅克比，如此循环。这样子，因为有残差里面的预积分关于偏移的导数，每次迭代后，调节自变量里面的偏移的值后，再计算新的残差时，就方便了。
然后，第三部分，要拟合的测量值目标是特征点在各帧图像上的测量位置。可以转换成重投影误差来约束。与这有关的自变量是，该特征点被观察到的第一帧和被观察到的另外一帧的位置和姿态，相机和IMU之间的相对位姿，特征点在第一帧的深度。
其实就是，对每一个地图点的预测的投影点与实际的投影点的误差。
全展开残差项可以表示为，
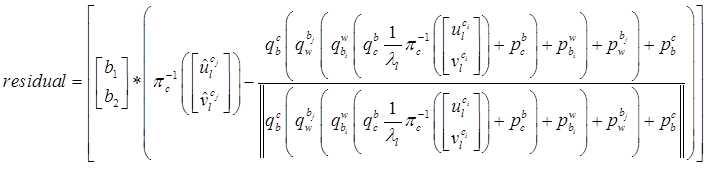
其中，
是当前的原点到测量单位球面点的向量
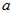，在球面上的切向单位向量。
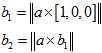
它与误差向量相乘，就相当于误差向量在这两个切向向量上的投影。因为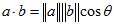
。
化简后，可以表示为，
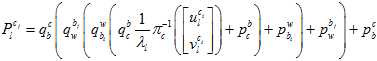
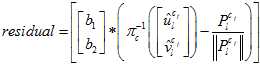
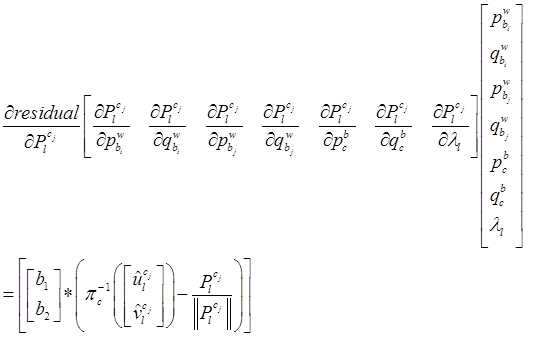
其中，链式求导，一步步传导下去。
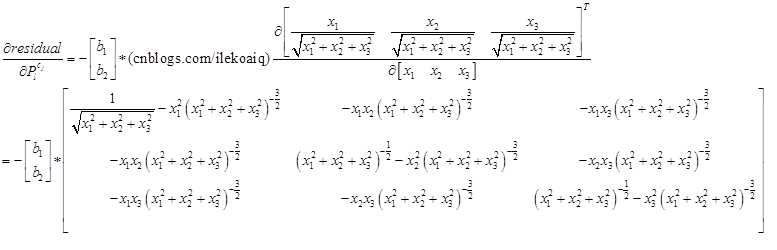
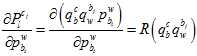
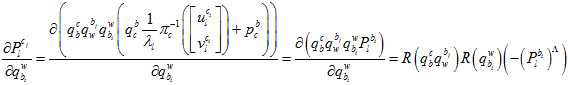
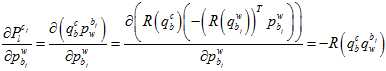
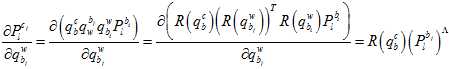
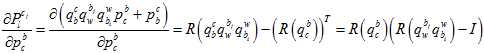
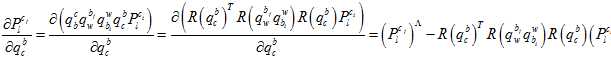
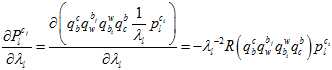
因为在上述的雅克比矩阵里面，都有自变量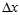
了，所以它是非线性的，只能通过优化的方法一步步迭代。
H*x=JT*residuals，H=JT*J。
基于舒尔补来边缘化。
用奇异值分解的技巧来得到新的雅克比矩阵，作为先验雅克比。由b反过去算残差，作为先验值，在下一次优化时使用。
其实，与《on-mainifold》里面的舒尔补的方法，本质上是一样的。
关于边缘化，还可以再参考http://blog.csdn.net/heyijia0327/article/details/52822104。
如果窗口里存在有回环帧的对应帧的话，则先找到对应帧与回环帧的匹配点id和位置，特征点匹配用的是在一定范围内匹配描述子。特征点匹配完之后，然后只保留这些匹配上的id和特征点位置，给front_pose，id用对应帧的id，特征点位置用回环帧的位置。其实，就是把对应帧的id赋给匹配上的回环帧的特征点。然后给front_pose.loop_pose对应帧的姿态作为初值，然后用窗口里面的点的重投影误差来优化front_pose.loop_pose，点的逆深度，点被观察到的第一帧的位姿。
窗口优化之后，比较对应帧与front_pose.loop_pose的yaw角是否相差太大，如果相对yaw角大于30度或相对位置大于20的话，就认为这是错误的回环，删除这个回环。因为这时候，这个对应帧还在窗口里面，还没有滑出去回环闭环。所以，这样也可以及时把DBow找出来的错误的回环，删掉。
其实，就是把回环帧放到窗口里面来优化，优化出回环帧的位姿，然后再算出回环帧和对应帧的相对位姿。然后把这个相对位姿，作为后面的回环4自由度优化的测量值。具体是，优化出回环帧在窗口里面的位置后，算出对应帧相对于回环帧的位姿。
新的关键帧在加入关键帧数据库的时候，作为对应帧，在关键帧数据库里面去找回环帧。如果用DBOW找到回环帧，使用cur_kf->findConnectionWithOldFrame(old_kf, measurements_old, measurements_old_norm, PnP_T_old, PnP_R_old, m_camera);。先用searchByDes 去找匹配点，然后用cv::findFundamentalMat(un_measurements, un_measurements_old, cv::FM_RANSAC, 5.0, 0.99, status);筛选匹配点，再用对应帧自带的地图点结合solvePnPRansac，得到回环帧的位姿PnP_T_old。PnP_T_old作为回环帧位姿loop_pose的初值，结合继承过来的匹配点measurements_old_norm，再传回当前窗口中优化，problem.AddResidualBlock(f, loss_function, para_Pose[start], retrive_data_vector[k].loop_pose, para_Ex_Pose[0], para_Feature[feature_index]);，得到优化后的loop_pose。如果优化后的loop_pose相对对应帧的位姿relative_yaw小于阈值，则认为回环正确。而优化后的loop_pose相对回环帧原来的位姿，为relocalize_r和relocalize_t。
在vins-mono的新版本中，新增加了relocalize_r、relocalize_t，其作用是，在大回环起作用的间隙，用relocalize_r、relocalize_t来对位姿进行及时的修正，以更好地保证输出位姿的准确性，以及关键帧输入到关键帧数据库里时的位姿的准确性。因为以前是要等回环帧的对应帧滑出窗口，大回环优化后，才对这两个位姿进行校正的，而现在可以更及时地修正这些位姿，如果有地方想要最快速地得到准确的位姿的话。new KeyFrame(estimator.Headers[WINDOW_SIZE - 2], vio_T_w_i, vio_R_w_i, cur_T, cur_R, KeyFrame_image, pattern_file);这里面的vio_T_w_i是回环优化时的计算前后关键帧的相对位置时用的，所以用的还是窗口中的位姿。而cur_T，也就是T_w_i，是表示校正后的位姿，在输入的时候，会根据relocalize_r校正，大回环优化后，还再校正关键帧数据库里的所有的关键帧位姿。relocalize_r、relocalize_t也是很巧妙的方法，因为它们是根据回环帧和对应帧的图像的相对位姿算出来的回环偏移，其实大回环优化之后得到的回环偏移correct_t，和这个回环偏移relocalize_t，应该相差不大。大回环主要是优化环中间的那些关键帧的位姿，大回环的主要目的在于修正关键帧图PoseGraph。所以，relocalize_r、relocalize_t一开始就很接近最终大回环优化后的回环偏移correct_t。relocalize_t是把回环帧放到当前窗口下优化，算出来的与原来的偏移；correct_t是大回环优化后的对应帧位姿与它原来的位姿的偏移。correct_t准确但计算慢，relocalize_t计算快速且较准确。
这里的回环检测，是每3个关键帧检测一帧，相当于是跳两帧。这跟回环检测的速度，和实际关键帧生成的速度，对比有关。因为回环检测的速度总是慢于关键帧生成的速度，所以为了保持回环检测的关键帧不落后于时间，只能跳帧检测。ORBSLAM里面也是这样，但ORBSLAM里面的回环检测判断标准是，一段时间内的关键帧都能匹配上回环，所以ORBSLAM的策略是拿一段时间的关键帧来进行检测。ORBSLAM的回环检测程序，Sleep一段时间，在Sleep的这段时间，收集关键帧，然后开始工作，只针对收集的这些关键帧。工作时，不收集新的关键帧，都跳过。处理完这些关键帧后，又Sleep。
因为回环检测的速度总是慢于关键帧生成的速度，所以为了保持回环检测的关键帧不落后于时间，只能跳帧检测。
窗口里，每3个关键帧，送一个到关键帧数据库里。关键帧数据库里面的每一帧都跟之前的进行检测，看是否有回环。回环检测用的是DBow，这个关键帧上面的用FAST找出来的新的特征点和它在之前被光流跟踪到的特征点，提取描述子，与历史描述子匹配。这帧的描述子以及对应的特征点，跟历史上的描述子以及对应的特征点进行匹配，得到匹配上的特征点。
如果有回环，就等这个对应帧从窗口里滑出，再回环闭环。
找出回环最早开始的帧，然后把这帧的位姿设为固定。
回环闭环的约束条件是，与优化前的相对位姿不能差太大，每帧与前5帧的相对位姿。回环帧和对应帧的相对位姿的权重是5。回环闭环里面，优化的都是4自由度的姿态，回环帧与闭环帧，每帧与它的前5帧的相对姿态。
优化完后，在最后一个对应帧那里，再把世界坐标系也转换一下，然后把剩下的关键帧都转换一下。
回环闭环优化部分的测量值是，回环帧与对应帧的基于图像算出的相对4自由度姿态，就是relative_t和relative_yaw，就是回环帧的loop_pose在窗口中优化后，相对窗口中的对应帧的位姿。每帧图像与它前5帧的相对4自由度姿态。约束为，预测值和测量值之间的差。与此有关的自变量是，每帧图像的4自由度位姿。就像一个项链一样，一串地拉过来。
注意的是，回环帧与对应帧的基于图像算出的相对4自由度姿态的权重是5，为了平衡每帧图像与它前5帧的相对4自由度姿态。对应帧的前后对它的拉力要相同。
假设是第0帧和第m帧回环闭环了。
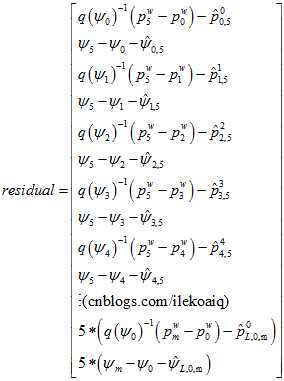
在这里，究竟是使用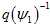
还是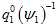
，我认为是一样的。前者是把下一帧相机的原点转换到上一帧相机的yaw角的水平坐标系下，以此为测量值，预测值与测量值的残差，关于yaw角求导。后者是把把下一帧的相机的原点转换到上一帧的坐标系下，预测值与测量值的残差，关于yaw角求导。但这里的yaw角都是指在水平世界坐标系里面的yaw角。最终优化的结果应该是一样的。像这种，只是把残差从一个直角坐标系转换到另外一个直角坐标系，结果应该是一样的。但是，如果是另外一些转换，那结果就可能不一样了，比如非直角坐标系，各维度的有不同的缩放尺度，或者维度变换，那样子的话，优化结果就会不一样。
这里使用程序里面的表示，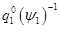
。程序里面没有求雅克比，而是用自动求导的方法。
回环检测之后的处理，非常有创新点。一般的，回环检测之后，是要根据回环检测结果，把窗口关键帧的位姿都转换掉。但实际上，是可以不管窗口里面的关键帧的，可以认为窗口里面的关键帧的世界坐标系相对真实的世界坐标系发生了偏移和转换。只需要在输出位姿的时候，乘以这个转换就可以了，窗口里面的位姿还是原来的位姿。这样子，就可以避免对窗口的位姿进行大幅度调整，也不需要重新计算雅克比，协方差矩阵。输出的结果是应用所需要的，修正过的结果。
为了输出最新的位姿，需要把新缓存进来的IMU数据也都积分起来。更新实时的最新的位姿。然后，每新进来一个IMU数据，就在之前的基础上预测一下。因为IMU数据都是在载体坐标系的，所以，可以先在窗口的坐标系里积分，然后最后再转换到真实的世界坐标系，也可以直接把坐标转换到真实的世界坐标系，然后再积分。最后都是得到在真实的世界坐标系里面的位姿，然后每新进来一个IMU数据，就在之前的基础上预测一下。这两种方法是一样的。
您觉得，本文值多少？
标签：第一步 深度 总结 使用 缓存 元素 eigen 统一 球面
原文地址：https://www.cnblogs.com/ilekoaiq/p/8836970.html
