标签:连续 才有 png dad variables 分析 nova 参与 lines
一、问题与数据
研究者想知道短期(2周)高强度锻炼是否会减少C反应蛋白(C-Reactive Protein, CRP)的浓度。
研究者招募了12名研究对象,并让研究对象参与两组试验:对照试验和干预试验。在对照试验中,研究对象照常进行日常活动;在干预试验中,研究对象每天进行45分钟的高强度锻炼,每组试验持续2周,两组试验中间间隔足够的时间。
CRP的浓度在每组试验中共测量了3次:试验开始时的CRP浓度、试验中的CRP浓度(1周)和试验结束时的CRP浓度(2周)。这三个时间点代表了受试者内因素“时间”的三个水平,因变量是CRP的浓度,单位是mg/L。
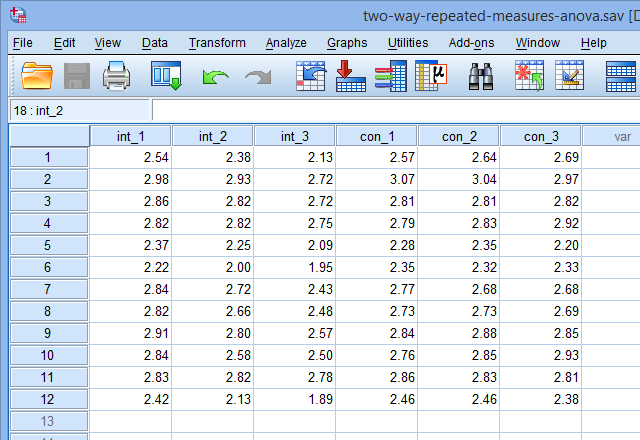
con_1、con_2和con_3分别代表对照试验开始时、对照试验中和对照试验结束时研究对象的CRP浓度,int_1、int_2和int_3分别代表干预试验开始时、干预试验中和结束时研究对象的CRP浓度。部分数据如下:
二、对问题的分析
使用两因素重复测量方差分析(Two-way Repeated Measures Anova)进行分析时,需要考虑5个假设。
对研究设计的假设:
假设1:因变量唯一,且为连续变量;
假设2:有两个受试者内因素(Within-Subject Factor),每个受试者内因素有2个或以上的水平。
注:在重复测量的方差分析模型中,对同一个体相同变量的不同次观测结果被视为一组,用于区分重复测量次数的变量被称为受试者内因素,受试者内因素实际上是自变量。
对数据的假设:
假设3:受试者内因素的各个水平,因变量没有极端异常值;
假设4:受试者内因素的各个水平,因变量需服从近似正态分布;
假设5:对于受试者内因素的各个水平组合而言,因变量的方差协方差矩阵相等,也称为球形假设。
三、思维导图
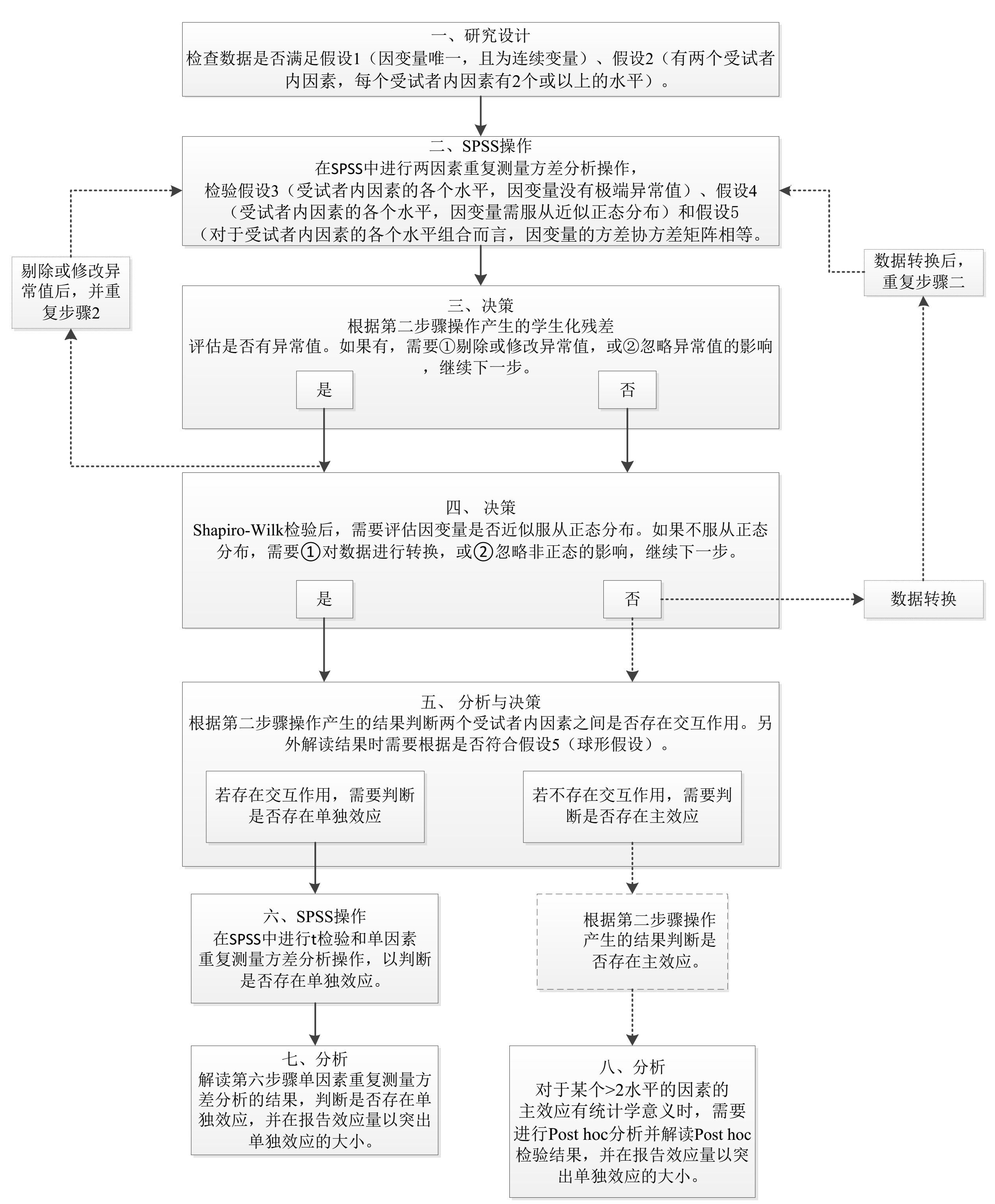
四、SPSS操作-两因素重复测量方差分析的操作
1. 在主菜单下点击Analyze > General Linear Model > Repeated measures...,如下图所示:
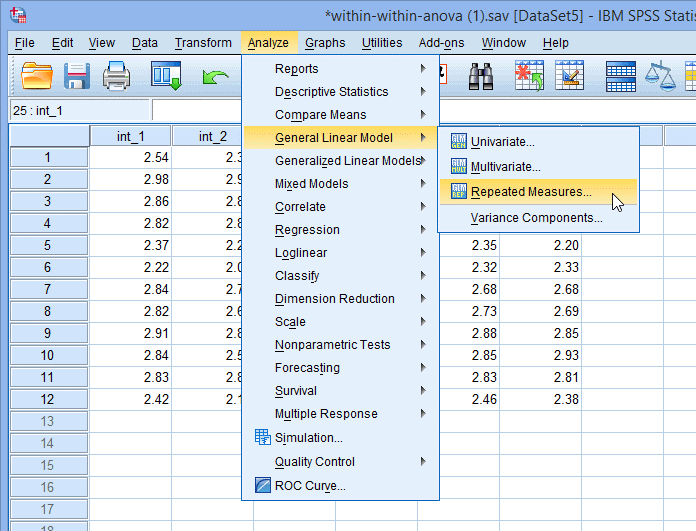
2. 出现Repeated Measures Define Factor(s)对话框,如下图所示:
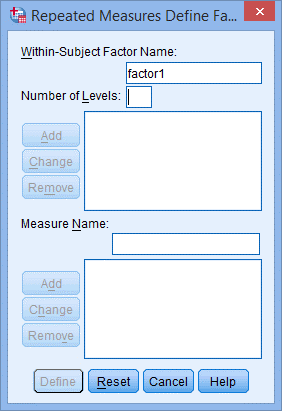
3. 在Within-Subject Factor Name:中将“factor1”更改为treatment,因为研究对象共进行了2组试验,在Number of Levels:中填入2;
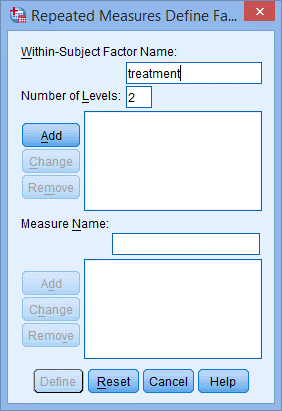
4. 点击Add,出现下图:
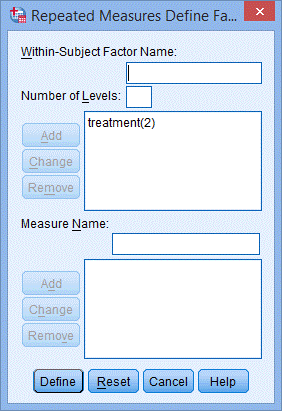
5. 在Within-Subject Factor Name:中填入time,因为研究对象的CRP水平在每组试验中共测量了3次,在Number of Levels:中填入3,点击Add;
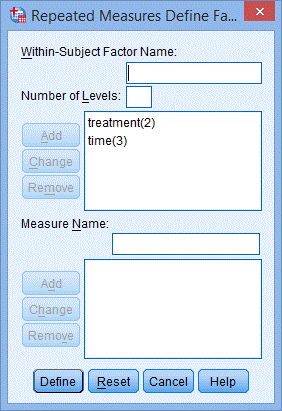
6. 点击Define,出现下图Repeated Measures对话框;
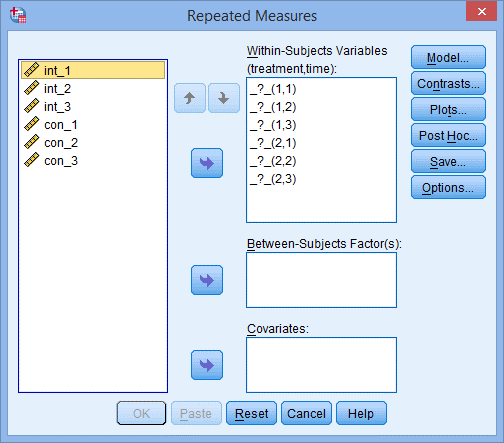
7. 如下图所示,Within-Subjects Variables后面的括号内是受试者内因素的名字,将左侧六个变量均选入右侧框中,如下图所示:
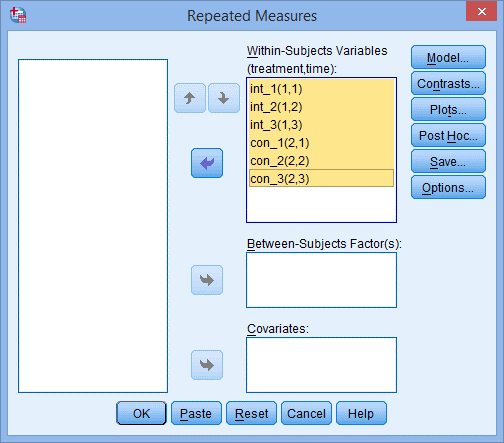
8. 点击Plots,出现Repeated Measures: Profile Plots 对话框,如下图所示:
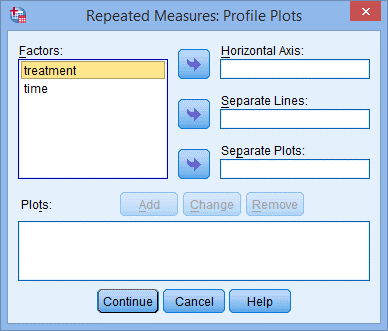
9. 将time选入Horizontal Axis:框中,将treatment选入Separate Lines:框中;
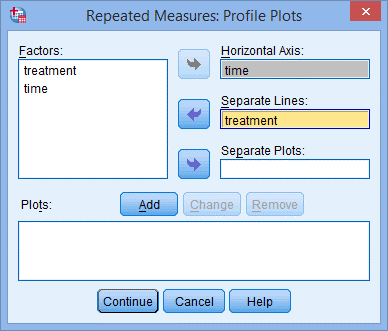
10. 点击Add,出现下图,点击Continue;
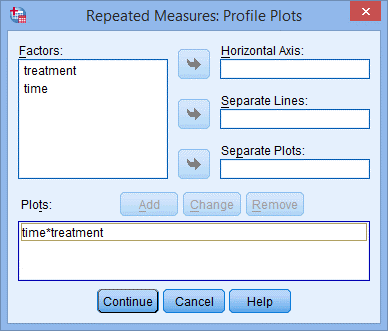
11. 点击Save,出现Repeated Measures: Save对话框;
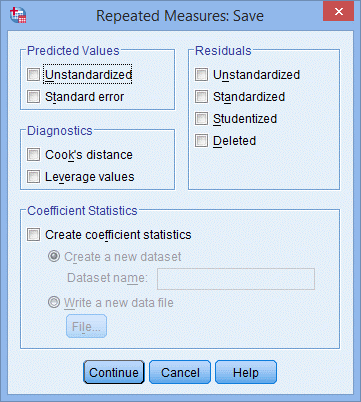
12. 在Residuals下方选择Studentized,如下图所示,点击Continue;
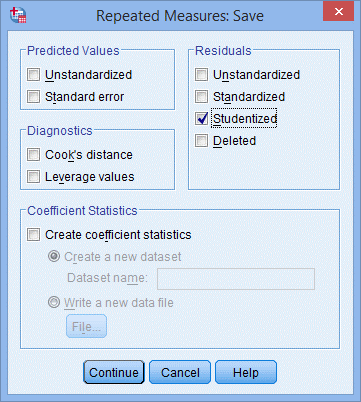
13. 点击Options,出现Repeated Measures: Options对话框;
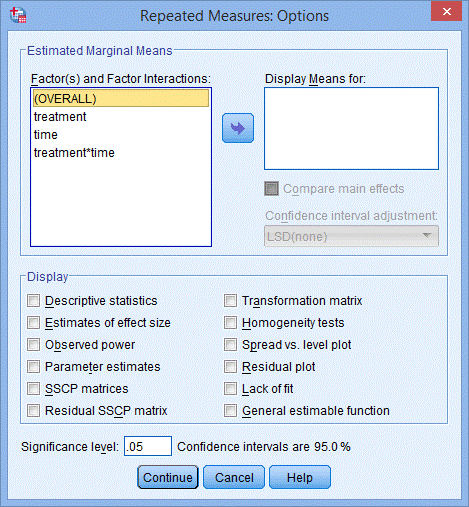
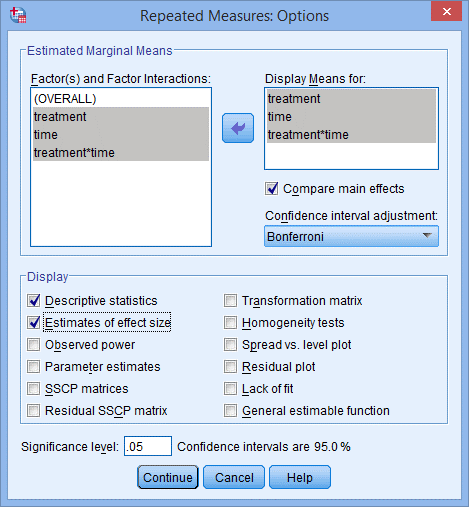
14. 将treatment、time和treatment*time选入Display Means for:中,下方Compare main effects为勾选状态,在Confidence interval adjustment:下选择Bonferroni,在Display下方勾选Deive statistics 和Estimates of effect size,点击Continue,点击OK。
五、对假设的判断
那么,用Two-way Repeated Measures Anova分析时,如何考虑和处理这5个假设呢?
由于假设1-2都是对研究设计的假设,需要研究者根据研究设计进行判断。本例中因变量为CRP浓度,是连续变量,符合假设1:因变量唯一,且为连续变量。
共有2个受试者内因素:干预因素(两个水平:1个水平为“干预”,另一个水平为“对照”)和时间因素(3个水平:试验开始时、试验中和试验结束时),符合假设2:有两个受试者内因素(Within-Subject Factor),每个受试者内因素有2个或以上的水平。
2个受试者内因素干预因素(两个水平:1个水平为“干预”,另一个水平为“对照”)和时间因素(3个水平:试验开始时、试验中和试验结束时),共形成了6个“处理”组。
下面我们主要对数据的假设3-5进行判断。
(一) 假设3:受试者内因素的各个水平,因变量没有极端异常值;
1. 通过学生化残差判断异常值
在上述操作中我们选择了保存Studentized residuals,就是学生化残差,一般认为观测的学生化残差超过±3(标准差)时为异常值。进行上述操作后,我们在数据主页面可以看到产生了6个新变量。
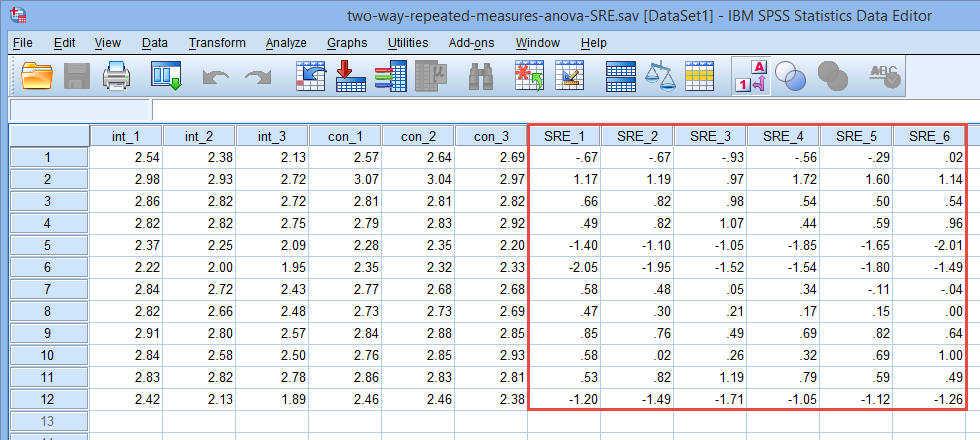
注:残差是指实际观察值与估计值(拟合值)之间的差,学生化残差是残差中一种。
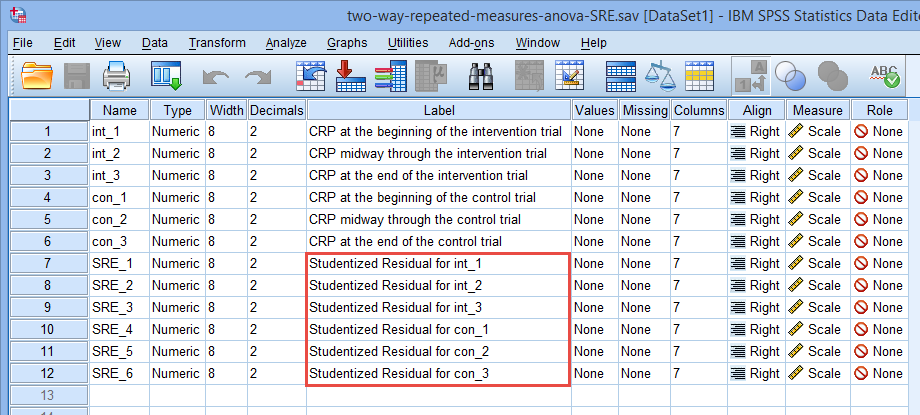
点击数据下方的Label,可以看到新产生的6个变量对应的意义,如下图所示,分别是int_1、int_2、int_3、con_1、con_2和con_3的学生化残差。
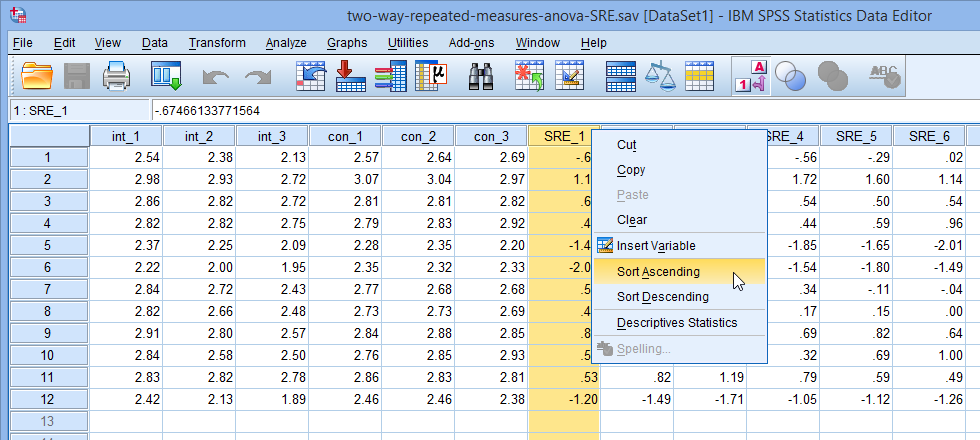
要判断观测是否为离群值,可以查看学生化残差是否超过±3的范围。在数据页面对新生变量进行排序,右击SRE_1,选择Sort Ascending,将SRE_1按照从大到小的顺序排列。
如下图所示,SRE_1最小值为-2.05,最大值为1.17,没有超过±3的范围。
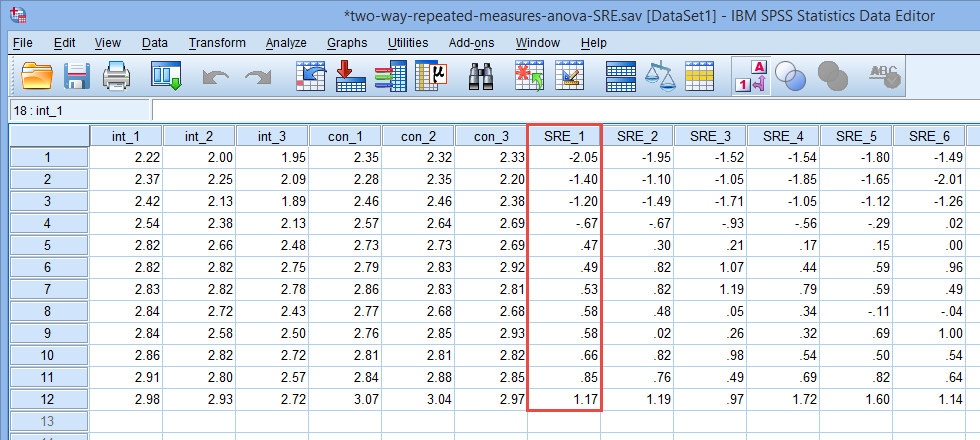
用同样的方法可以对其他5个新生变量进行检验。如果没有发现异常值,可以这样报告:通过用学生化残差是否超过±3的方法没有发现异常值;如果发现异常值,可以这样报告:通过用学生化残差是否超过±3的方法,发现一个异常值,该观测的学生化残差为3.83。
2. 异常值的处理
(1) 导致数据中存在异常值的原因有3种:
1) 数据录入错误:首先应该考虑异常值是否由于数据录入错误所致。如果是,用正确值进行替换并重新进行检验;
2) 测量误差:如果不是由于数据录入错误,接下来考虑是否因为测量误差导致(如仪器故障或超过量程),测量误差往往不能修正,需要把测量错误的数据删除;
3) 真实存在的异常值:如果以上两种原因都不是,那最有可能是一种真实的异常数据。这种异常值不好处理,但也没有理由将其当作无效值看待。目前它的处理方法比较有争议,尚没有一种特别推荐的方法。
需要注意的是,如果存在多个异常值,应先把最极端的异常值去掉后,重新检查异常值情况。这是因为有时最极端异常值去掉后,其他异常值可能会回归正常。
(2) 异常值的处理方法分为2种:
1) 保留异常值:
① 因变量转换成其他形式;
② 将异常值纳入分析,并坚信其对结果不会产生实质影响。
2) 剔除异常值:
直接删除异常值很简单,但却是没有办法的办法。当我们需要删掉异常值时,应报告异常值大小及其对结果的影响,最好分别报告删除异常值前后的结果。而且,应该考虑有异常值的个体是否符合研究的纳入标准。如果其不属于合格的研究对象,应将其剔除,否则会影响结果的推论。
(二) 检验假设4:受试者内因素的各个水平,因变量需服从近似正态分布
尽管有一系列方法可以检验正态性,我们这里通过Shapiro-Wilk‘s检验学生化残差的正态性。
1. 在主菜单点击Analyze > Deive Statistics > Explore...,如下图:
2. 出现Explore对话框,将新产生的6个学生化残差选入Dependent List,点击Plots;
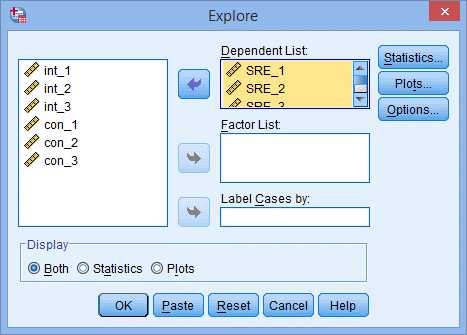
3. 出现下图Plots对话框;
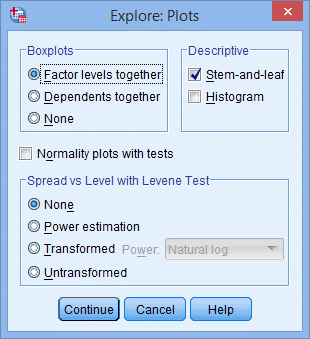
4. 在Boxplots下选择None,去掉Deive下Stem-和-leaf,选择Normality plots with tests,点击Continue,点击OK。
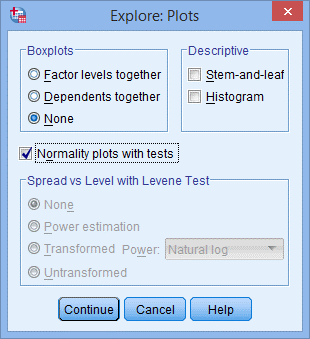
5. 对于样本量较小(<50例)的研究,推荐使用Shapiro-Wilk方法检验正态性。当P<0.05时,认为不是正态分布。本例中,除了SRE_1的P=0.022<0.05之外,P均大于0.05,说明SRE_2~SRE_6均服从正态分布。本例中,我们假设SRE_1违反正态分布的程度不严重,不需要对数据进行转换。
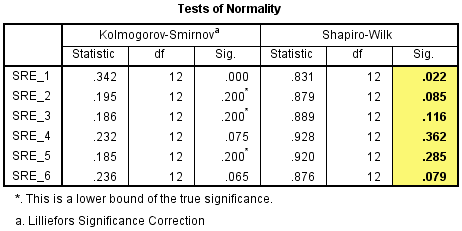
可以这样报告:通过Shapiro-Wilk‘s 检验学生化残差的正态性,除了干预试验开始时的CRP浓度外,其他测量的CRP浓度都服从正态分布。
6. 如果数据不服从正态分布,可以有如下3种方法进行处理:
(1) 数据转换:对转换后呈正态分布的数据进行单因素方差分析。当各组因变量的分布形状相同时,正态转换才有可能成功。对于一些常见的分布,有特定的转换形式,但是对于转换后数据的结果解释可能比较复杂。
(2) 直接进行分析:由于单因素重复测量方差分析对于偏离正态分布比较稳健,尤其是在各组样本量相等或近似相等的情况下,而且非正态分布实质上并不影响犯I型错误的概率。因此可以直接进行检验,但是结果中仍需报告对正态分布的偏离。
(3) 检验结果的比较:将转换后和未转换的原始数据分别进行单因素重复测量方差分析,如果二者结论相同,则再对未转换的原始数据进行分析。
六、结果解释
在结果解释之前,我们需要先明确几个概念:单独效应、主效应和交互作用。
单独效应(simple effect):指其他因素的水平固定时,同一因素不同水平间的差别。例如,当A因素固定在第1个水平时,B因素的单独效应为20;当A因素固定在第2个水平时,B因素的单独效应为24。
主效应(main effect):指某一因素的各水平间的平均差别。例如,当A因素固定在第1个水平时,B因素的单独效应为20;当A因素固定在第2个水平时,B因素的单独效应为24。平均后得到B因素的主效应(20+24)/2=22。
交互作用(interaction):当某因素的各个单独效应随另一因素变化而变化时,则称这两个因素间存在交互作用。
为了更方便理解交互作用的概念,可以看一下下图中的举例。当两条线是平行时,交互作用没有统计学意义;当两条线不平行,即使没有在数据中有交叉点,交互作用也存在。
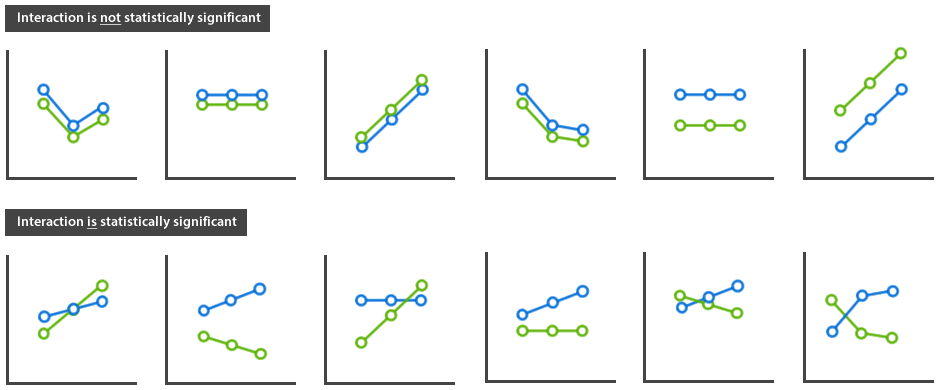
当存在交互作用时,单独分析主效应的意义不大,需要逐一分析各因素的单独效应;当不存在交互作用时,说明两因素的作用效果相互独立,逐一分析各因素的主效应即可。
(一) 基本描述
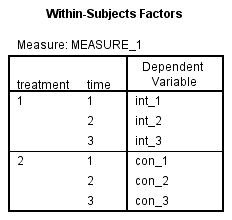
1. SPSS首先会给出Within-Subjects Factors表,该表提示了两个受试者内因素treatment和time各个水平对应的标签,在后面的表格中会用到。
2. Deive Statistics表给出了int_1、int_2、int_3、con_1、con_3和con_3的均值,标准差和例数。
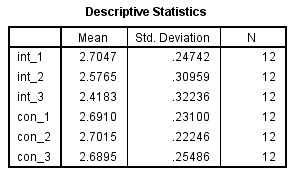
干预试验开始时、干预试验中和干预试验结束时研究对象的CRP浓度干预试验分别为2.70 ± 0.25 mg/L、2.58 ± 0.31 mg/L和2.42 ± 0.32 mg/L,对照试验开始时、对照试验中和对照试验结束时研究对象的CRP浓度对照试验分别为2.69 ± 0.23 mg/L、2.70 ± 0.22 mg/L和2.69 ± 0.25 mg/L。
在该表中可以看到,随着时间推移,对照试验三个时间点的CRP浓度相似,而干预试验三个时间点的的CRP浓度则有所下降。
3. treatment*time表中没有再出现int_1、int_2、int_3、con_1、con_3和con_3的变量名,而是给出了对应的3个时间点的标签。该表中给出了int_1、int_2、int_3、con_1、con_3和con_3的均值、标准误和均值的95%置信区间。
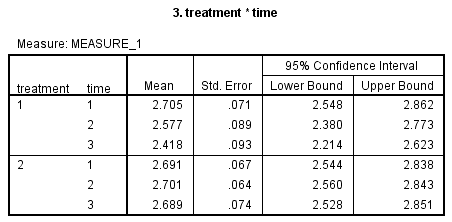
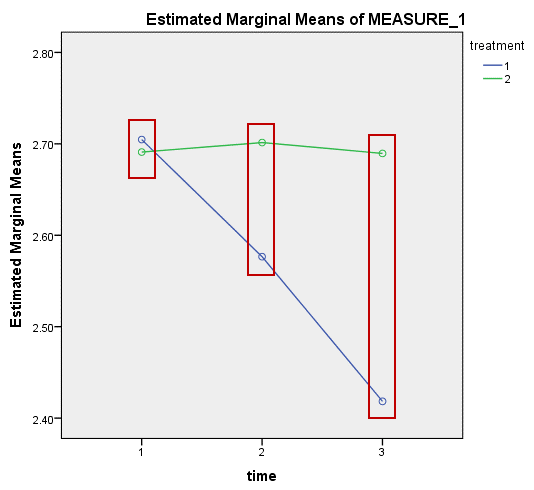
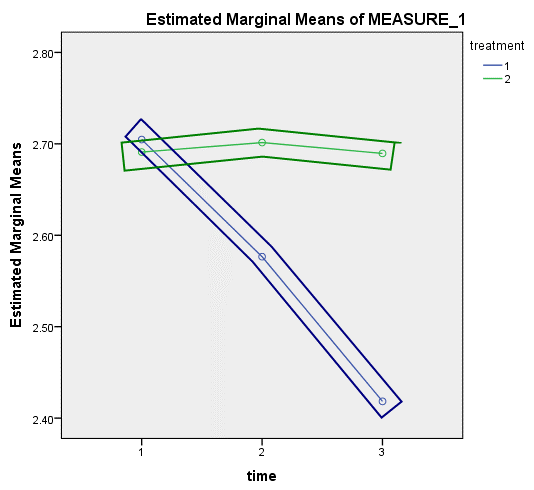
4. Estimated Marginal Means of MEASURE_1给出了对照试验和干预试验三个时间点CRP均值的折线图。
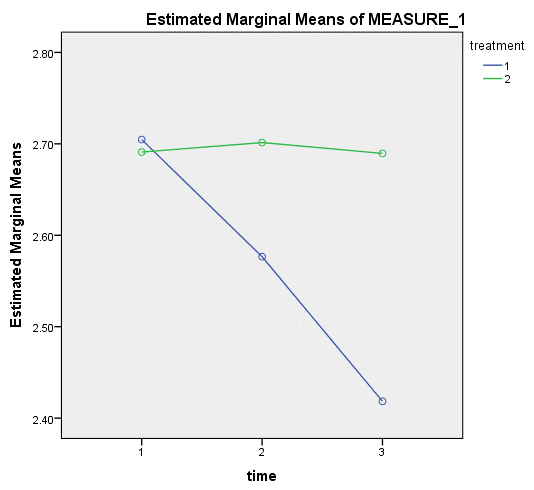
可以看到,对照试验和干预试验在开始时的CRP浓度相似,随着时间推移,干预试验中研究对象的CRP浓度呈下降趋势,而对照试验中研究对象的CRP浓度变化不大。从该图中看到,两条线不平行,提示两个受试者内因素存在交互作用。
(二) 球形假设的检验结果
1. 在判断两个受试者内因素是否存在交互作用前,需要先判断是否符合球形假设。在Mauchly‘s Test of Sphericity表中,给出了球形假设的检验结果。

如果P<0.05,则球形假设不满足;如果P>0.05,则满足球形假设。本例中,交互项treatment*time的χ2=5.270,P=0.072,所以对于交互项,因变量满足球形假设。
2. 当违背了球形假设条件时,需要进行epsilon (ε)校正。如下图突出显示,SPSS共用了三种方法进行校正,分别为:Greenhouse-Geisser、Huynh-Feldt和Lower-bound。

在实际应用中,只用Greenhouse-Geisser和Huynh-Feldt两种方法,这两种方法计算得到的epsilon (ε)的值越低,说明违反球形假设的程度越大,当epsilon (ε)=1时,说明完美的服从了球形假设。
Maxwell & Delaney (2004)建议当epsilon (ε)<0.75时,使用Greenhouse-Geisser方法校正。其他统计学家建议当epsilon (ε)>0.75时,使用Huynh-Feldt方法校正。
3. 满足球形假设的结果
上述交互项满足球形假设,我们下面需要看交互项对因变量的影响是否有统计学意义。在Tests of Within-Subjects Effects表中,如果P>0.05,则表示交互项无统计学意义(本例中,P值显示为0.000,不代表P值实际为0,而是表示P<0.001)。
如表中突出显示的内容所示,在Sphericity Assumed行,treatment和time的交互作用具有统计学意义,F(2, 22)=30.157,P<0.001。
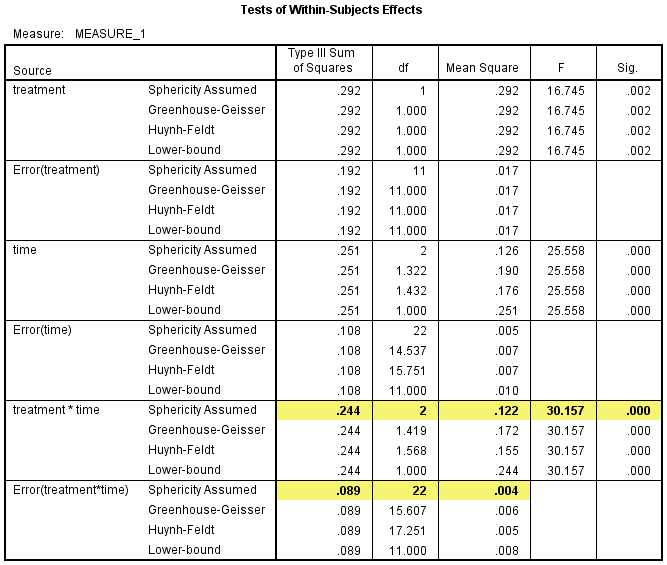
4. 不满足球形假设的结果
当不满足球形假设时,可以采用Greenhouse & Geisser方法进行校正,如下表中突出显示的内容。
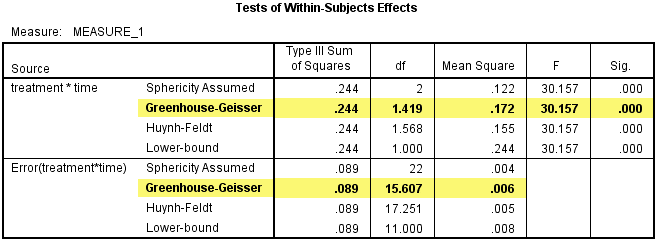
可见,交互项的自由度(df)由原来符合球形假设时的2变成了1.419,误差项的自由度由原来的22变成了15.607,均方(Mean Square)由原来的0.122变成了0.172,treatment和time的交互作用具有统计学意义,F(1.419, 15.607) = 30.157,P<0.001。
(三) 交互作用存在时的分析步骤
当交互作用有意义时,单独分析主效应的意义不大,需要逐一分析不同时间水平干预试验和对照试验中研究对象CRP浓度的差异,即各受试者内因素的单独效应。
1. treatment的单独效应
检验treatment的单独效应是指在不同时间水平比较干预试验和对照试验中研究对象CRP浓度的差异,需要三次单独的比较,如下图所示。
受试者内因素time有三个水平,所以需要做三次比较。需要做的3个比较分别为:int_1与con_1、int_2与con_2和int_3与con_3。
(1) SPSS操作
1) 在主菜单下点击Analyze > General Linear Model > Repeated measures...,如下图所示:
2) 出现Repeated Measures Define Factor(s)对话框,如下图所示:
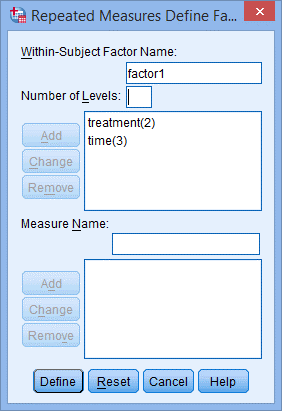
3) 单击time(3),点击Remove按钮,在Number of Levels:只剩treatment(2),如下图所示:
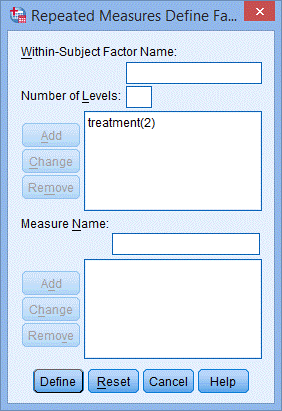
4) 点击Define,出现下图Repeated Measures对话框;
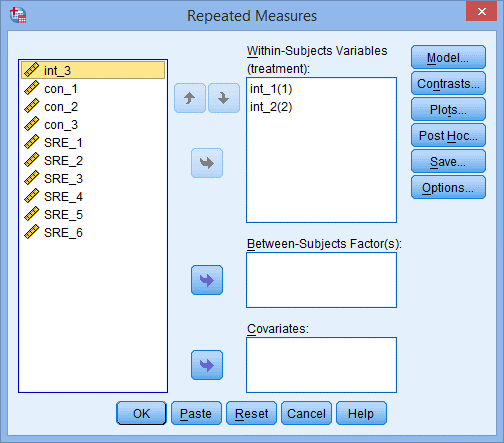
5) 如下图所示,Within-Subjects Variables后面的括号内是受试者内因素的名字,将左侧int_1和con_1变量均选入右侧框中,如下图所示:
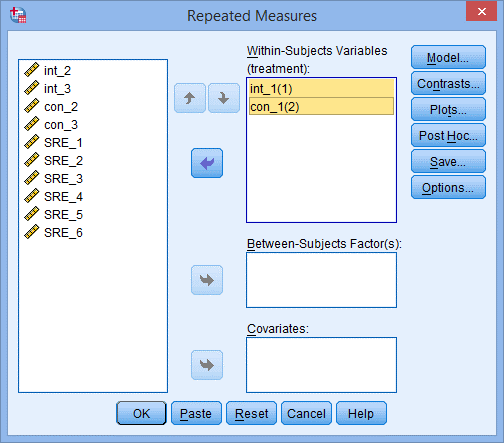
6) 点击Options,出现Repeated Measures: Options对话框,如下图所示:
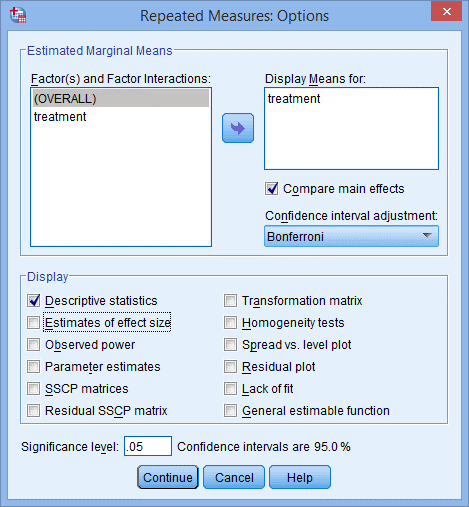
7) 去掉Display下方勾选Deive statistics,点击Continue,点击OK。
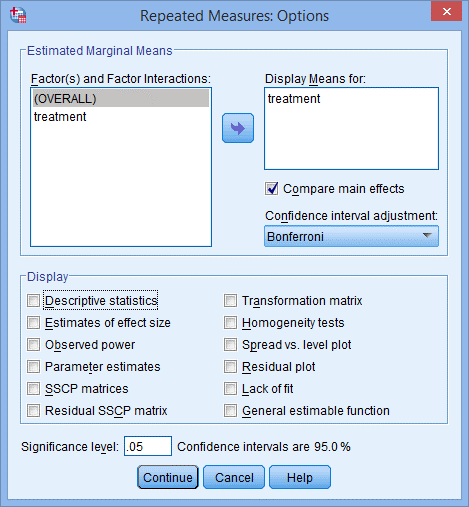
8) 第二个treatment的单独效应重复上述操作,将步骤5中将int_2和con_2选入右侧框中;第三个treatment的单独效应重复上述操作,将步骤5中将int_3和con_3选入右侧框中。
(2) treatment单独效应的结果
1) int_1和con_1的比较结果
当只有两个组比较时,不需要检验球形假设。Tests of Within-Subjects Effects表是对因变量进行一元方差分析的结果。P<0.05时,自变量对因变量的影响存在统计学意义;P≥0.05时,自变量对因变量的影响不存在统计学意义。
该表给出了研究开始时treatment对因变量的单独效应,treatment对CRP浓度的影响不具有统计学意义,F(1, 11)=0.402, P=0.539。
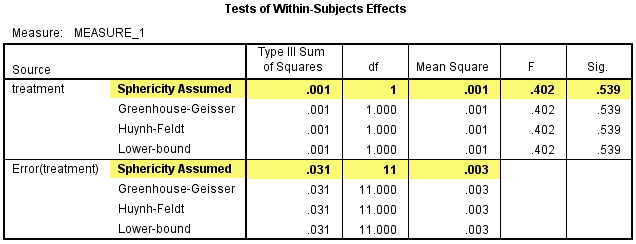
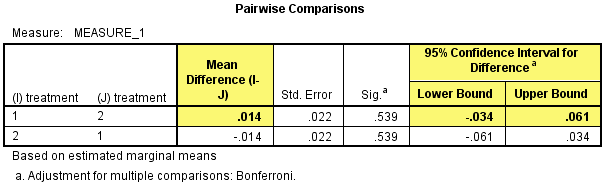
然后在Pairwise Comparisons表中看int_1和con_1的两两比较结果,在研究开始时干预试验中研究对象的CRP浓度比对照试验的高0.14(95%置信区间:-0.034 - 0.061)mg/L,但差异不具有统计学意义,P=0.539。
2) int_2和con_2的比较结果
Test of Within-Subjects Effects表给出了研究中期treatment对因变量的单独效应,treatment对CRP浓度的影响具有统计学意义, F(1, 11) =10.434,P=0.008。
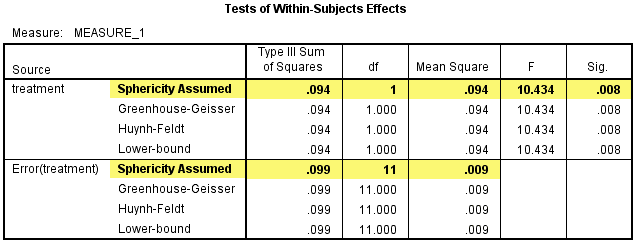
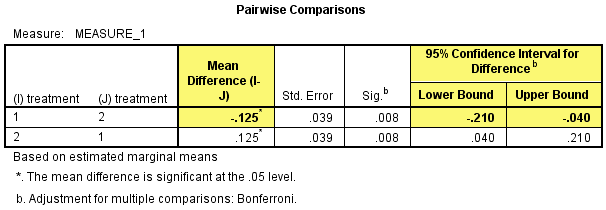
然后在Pairwise Comparisons表中看int_2和con_2的两两比较结果,在研究中期时干预试验中研究对象的CRP浓度比对照试验的低0.125(95%置信区间:-0.210 - 0.040)mg/L,差异具有统计学意义,P=0.008。
3) int_3和con_3的比较与上述相似,在此不做赘述。
注意:有些学者和统计学家推荐在进行多个单独效应的比较时进行校正。常用的方法是对显著性水平进行Bonferroni校正:用现有的显著性水平除以单独效应的个数。本例中,treatment的单独效应有3个,所以校正后的显著性水平α=0.05÷3=0.0167。
2. time的单独效应
相似的,检验time的单独效应是指在treatment的不同组中比较时间因素的差异。受试者内因素treatment有两个水平,所以需要做两次比较,如下图所示。做这些比较与做2次单因素重复测量方差分析相同,需要做的2个比较分别为:int_1、int_2与int_3和con_1、con_2与con_3。time的单独效应与上述treatment的单独效应SPSS操作相似,在此不做赘述。
(1) 对照试验中time的单独效应
1) 由于time的单独效应是比较3个水平,所以需要判断是否符合球形假设。如下图所示,P=0.053,大于0.05,所满足球形假设。

2) 然后看Test of Within-Subjects Effects表,该表给出了对照试验time的单独效应,在对照试验中时间因素对CRP浓度的影响没有统计学意义,F(2, 22) =0.182,P=0.835。由于对照试验中时间因素对CRP浓度的影响没有统计学意义,所以不必在进行三个时间点的两两比较。
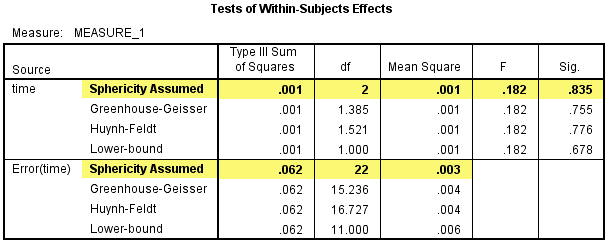
(2) 干预试验中time的单独效应
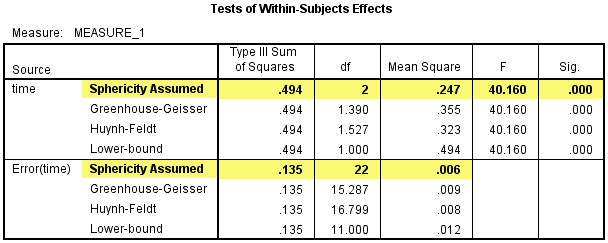
1) 由于time的单独效应是比较3个水平,所以需要判断是否符合球形假设。如下图所示,P=0.056,大于0.05,满足球形假设。

2) 然后看Test of Within-Subjects Effects表,该表给出了干预试验中time的单独效应,在干预试验中时间因素对CRP浓度的影响有统计学意义,F(2, 22) =40.160,P<0.001。
3) 下面是两两比较的结果。如下图所示,试验开始时的CRP浓度(2.70 ± 0.25 mg/L)与试验中期的CRP浓度(2.58 ± 0.31 mg/L)的差异具有统计学意义(P=0.002),差值为0.128(95%置信区间:0.052 - 0.205) mg/L;试验中期时的CRP浓度(2.58 ± 0.31 mg/L)与试验结束时的CRP浓度(2.42 ± 0.32 mg/L)的差异具有统计学意义(P<0.001),差值为0.158(95%置信区间:0.087 - 0.230) mg/L。
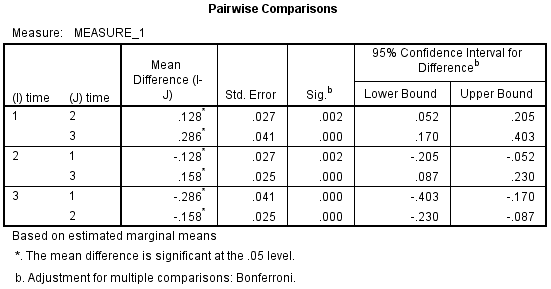
(四) 交互作用不存在时的分析步骤
当交互作用不存在时,需要解读两个受试者内因素(treatment和time)的主效应。如果>2水平的受试者内因素的主效应存在,需要后续进行两两比较。
1. treatment的主效应
1) 由于treatment只有两个水平(干预与对照),所以不需要检验是否符合球形假设。Test of Within-Subjects Effects表给出了treatment的主效应结果。检验treatment的主效应意味着检验无论在什么时间点上,CRP的浓度是否有差异。
在Test of Within-Subjects Effects表中,P<0.05时,自变量对因变量的影响存在统计学意义;P≥0.05时,自变量对因变量的影响不存在统计学意义。如下图突出显示所示,treatment对CRP浓度的主效应具有统计学意义,F(1, 11)=16.745,P=0.002。
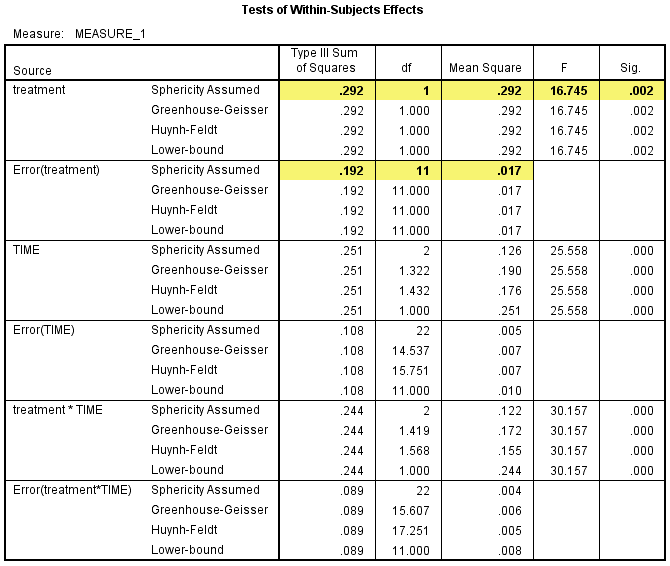
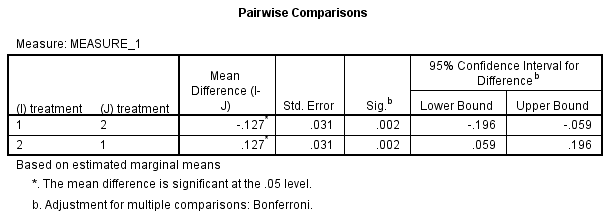
2) 下面是两两比较的结果。如下图Pairwise Comparisons表中所示,干预试验中研究对象的CRP浓度比对照试验的CRP浓度低0.127(95%置信区间:-0.196 ~ -0.059) mg/L,差异具有统计学意义,P=0.002。
2. time的主效应
1) 由于time的主效应是比较3个水平,所以需要判断是否符合球形假设。如下图所示,P=0.027(<0.05),所以不满足球形假设。可以看到Greenhouse-Geisser方法计算的Epsilon=0.661<0.75,所以后面需要解读Greenhouse-Geisser的结果。

2) Test of Within-Subjects Effects表给出了time主效应,时间因素对CRP浓度的影响具有统计学意义,F(1.322, 14.537) =25.558,P<0.001。由于时间因素对CRP浓度的影响具有统计学意义,所以需要进行三个时间点的两两比较。
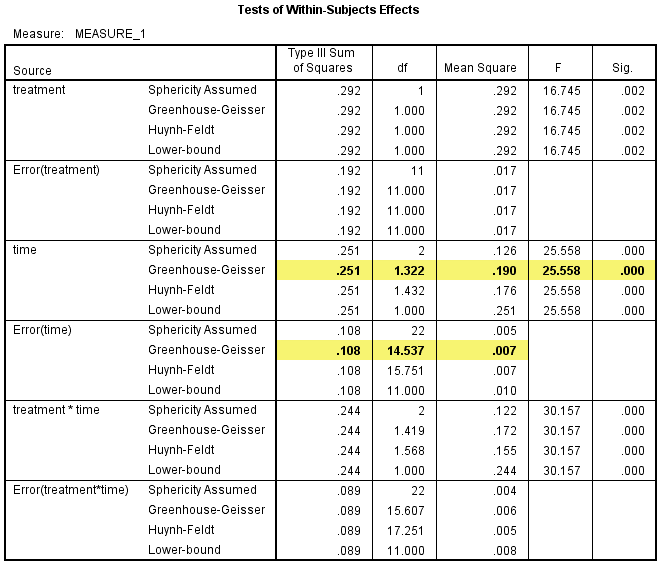
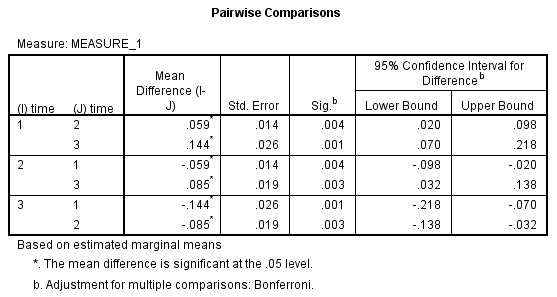
3) 下面是两两比较的结果。如下图所示,试验开始时的CRP浓度与试验中期的CRP浓度的差异具有统计学意义(P=0.004),差值为0.059(95%置信区间:0.020 - 0.098) mg/L,试验中期时的CRP浓度与试验结束时的CRP浓度的差异具有统计学意义(P=0.003),差值为0.085(95%置信区间:0.032 - 0.138) mg/L。
七、撰写结论
1. 当两受试者内因素间存在交互作用时
采用两因素重复测量方差分析方法,判断不同干预措施随着时间的变化对受试者CRP浓度的影响。通过对学生化残差的分析,经Shapiro-Wilk检验,各组数据服从正态分布(P>0.05);通过学生化残差是否超过±3倍的标准差判断,各组数据无异常值。经Mauchly‘s球形假设检验,对于交互项treatment*time,因变量的方差协方差矩阵相等(P>0.05)。
数据以均数±标准差的形式表示。treatment和time的交互作用对CRP浓度的影响有统计学意义,F(2, 22)=30.157,P<0.001。因此,对两个受试者内因素treatment和time进行单独效应的检验。
在试验开始时,对照试验(2.69 ± 0.23 mg/L)与干预试验(2.70 ± 0.25 mg/L)中研究对象的CRP浓度的差异不具有统计学意义,F(1, 11)=0.402,P=0.539。
在试验中期时,对照试验(2.70 ± 0.22 mg/L)与干预试验(2.58 ± 0.31 mg/L)中研究对象的CRP浓度的差异具有统计学意义,差值为0.13(95%置信区间:0.04 - 0.21) mg/L,F(1, 11)=10.434,P=0.008。
在试验结束时,对照试验(2.69 ± 0.25 mg/L)与干预试验(2.42 ± 0.32 mg/L)中研究对象的CRP浓度的差异也具有统计学意义,差值为0.27(95%置信区间:0.17 - 0.38) mg/L,F(1, 11)=32.069,P<0.001。
在对照试验中,对于受试者内因素time,因变量符合球形假设(P=0.053)。时间因素对CRP浓度的单独效应没有统计学意义,F(2, 22)=0.182,P=0.835。在干预试验中,对于受试者内因素time,因变量符合球形假设(P=0.056),时间因素对CRP浓度的单独效应有统计学意义,F(2, 22)=40.160,P<0.001。
干预试验开始时的CRP浓度(2.70 ± 0.25 mg/L)与干预试验中期的CRP浓度(2.58 ± 0.31 mg/L)的差异具有统计学意义(P=0.002),差值为0.128(95%置信区间:0.052 - 0.205) mg/L,干预试验中期时的CRP浓度(2.58 ± 0.31 mg/L)与干预试验结束时的CRP浓度(2.42 ± 0.32 mg/L)的差异具有统计学意义(P<0.001),差值为0.158(95%置信区间:0.087 - 0.230) mg/L。
2. 当两受试者内因素间不存在交互作用时
采用两因素重复测量方差分析方法,判断不同干预措施随着时间的变化对受试者CRP浓度的影响。通过对学生化残差的分析,经Shapiro-Wilk检验,各组数据服从正态分布(P>0.05);通过学生化残差是否超过±3倍的标准差判断,各组数据无异常值。经Mauchly‘s球形假设检验,对于交互项treatment*time,因变量的方差协方差矩阵相等(P>0.05)。
数据以均数±标准差的形式表示。treatment和time的交互作用对CRP浓度的影响无统计学意义,F(2, 22)=1.026,P=0.258。因此,需要解读两个受试者内因素 (treatment和time)的主效应。如果>2水平的受试者内因素的主效应存在,需要后续进行两两比较。
treatment对CRP浓度的主效应具有统计学意义,F(1, 11)=16.745,P=0.002。干预试验中研究对象的CRP浓度比对照试验的CRP浓度低0.127(95%置信区间:-0.196 ~ -0.059)mg/L,差异具有统计学意义,P=0.002。
时间因素对CRP浓度的影响具有统计学意义,F(1.322, 14.537) =25.558,P<0.001。因时间因素有3个水平,故进行两两比较。试验开始时的CRP浓度与试验中期的CRP浓度的差异具有统计学意义(P=0.004),差值为0.059(95%置信区间:0.020 - 0.098) mg/L,试验中期时的CRP浓度与试验结束时的CRP浓度的差异具有统计学意义(P=0.003),差值为0.085(95%置信区间:0.032 - 0.138) mg/L。
标签:连续 才有 png dad variables 分析 nova 参与 lines
原文地址:https://www.cnblogs.com/suho/p/8849693.html