标签:style blog http color sp 2014 c log r
看了《浅谈数形结合思想在信息学竞赛中的应用》
刚开头说了一个数形结合的例子,简单证明renay引理.
renay引理说的是有一个数列{an}满足数列中所有数的和为1,则数列中有且仅有一个循环数列(可以把初始序列看成是一个环,从任意一处拆开形成一个新的序列,长度为n,就叫做循环数列),满足任意部分和大于0(部分和就是a1,a1+a2,a1+a2+a3...).据说这个引理和catalan数有很大的关系.这里还是继续写写对斜率dp的理解吧.
文中的题目大意:
读入一列正数,a1,a2,a3...an,以及一个F。定义ave(i,j)=(ai+...+aj)/(j-i+1) i<=j 求一个ave最大且满足这列数的长度大于等于F. F<=N<=10^5
暴力做法就是枚举所有长度大于F的子序列,求出他们的ave(i,j)然后选出一个最大值.
而斜率优化需要把这个这个ave(i,j)换成一个斜率的形式.记s(i)=a1+a2+...+ai
则ave(i,j)=(s(j)-s(i-1))/(j-i+1) 这个就是斜率的形式.
论文中描述的当(j,s(j))点作为一个上凸点的时候是可以删除的(意思是后面的点和这个j点连线不可能成为最优解.),个人觉得其实画个图还是比较好理解的.把所有的点按照x从小到大排序,ps:这样,暴力就是,i<j时,每加入一个j点,就和在j之前的所有点i求一次ave(i,j),然后更新最大值.
在暴力的过程中发现,如果存在p1(i,s(i)),p2(k,s(k)),p3(j,s(j))三个点,且p2点在p1p2连线的上凸点,那么这里要证明的就是在p3后面加入的任何一个点px与p2的连线都不能成为最优解.所以p2这个点在后来加入的所有点中就没有必要求一次ave(i,j)(但是并不意味着p1p2这个ave要被删除).
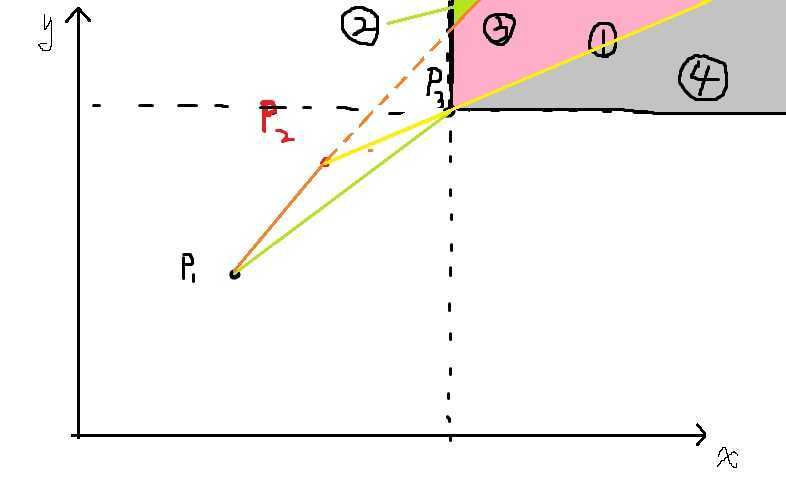
针对这个题画了一个图,很清楚的看到斜率优化,①代表的是下一个点有可能出现的区域,那么假设新加入的点为px(x,s(x)),首先它只能在①区域中,那么如果p2点有用(即不剔除),那么pxp2必须有可能比pxp1优(条件1),而且pxp2也必须有可能比pxp3更优(条件2).那么要满足第一个条件,px只能出现在②区域.而满足第二个条件,px又不能出现在③区域,而③区域是包含②区域的,所以证明了px点不可能同时满足条件1,2.所以p2应该删除.
标签:style blog http color sp 2014 c log r
原文地址:http://www.cnblogs.com/Acmerfighting/p/3991080.html