标签:ann log 精度 dataframe 自变量 value color orm info
本篇为《Python机器学习》一书的笔记。
一、简单线性回归模型
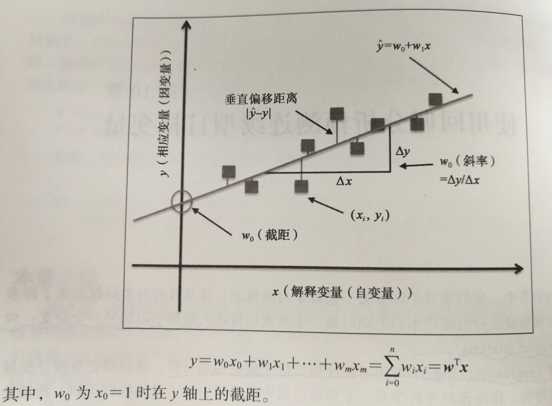
简单(单变量)线性回归的目标是:通过模型来描述某一特征(解释变量x),与连续输出(目标特征y)之间的关系。当只有一个解释变量时,线性模型的函数定义如下:
![]()
线性回归可以看成是求解样本点的最佳拟合直线,这条最佳拟合线被称为回归线,回归线与样本点之间的垂直连线即残差——预测的误差,如图所示:
python做简单线性回归模型(即只有一个解释变量x)
#导入库 import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt import seaborn as sns #Seaborn是基于matplotlib的python数据可视化库 from sklearn.linear_model import LinearRegression #获取数据 boston=datasets.load_boston() data=boston.data target=boston.target df=pd.DataFrame(data,columns=[‘CRIM‘,‘ZN‘,‘INDUS‘,‘CHAS‘,‘NOX‘,‘RM‘,‘AGE‘,‘DIS‘,‘RAD‘,‘TAX‘,‘PTRATIO‘,‘B‘,‘LSTAT‘]) df[‘MEDV‘]=pd.DataFrame(target) print(df.head()) #画散点图 pd.scatter_matrix(df,diagonal=‘kde‘,color=‘k‘,alpha=0.3) plt.show()
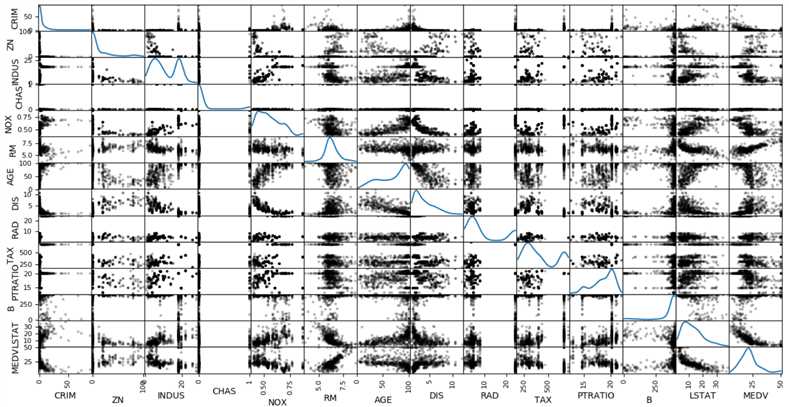
通过散点图可以了解数据的分布情况,以及是否包含异常值。从图中可看出RM与MEDV之间存在线性关系。
之后,通过创建相关系数矩阵,来量化特征之间的关系。相关系数矩阵是一个包含皮尔逊积矩相关系数的方阵,用来衡量两两特征间的线性依赖关系。取值范围-1~1。如r=1表示两个特征完全相关,r=0表示不相关,r=-1表示两个特征完全负相关。

#构造相关系数矩阵 cm=np.corrcoef(df.values.T) sns.set(font_scale=1.5) #横纵坐标字体缩放倍数 hm=sns.heatmap(cm,cbar=True,annot=True,square=True,fmt=‘.2f‘,annot_kws={‘size‘:10},yticklabels=df.columns,xticklabels=df.columns) plt.show()
参数:(引用https://zhuanlan.zhihu.com/p/28447106)
cmap:matplotlib的colormap名称或颜色对象;如果没有提供,默认为cubehelix map (数据集为连续数据集时) 或 RdBu_r (数据集为离散数据集时)
center:将数据设置为图例中的均值数据,即图例中心的数据值;通过设置center值,可以调整生成的图像颜色的整体深浅;设置center数据时,如果有数据溢出,则手动设置的vmax、vmin会自动改变。
xticklabels: 如果是True,则绘制dataframe的列名。如果是False,则不绘制列名。如果是列表,则绘制列表中的内容作为xticklabels。 如果是整数n,则绘制列名,但每个n绘制一个label。 默认为True。
yticklabels: 如果是True,则绘制dataframe的行名。如果是False,则不绘制行名。如果是列表,则绘制列表中的内容作为yticklabels。 如果是整数n,则绘制列名,但每个n绘制一个label。 默认为True。默认为True。
annot:annot默认为False,当annot为True时,在heatmap中每个方格写入数据
annot_kws:当annot为True时,可设置各个参数,包括大小,颜色,加粗,斜体字等
fmt:格式设置
cbar:是否绘制彩条,默认绘制
squar:布尔值,true则每个格斗是正方形
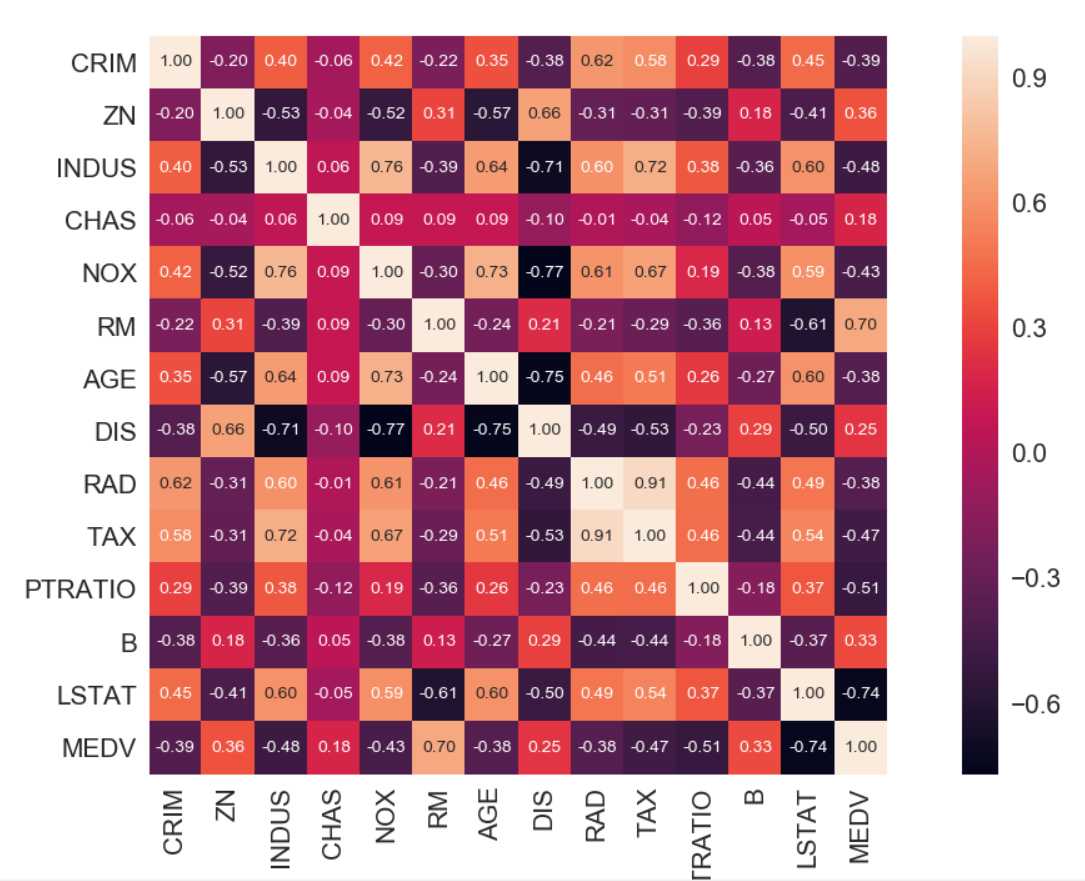
上图看出,RM和LSTAT与MEDV的相关性较大,但从散点图看出,LSTAT与MEDV之间非线性关系。所以使用RM做为解释变量进行简单线性回归模型训练。
#构造回归模型 x=df[[‘RM‘]].values y=df[‘MEDV‘].values slr=LinearRegression() slr.fit(x,y) print(‘slope:%.3f‘%slr.coef_ ) #输出x系数 print(‘intercept:%.3f‘%slr.intercept_) #输出截距
slope:9.102
intercept:-34.671
#拟合图像 plt.scatter(x,y,c=‘blue‘) plt.plot(x,slr.predict(x),c=‘red‘) plt.xlabel(‘RM‘) plt.ylabel(‘MEDV‘) plt.show()
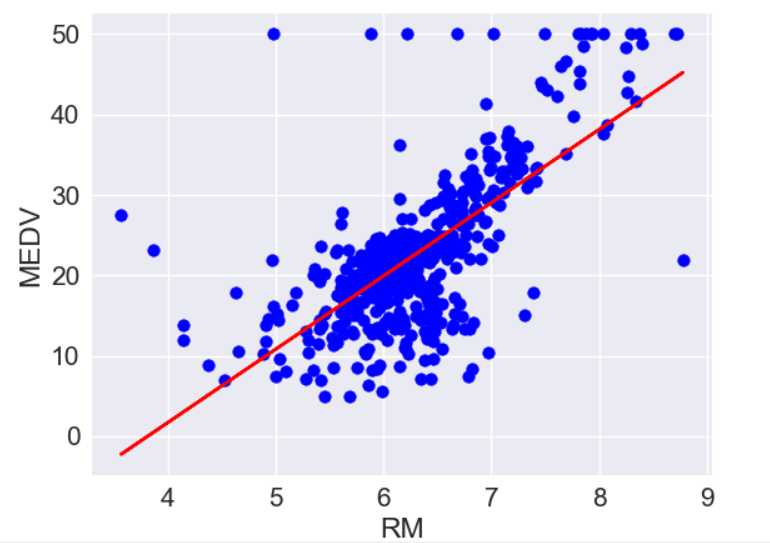
二、线性回归模型性能的评估
1.绘制残差图
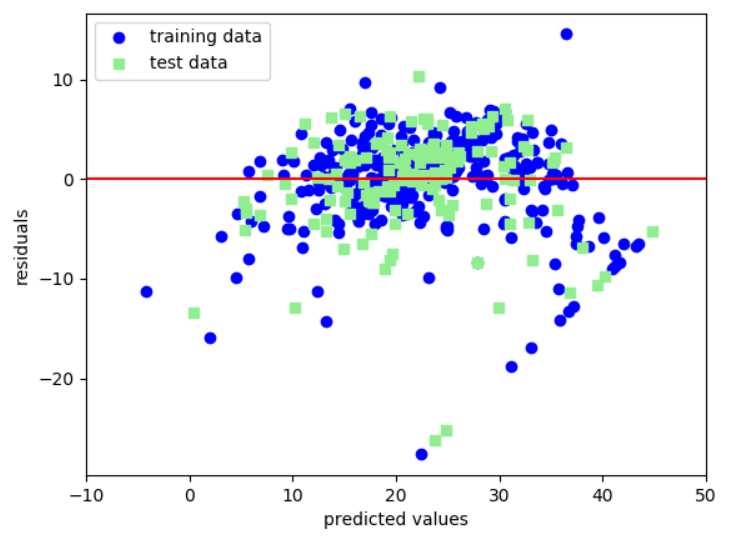
残差图可对回归模型进行评估、获取模型的异常值,同时还可检查模型是否是线性的,以及误差是否随机分布。完美的预测结果其残差为0,实际中,这种情况不会发生,故对于一个好的回归模型,我们期望误差是随机分布的,同时残差也是随机分布于中心线附近。
#多元回归模型 import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression from sklearn.cross_validation import train_test_split
#获取数据,划分训练集、测试集 boston=datasets.load_boston() x=boston.data y=boston.target x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=0)
#训练模型 slr=LinearRegression() slr.fit(x_train,y_train) y_train_pred=slr.predict(x_train) y_test_pred=slr.predict(x_test) #获取残差图 plt.scatter(y_train_pred,y_train_pred-y_train,c=‘blue‘,marker=‘o‘,label=‘training data‘) plt.scatter(y_test_pred,y_test_pred-y_test,c=‘green‘,marker=‘s‘,label=‘test data‘) plt.xlabel(‘predicted values‘) plt.ylabel(‘residuals‘) #残差 plt.legend(loc=‘best‘) plt.hlines(y=0,color=‘red‘,xmin=-10,xmax=50) plt.xlim([-10,50]) plt.show()
2、均方误差(MSE)
另一种对模型性能进行定量评估的方法是均方误差(MSE),它是线性回归模型拟合过程中,最小化误差平方和(SSE)代价函数的平均值。MSE可用于不同回归模型的比较,或是通过网格搜索进行参数调优,以及交叉验证等。
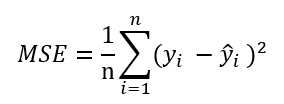
from sklearn.metrics import mean_squared_error print(‘MSE train: %.3f,test:%.3f‘%(mean_squared_error(y_train,y_train_pred),mean_squared_error(y_test,y_test_pred)))
MSE train: 19.966,test:27.18
训练集MSE值为19.96,测试集MSE骤升为27.18,说明模型过于拟合训练数据了。
3、决定系数R2
决定系数R2可以看做是MSE的标准化版本,用于更好的解释模型的性能。R2是模型捕获的响应方差的分数。
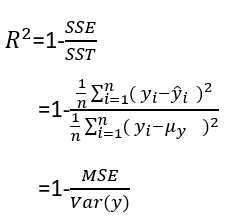
R2取值范围 [0,1] .
from sklearn.metrics import r2_score print(‘R^2 train: %.3f, test: %.3f‘%(r2_score(y_train,y_train_pred),r2_score(y_test,y_test_pred)))
R^2 train: 0.764, test: 0.674
三、岭回归、LASSO回归
岭回归:是一种专用于样本量少、存在共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
岭回归通过引入一个惩罚变量解决了普通最小二乘法的问题。
# make_regression生成回归模型数据。几个关键参数有n_samples(生成样本数), n_features(样本特征数),noise(样本随机噪音)和coef(是否返回回归系数)。
from sklearn.datasets import make_regression reg_data, reg_target = make_regression(n_samples=100, n_features=2, effective_rank=1, noise=10)
#用交叉验证的方法寻找合适的惩罚变量 from sklearn.linear_model import RidgeCV ridge=RidgeCV(alphas=[0.01,0.05,0.1,0.5,1.0,10.0]) ridge.fit(reg_data, reg_target)
#6个alpha值,对应6个误差值,最小的均值误差对应最优的alpha值
print(ridge.alpha_)
0.01
LASSO回归:LASSO回归也是对回归系数做出限定,寻找对因变量最具解释力的自变量集合,就是通过自变量选择来提供模型的解释性和预测精度。与岭回归类似,它也是通过增加惩罚函数来判断、消除特征间的共线性。
#用交叉验证的方法寻找合适的惩罚变量
from sklearn.linear_model import LassoCV lasso=LassoCV(alphas=[0.01,0.05,0.1,0.5,1.0,10.0]) lasso.fit(reg_data, reg_target) print(lasso.alpha_)
岭回归、LASSO回归参考:
https://blog.csdn.net/sa14023053/article/details/51817249
https://blog.csdn.net/SA14023053/article/details/51707514
https://blog.csdn.net/SA14023053/article/details/51707597
标签:ann log 精度 dataframe 自变量 value color orm info
原文地址:https://www.cnblogs.com/niniya/p/8878480.html