标签:measure 思路 iterator 规范 ati tps argv 修改 style
1.GitHub地址:https://github.com/Fionayxy/sudoku
2.
| PSP2.1 | Personal Software Process Stages | 预计耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 60 | 60 |
| Estimate | 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发 | 1800 | 1200 |
| Analysis | 需求分析(包括学习新技术) | 360 | 300 |
| Design Spec | 生成设计文档 | 120 | 150 |
| Design Review | 设计复审(和同事审核设计文档) | 20 | 10 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 20 | 30 |
| Design | 具体设计 | 180 | 200 |
| Coding | 具体编码 | 2000 | 360 |
| Code Review | 代码复审 | 300 | 180 |
| Test | 测试(自我测试,修改代码,提交修改) | 60 | 360 |
| Report | 报告 | 150 | 150 |
| Test Report | 测试报告 | 30 | 30 |
| Size Measurement | 计算工作量 | 10 | 10 |
| Postmortem&Process Improvement Plan | 事后总结,并提出过程改进计划 | 60 | 120 |
| 合计 | 5190 | 3180 |
3.解题思路
看到题目后毫无头绪,尤其是对命令行、GitHub等毫无了解而且对C++了解甚少,C#完全不会,因此一拖再拖。
后来在查询了main函数的参数意义,如何使用C++创建或打开本地文件、编辑文件,并在同学的帮助下,学会了github的皮毛。
(1)生成数独
刚开始百度如何生成数独,研究网上的代码和思路,进展十分缓慢。最后同学给我讲解了他的思路,即:
先定义第一行数字(学号尾号37,(3+7)%9+1=2)
int tmp[9] = { 2,3,4,5,6,7,8,9,1 };
之后8行的数字排列可看做是对第一行数字进行移动
因为九宫格中的数字不能重复,因此将2-8行右移相应格数
int moveright[8] = { 3,6,1,4,7,2,5,8 };
由于第一行第一个数应保持为2不变,对其余8个数进行全排列,一共有8!=40320种
且在每一个情况下,都可变换4-6行、7-9行的位置,即每个确定的第一行都有3!×3!=36种不同的终局
因此最终可生成终局40320×36=1451520(种)>1e6(种)
全排列时用到了 <algorithm>头文件下的函数
bool next_permutation(iterator start,iterator end)
(2)解数独
采用了递归的方法,从第一个格子开始
对每个格子,如果该格已有有效数(1-9),则遍历下一格,若没有有效数,则从1-9寻找满足条件(行、列、九宫格无重复数字)的所有侯选数
遍历直至最后一个格子,输出当前数独
由于本题只要求输出一个可行解,因此在首次输出后,直接结束即可。
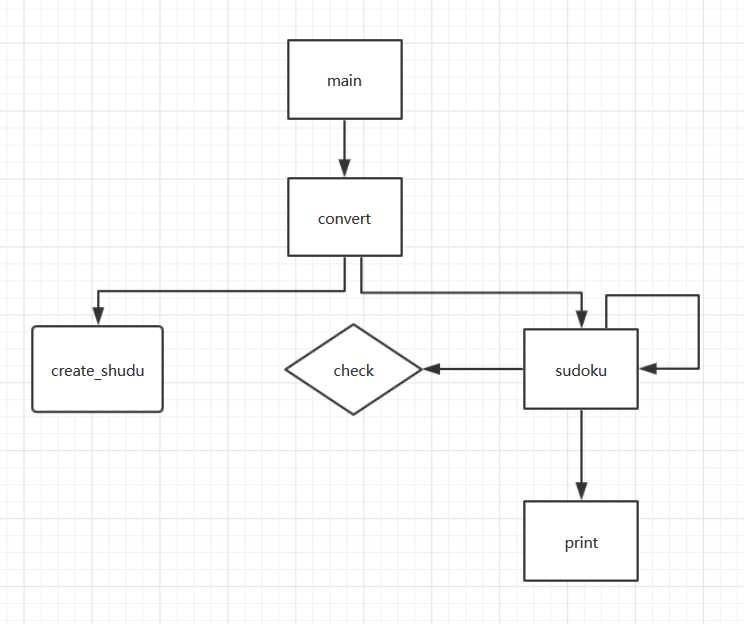
4.设计实现过程
int main(int argc, char *argv[]) void Sudoku(int a[9][9], int n) //数独求解函数 bool check(int a[9][9], int i, int j, int k)//判断是否可以将第i行、第j列的数设为k void print(int a[9][9])//输出可行的解 int convert(char* str)//判断输入的字符串是否均为数字(即n) void creat_shudu() //生成终局并输出到sudoku文件中
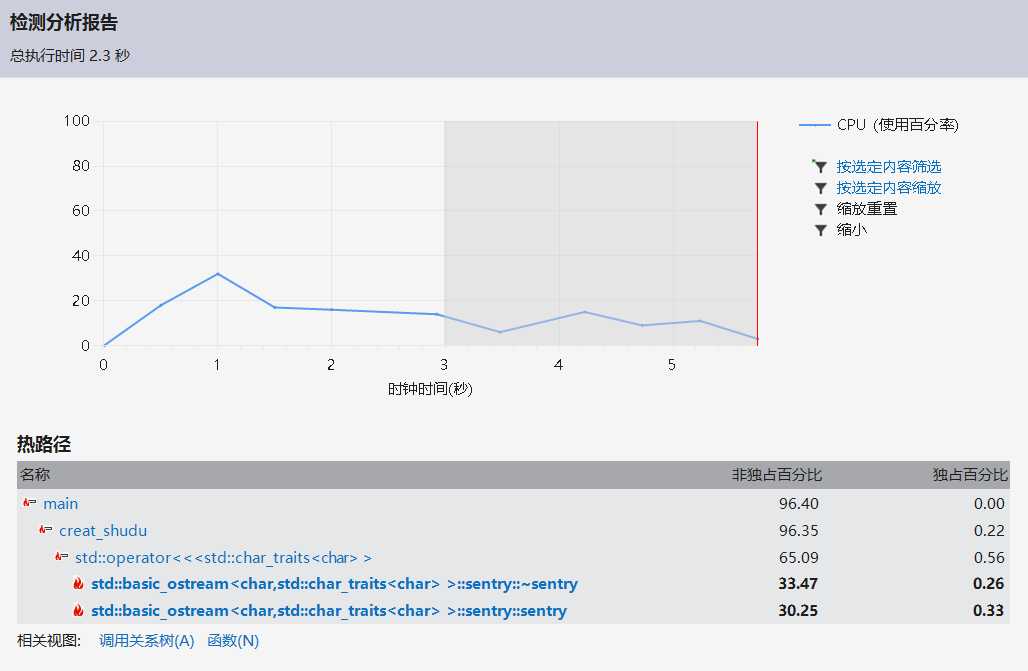
5.性能分析
生成500个数独终局
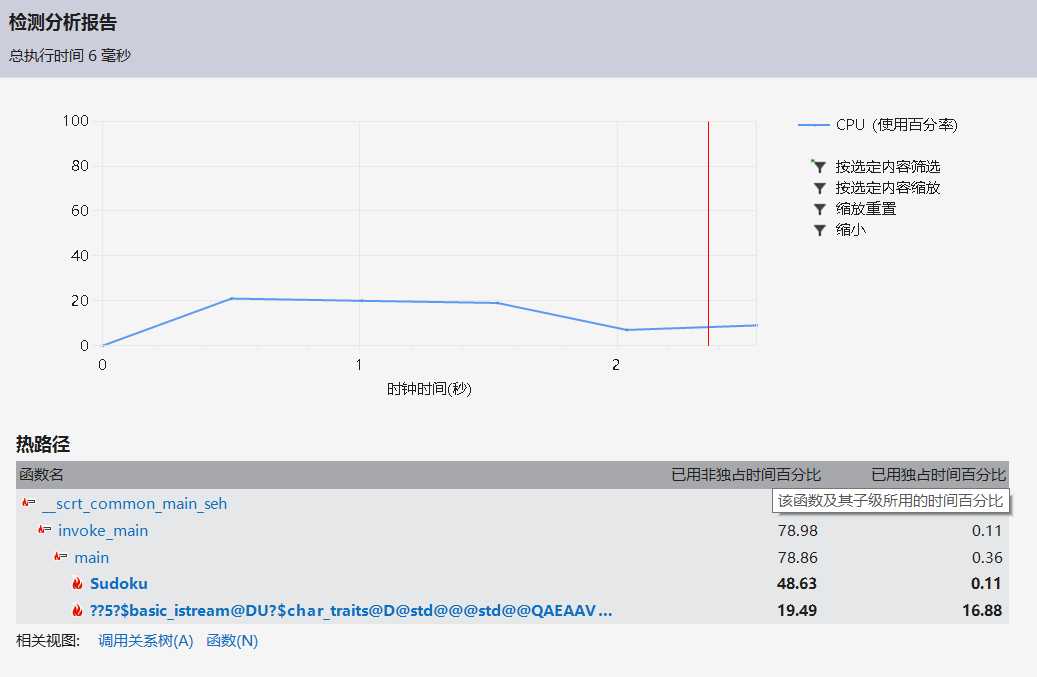
解数独测试用例
0 8 0 0 0 1 6 0 0
0 7 0 4 0 0 0 2 1
5 0 0 3 9 6 0 0 0
2 0 4 0 5 0 1 3 0
0 0 8 9 0 7 5 0 0
0 5 7 0 3 0 9 0 0
0 0 0 5 6 3 0 0 9
3 1 0 0 0 2 0 5 0
0 0 5 8 0 0 0 4 0
0 1 2 6 8 0 0 9 0
6 0 0 0 0 4 0 1 0
8 0 5 2 0 0 3 7 0
0 0 0 0 0 7 5 2 3
0 0 0 4 0 6 0 0 0
3 8 1 9 0 0 0 0 0
0 5 4 0 0 2 8 0 1
0 7 0 3 0 0 0 0 2
0 3 0 0 5 9 7 6 0
0 4 7 0 5 0 0 0 8
6 0 5 0 3 0 2 0 1
0 0 0 7 0 6 0 3 0
0 0 6 0 7 0 0 2 4
9 0 0 8 0 4 0 0 6
4 5 0 0 1 0 9 0 0
0 1 0 5 0 2 0 0 0
2 0 8 0 4 0 5 0 3
5 0 0 0 9 0 7 1 0
0 0 9 0 0 1 6 2 0
5 7 0 0 2 8 0 3 0
3 0 0 7 0 0 0 0 4
8 9 0 0 7 0 4 0 0
0 6 0 5 0 3 0 9 0
0 0 1 0 9 0 0 7 6
6 0 0 0 0 7 0 0 8
0 4 0 1 3 0 0 6 5
0 2 7 6 0 0 9 0 0
6.代码说明
(1)解数独
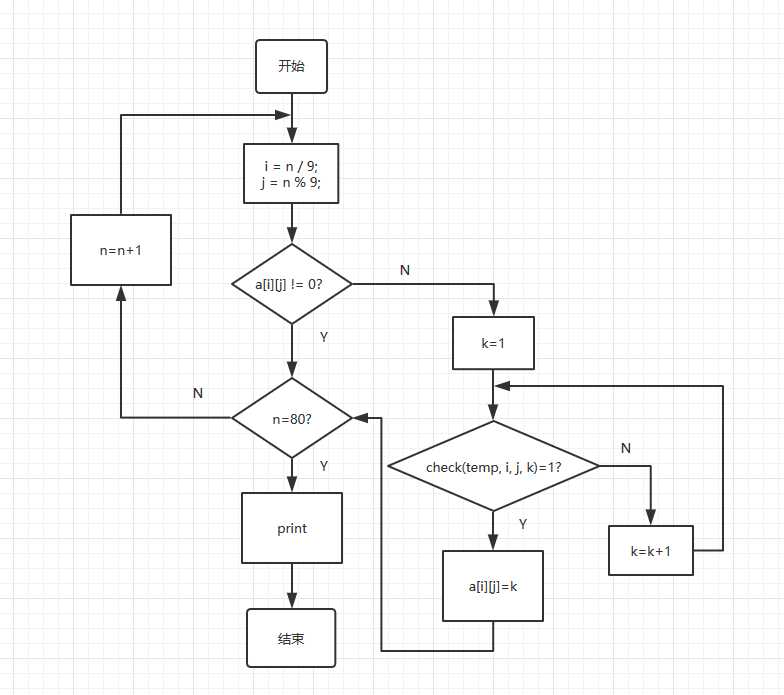
void Sudoku(int a[9][9], int n) { int temp[9][9]; int i, j; for (i = 0; i<9; i++) { for (j = 0; j<9; j++) temp[i][j] = a[i][j]; } i = n / 9; j = n % 9; //求出第n个数的行数和列数 if (a[i][j] != 0) { //已经有原始数据 if (n == 80) { //是最后一个格子,输出可行解 print(temp); } else //不是最后一个格子,求下一个格子 Sudoku(temp, n + 1); } else { //没有数据 for (int k = 1; k <= 9; k++) { bool flag = check(temp, i, j, k); if (flag) { //第i行、第j列可以是k temp[i][j] = k; //设为k if (n == 80) { print(temp); break; } else Sudoku(temp, n + 1); temp[i][j] = 0; //恢复为0,判断下一个k } } } }
(2)生成终局
void creat_shudu() //生成终局并输出到sudoku文件中 { int tmp[9] = { 2,3,4,5,6,7,8,9,1 };//tmp表示第一行数字 int i, j, k, moveright[8] = { 3,6,1,4,7,2,5,8 }; //右移位数 for (i = 0; i < 40320; i++) //8!=40320 { memcpy(map[0], tmp, sizeof(tmp)); for (j = 0; j < 8; j++) for (k = 0; k < 9; k++) map[j + 1][(k + moveright[j]) % 9] = map[0][k];//初始模板 int row[9] = { 0,1,2,3,4,5,6,7,8 };//fol函数是接下来输出的1-9行对应数独模板的fol行 for (j = 0; j < 6; j++) { if (j != 0) next_permutation(row + 3, row + 6);//此函数是求4-7行的下一个排列 for (k = 0; k < 6; k++) { if (k != 0) next_permutation(row + 6, row + 9); for (int a = 0; a < 9; a++) { for (int b = 0; b < 9; b++) { if (b == 0) output << map[row[a]][b]; else output << " " << map[row[a]][b]; } output << endl; } output << endl; if (!--n) return; }//完成一次数独的输出 row[6] = 7, row[7] = 8, row[8] = 9; }//每种数独模板有36种形式,最多能输出8!*36=1451520种 next_permutation(tmp + 1, tmp + 9);//对tmp函数进行一次全排列 } return; }
标签:measure 思路 iterator 规范 ati tps argv 修改 style
原文地址:https://www.cnblogs.com/y-x-y/p/8886415.html