标签:sea pad uniq search 大于 begin 序列 最大连续子数组和 最小
1、最长递增子序列
upper_bound(ends.begin(),ends.end(),num) > 返回指向范围[first, last) 中首个大于value 的元素的迭代器
ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value ); >= 返回指向范围[first, last) 中首个不小于(即大于或等于)value 的元素的迭代器
1 2 class Solution { 3 public: 4 int lengthOfLIS(vector<int>& nums) { 5 if (nums.empty()) return 0; 6 vector<int> res; // 定义 7 res.push_back(nums[0]); 8 int len = 0; 9 for (int i = 1; i < nums.size(); i++) { 10 int pos = binarySearch(res, nums[i]); 11 if (pos == res.size()) { 12 res.push_back(nums[i]); 13 } 14 else res[pos] = nums[i]; 15 } 16 return res.size(); 17 18 19 } 20 21 int binarySearch(vector<int>& res, int num) { 22 int low = 0, high = res.size() - 1; 23 while (low + 1 < high) { 24 int mid = low + (high - low) / 2; 最好不要用移位,容易出错 25 // 找到>=num的第一个数的位置 26 if (res[mid] == num) { 27 return mid; 28 } else if (res[mid] < num){ 29 low = mid; 30 } else { 31 high = mid; 32 } 33 } 34 35 if (res[high] < num) { 36 return res.size(); 37 } else if (res[low] >= num) { 38 return low; 39 } else { 40 return high; 41 } 42 } 43 // int lengthOfLIS(vector<int>& nums) { 44 //O(n^2) 45 // int res = 0; // 不初始化,编译器默认初始化为极大值 46 // vector<int> dp(nums.size(), 1); 47 // for (int i = 0; i < nums.size(); i++) { 48 // for (int j = 0; j <= i; j++) { 49 // if (nums[j] < nums[i]) { 50 // dp[i] = max(dp[i], dp[j]+1); 51 // } 52 // } 53 // res = max(res, dp[i]); 54 // } 55 // return res; 56 57 58 //O(nlogn) Binary search normal or STL O(nlogn) 59 // https://leetcode.com/problems/longest-increasing-subsequence/discuss/74897/Fast-Java-Binary-Search-Solution-with-detailed-explanation 60 // if (nums.empty()) return 0; 61 // vector<int> res; 62 // for (int i = 0; i < nums.size(); i++) { 63 // // int pos = binarySearch(res, nums[i]); 64 // auto it = lower_bound(res.begin(), res.end(), nums[i]); 65 // if (it == res.end()) { 66 // res.push_back(nums[i]); 67 // } else { 68 // *it = nums[i]; 69 // } 70 // } 71 // return res.size(); 72 73 // } 74 75 76 }; 77
2、寻找最小的k 个数
set和multiset会根据特定的排序准则,自动将元素进行排序。不同的是后者允许元素重复而前者不允许。
sort(a ,a + len, greater<int>());//内置类型的由大到小排序
sort(a ,a + len, greater<int>());//内置类型的由大到小排序
方法一:适用于海量数据 堆排序原理 维护一个最大k堆 O(nlogk) 堆排序写法 1. /* 2. arr[start+1...end]满足小顶堆的定义, 3. 将arr[start]加入到小顶堆arr[start+1...end]中, 4. 调整arr[start]的位置,使arr[start...end]也成为小顶堆 5. 注:由于数组从0开始计算序号,也就是二叉堆的根节点序号为0, 6. 因此序号为i的左右子节点的序号分别为2i+1和2i+2 7. */ 8. void HeapAdjustDown(int *arr,int start,int end) 9. { 10. int temp = arr[start]; //保存当前节点 11. int i = 2*start+1; //该节点的左孩子在数组中的位置序号 12. while(i<=end) 13. { 14. //找出左右孩子中最小的那个 15. if(i+1<=end && arr[i+1]<arr[i]) 16. i++; 17. //如果符合堆的定义,则不用调整位置 18. if(arr[i]>=temp) 19. break; 20. //最小的子节点向上移动,替换掉其父节点 21. arr[start] = arr[i]; 22. start = i; 23. i = 2*start+1; 24. } 25. arr[start] = temp; 26. } 27. 28. /* 29. 得到最小的k个数,保存在arr中的最后面k个位置 30. */ 31. void MinHeapKNum(int *arr,int len,int k) 32. { 33. if(arr==NULL || len<1 || k<1 || k>len) 34. return; 35. 36. int i; 37. //把数组建成为小顶堆 38. //第一个非叶子节点的位置序号为(len-1)/2 39. for(i=(len-1)/2;i>=0;i--) 40. HeapAdjustDown(arr,i,len-1); 41. //进行堆排序 42. for(i=len-1;i>=len-k;i--) 43. { 44. //堆顶元素和最后一个元素交换位置, 45. //这样最后的一个位置保存的是最小的数, 46. //每次循环依次将次小的数值在放进其前面一个位置, 47. int temp = arr[i]; 48. arr[i] = arr[0]; 49. arr[0] = temp; 50. //将arr[0...i-1]重新调整为小顶堆 51. HeapAdjustDown(arr,0,i-1); 52. } 53. }
方法二:partition方法 O(n) 明日待续
3、寻找和为定值的两个数 2sum考虑map,find只能找到迭代器。注意unique条件怎么处理 数组如果事先排序会怎样。
empty()比size()好,时间复杂度常规值,size()==0随容器不同改变
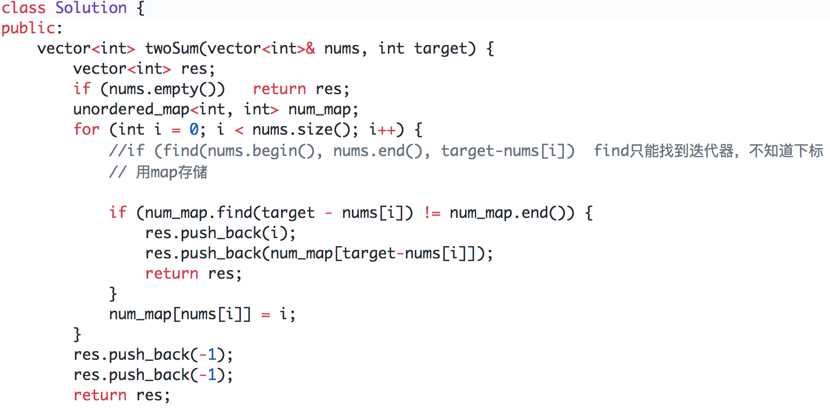
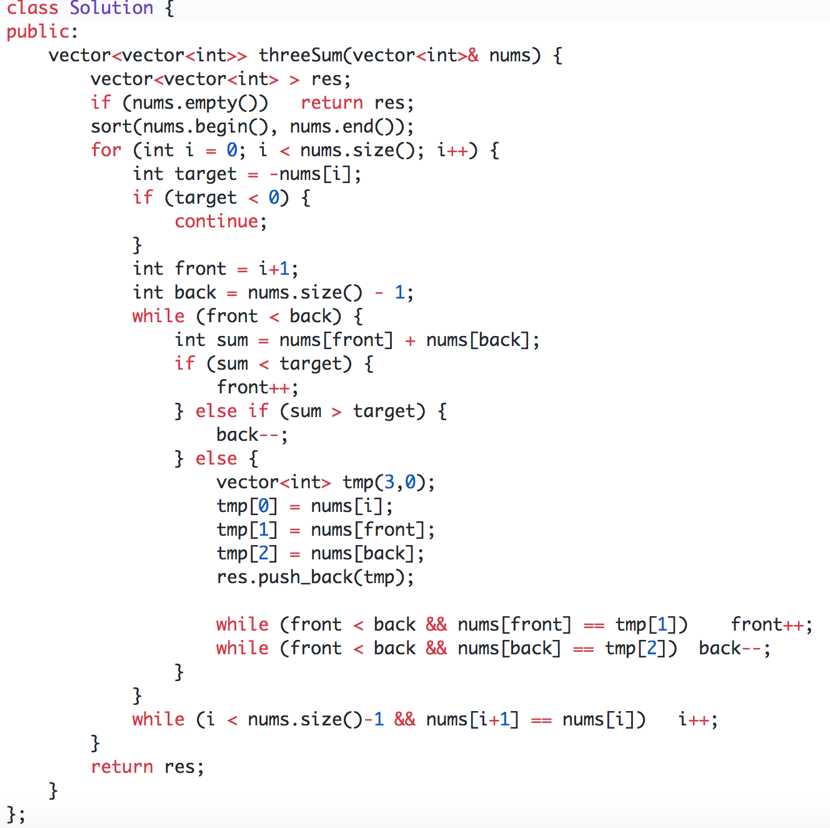
3sum unique 和为0的所有组合
4、最大连续子数组和 列出动规公式,从后往前推 记录最大值
数组最好初始化大小:vector<int> dp(nums.size()); 否则容易内存free错误(同一块内存两次free,内存溢出,使用不应访问的内存等)

5、跳台阶 可跳1台阶 2台阶 ... n台阶

标签:sea pad uniq search 大于 begin 序列 最大连续子数组和 最小
原文地址:https://www.cnblogs.com/li-ling/p/8904133.html