HDU 6201【最长路+SPFA转化为流问题求解***】

标签：empty   push   value   head   sizeof   while   转化   size   info   

题意: 给出一棵生成树，每个点有一个权值，代表商品的售价，树上每一条边上也有一个权值，代表从这条边经过所需要的花费。现在需要你在树上选择两个点，一个作为买入商品的点，一个作为卖出商品的点，当然需要考虑从买入点到卖出点经过边的花费。使得收益最大。允许买入点和卖出点重合，即收益最小值为0.

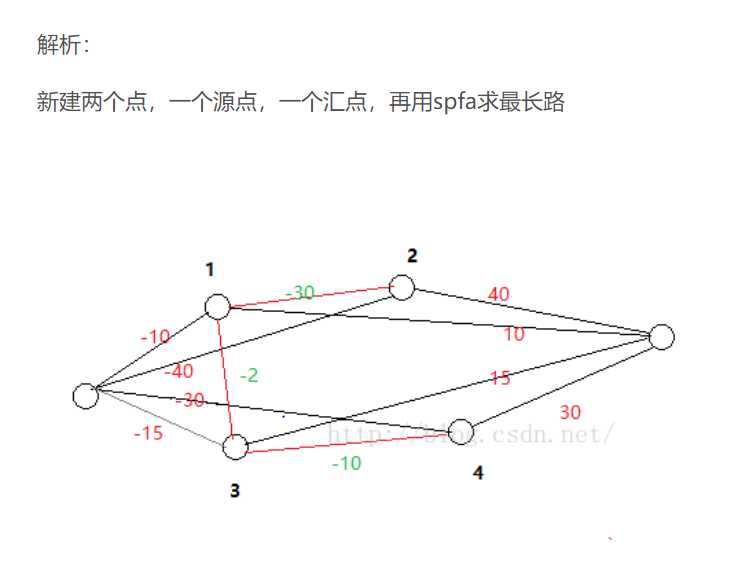
这个题不用树形DP也能求，实在是太巧妙。贴一个别人的解法

#include<cstdio>  
#include<cstring>  
#include<algorithm>  
#include<vector>  
#include<queue>  
using namespace std;

const int MAXN = 500010;
const int INF = 2000;

typedef struct node {
    int from;
    int to;
    int value;
    int next;
}node;

node edge[MAXN];
int head[MAXN], cnt, n;
int d[MAXN], vis[MAXN];
void addedge(int from, int to, int value) {
    edge[cnt].from = from;
    edge[cnt].to = to;
    edge[cnt].value = value;
    edge[cnt].next = head[from];
    head[from] = cnt++;
}

void spfa(int s, int e) {
    queue<int> mq;
    mq.push(s);
    vis[s] = 1;
    d[s] = 0;
    while (!mq.empty()) {
        int front = mq.front();
        mq.pop();
        vis[front] = 0;
        for (int i = head[front]; i != -1; i = edge[i].next) {
            int to = edge[i].to;
            int value = edge[i].value;

            if (d[to] < d[front] + value) {
                d[to] = d[front] + value;
                if (!vis[to]) {
                    mq.push(to);
                    vis[to] = 1;

                }

            }

        }

    }

}

int main(void) {
    int t;
    scanf("%d", &t);
    while (t--) {
        memset(head, -1, sizeof(head));
        cnt = 0;
        scanf("%d", &n);
        int a, b, c;
        for (int i = 1; i <= n; i++) {
            scanf("%d", &b);
            addedge(0, i, -b);
            addedge(i, n + 1, b);
        }
        for (int i = 1; i <= n - 1; i++) {
            scanf("%d%d%d", &a, &b, &c);
            addedge(a, b, -c);
            addedge(b, a, -c);
        }
        memset(vis, 0, sizeof(vis));
        for (int i = 0; i <= n + 1; i++)
            d[i] = -INF;

        spfa(0, n + 1);
        printf("%d\n", d[n + 1]);
    }

    return 0;
}

HDU 6201【最长路+SPFA转化为流问题求解***】

标签：empty   push   value   head   sizeof   while   转化   size   info   

原文地址：https://www.cnblogs.com/tennant/p/8906093.html