标签:unsigned wol cstring inline 需要 div getc || 地方
Description
成都的驾驶考试在一个有n条平行的自南向北的单向的道路的场地中进行。每条道路长度为m米,并且都在同一条水平线上开始和结束。街道从西向东分别编号为1到n。同样有p条单向的自西向东或自东向西的街道垂直于上面描述的街道,每一条这样的街道链接了两个相邻的自南向北的道路。当然自西向东和自东向西的道路可以重叠,那就是一个双向的街道了。
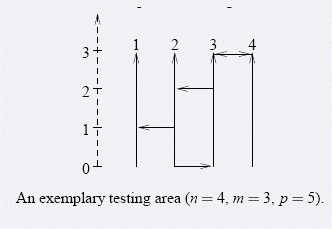
考生选择一个自南向北的道路作为他考试的起始点和另外一个自南向北的道路作为他考试的终止点。他们的考试项目是将车从开始的道路驾驶到作为终止点的道路。考生们总是选择一个可以到达所有其他街道的起始道路作为开始点。现在,考生们总是感到十分无趣因为他们只有很少的起始道路可以选择,所以教练们决定改造先有的考试场所,由于经费的限制,他们决定添加至多K条东西向的道路,使得能够选择的起始道路尽量地多。
Input
输入第一行包含四个整数n,m,p和k(2<=n<=100000, 1<=m,k<=100000, 0<=p<=100000)。分别表示南北向的道路数,南北向道路的长度,东西向的道路数和最多能够添加的道路数。接下来p行,每行包含三个整数ni,mi和di(1 < = ni < n,0 < = mi < m,di = 0 or 1),表示一条自西向东(di = 0)或者自东向西(di = 1)的道路。这个道路连接了南北向的道路ni和ni+1,在第mi米的地方进行了连接。
Output
输出中仅包含一个整数,最大的能够作为起点的道路数(不包括原来就能作为起点的道路数)。注意添加的道路不能与南北向的道路相交,并且到起始水平线的距离为整数。添加的道路可以重叠,表示双向的道路。
Sample Input
4 3 5 2
2 0 0
2 2 1
3 3 1
1 1 1
3 3 0
Sample Output
2
HINT
首先跪%一波大神的题解
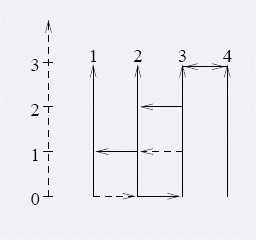
我们考虑一下这道题,i可以作为起点,那么i就可以到第1条和第n条南北道路,如果我们将边反过来,就说明如果第1和第n条路可以到达i,那么i就是一个合法的起点。
我们设fl[i]表示从1到达i需要添加的边数,设fr[i]表示从i到达n需要添加的边数,然后我们可以发现,fl[i]=i-1-左边的最长不降子序列长度,这个可以用树状数组\(O(n log n)\)维护,fr[i]亦然
最后我们要求i,j(i<=j),使得fr[i]+fl[j]<=k
由于fl单调递增,fr单调递减,双指针维护一下即可
/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<‘0‘||ch>‘9‘;ch=getchar()) if (ch==‘-‘) f=-1;
for (;ch>=‘0‘&&ch<=‘9‘;ch=getchar()) x=(x<<1)+(x<<3)+ch-‘0‘;
return x*f;
}
inline void print(int x){
if (x>=10) print(x/10);
putchar(x%10+‘0‘);
}
const int N=1e5;
int tree[N+10],f[N+10];
int fl[N+10],fr[N+10];
int n,m,p,k;
struct S1{
int pre[N+10],now[N+10],child[N+10],tot;
void join(int x,int y){pre[++tot]=now[x],now[x]=tot,child[tot]=y;}
}L,R;
void insert(int x,int v){for (;x<=m;x+=lowbit(x)) tree[x]=max(tree[x],v);}
int query(int x){
int res=0;
for (;x;x-=lowbit(x)) res=max(res,tree[x]);
return res;
}
int main(){
n=read(),m=read()+1,p=read(),k=read();
int Ans=0,cnt=0;
for (int i=1;i<=p;i++){
int x=read(),y=m-read(),t=read();
t?L.join(x+1,y):R.join(x,y);
}
for (int i=1,res=0;i<=n;i++){
for (int p=L.now[i],son=L.child[p];p;p=L.pre[p],son=L.child[p]) res=max(res,f[p]=query(son)+1);
for (int p=L.now[i],son=L.child[p];p;p=L.pre[p],son=L.child[p]) insert(son,f[p]);
fl[i]=i-1-res;
}
memset(f,0,sizeof(f));
memset(tree,0,sizeof(tree));
for (int i=n,res=0;i;i--){
for (int p=R.now[i],son=R.child[p];p;p=R.pre[p],son=R.child[p]) res=max(res,f[p]=query(son)+1);
for (int p=R.now[i],son=R.child[p];p;p=R.pre[p],son=R.child[p]) insert(son,f[p]);
fr[i]=n-i-res;
}
for (int i=1,j=1;i<=n;i++){
while (j<=n&&fr[i]+fl[j]<=k) j++;
Ans=max(Ans,j-i);
if (!fl[i]&&!fr[i]) cnt++;
}
printf("%d\n",Ans-cnt);
return 0;
}标签:unsigned wol cstring inline 需要 div getc || 地方
原文地址:https://www.cnblogs.com/Wolfycz/p/8905747.html