标签:需要 com 问题 nbsp 关系 函数 情况 技术 inf
如果我们把二叉树看成一个图,父子节点之间的连线看成是双向的,我们姑且定义 " 距离 " 为两节点之间边的个数。写一个程序,求一棵二叉树中相距最远的两个节点之间的距离,求二叉树中节点的最大距离
分析: 先画几个不同形状的二叉树,从例子中可以看出,相距最远的两个节点,一定是两个叶子节点,或者是一个叶子节点到它的根节点:
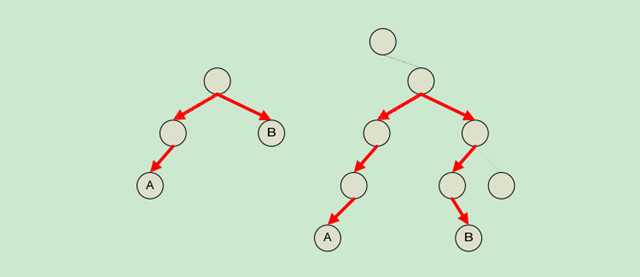
根据相距最远的两个节点一定是叶子节点这个规律,我们可以进一步讨论。 对于任意一个节点,以该节点为根,假设这个根有 K 个孩子节点,那么相距最远的两 个节点 U和 V之间的路径与这个根节点的关系有两种情况:
1. 若路径经过根Root,则U和V是属于不同子树的,且它们都是该子树中到根节点最远的节点,否则跟它们的距离最远相矛盾。
2. 如果路径不经过Root,那么它们一定属于根的K个子树之一。并且它们也是该子树中相距最远的两个顶点。
所以,只需要计算这两种情况的路径距离,并取其大者,就是该二叉树的最大距离。
递归:
1. 先弄清楚递归的顺序。在递归的实现中,往往需要假设后续的调用已经完成,在此基础之上,才实现递归的逻辑。在该题中,我们就是假设已经把后面的长度计算出来了,然后继续考虑后面的逻辑;
2. 分析清楚递归体的逻辑,然后写出来。比如在上面的问题中,递归体的逻辑就是如何计算两边最长的距离;
3.
考虑清楚递归退出的边界条件。也就说,哪些地方应该写return。
注意到以上 3 点,在面对递归问题的时候,我们将总是有章可循。
经过以上的分析,我们可以看出,情况1及2需要不同的信息: 情况1需要子树的最大深度,情况2需要子树的最大距离。只要函数能在一个节点同时计算及传回这两个信息,代码就可以很简单:
int maxDistance(Node * root)
{
int depth;
return helper(root, depth);
}
int helper(Node * root, int &depth)
{
if (root == NULL)
{
depth = 0;
return 0;
}
int ld, rd;
int maxleft = helper(root->left, ld);
int maxright = helper(root->right, rd);
depth = max(ld, rd)+1;
return max(maxleft, max(maxright, ld+rd));
}
标签:需要 com 问题 nbsp 关系 函数 情况 技术 inf
原文地址:https://www.cnblogs.com/always-fight/p/8919734.html