标签:temp dfs load ons get main 输出 const 答案
lrb有一棵树,树的每个节点有个颜色。给一个长度为n的颜色序列,定义s(i,j) 为i 到j 的颜色数量。以及
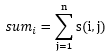
现在他想让你求出所有的sum[i]
输入格式:
第一行为一个整数n,表示树节点的数量
第二行为n个整数,分别表示n个节点的颜色c[1],c[2]……c[n]
接下来n-1行,每行为两个整数x,y,表示x和y之间有一条边
输出格式:
输出n行,第i行为sum[i]
输入样例#1:
5
1 2 3 2 3
1 2
2 3
2 4
1 5
输出样例#1:
10
9
11
9
12
sum[1]=s(1,1)+s(1,2)+s(1,3)+s(1,4)+s(1,5)=1+2+3+2+2=10
sum[2]=s(2,1)+s(2,2)+s(2,3)+s(2,4)+s(2,5)=2+1+2+1+3=9
sum[3]=s(3,1)+s(3,2)+s(3,3)+s(3,4)+s(3,5)=3+2+1+2+3=11
sum[4]=s(4,1)+s(4,2)+s(4,3)+s(4,4)+s(4,5)=2+1+2+1+3=9
sum[5]=s(5,1)+s(5,2)+s(5,3)+s(5,4)+s(5,5)=2+3+3+3+1=12对于40%的数据,n<=2000
对于100%的数据,1<=n,c[i]<=10^5
用的点分治做
这道题我看题解都看了很久啊
nyg和zlt用虚树做的,于是我就只能默默地一个人看点分的做法
首先看找到分治中心后看怎么算根的答案,因为点对中一个点一定是根,所以就是求每个点到根的路径上有多少个不同的颜色;然后把计算答案的方法变一下,把统计点的贡献变成统计颜色的贡献
那么如果一个点的颜色是在这个点到根的路径上第一次出现,那么这个颜色就可以对答案贡献当前点的size大小贡献(因为点对中另一个点只要是这个点的子树中的点,那么由于会经过当前点,而这个点的颜色又是第一次出现,那么肯定每个点对的贡献都会加1,那么对于这个颜色来说,就会加size贡献)
\(colvl[x]\) 代表颜色 \(x\) 的贡献,\(allval\) 就是统计 \(colvl\) 的和
那么根的答案就直接为 \(allval\)
由于分治算的答案都是必经过根的,所以我们接着会发现开始我们统计的 \(colvl[i]\) 同样使用于除根外的其它点 \(x\) ,但要保证 \(x\) 到根的路径上不能出现 \(i\) 的颜色,并且同一子树中的点不能对其颜色有贡献,这不就是点分不去重的搞法吗
然后就好了
每次找完root后,dfs一遍算 \(colvl\) 和 \(allval\),然后把根的贡献搞出来
然后枚举每一个子树,dfs一遍把当前的子树的贡献去掉,再dfs一遍把去掉贡献的子树的答案算一下,最后dfs一遍把去掉的贡献加回来
点分治就做完了
#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=100000+10,inf=0x3f3f3f3f;
int n,col[MAXN],e,to[MAXN<<1],nex[MAXN<<1],beg[MAXN],Msonsize[MAXN],size[MAXN],root,colnt[MAXN],finish[MAXN];
ll allval,colvl[MAXN],ans[MAXN];
template<typename T> inline void read(T &x)
{
T data=0,w=1;
char ch=0;
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void insert(int x,int y)
{
to[++e]=y;
nex[e]=beg[x];
beg[x]=e;
}
inline void getroot(int x,int f,int total)
{
Msonsize[x]=0;size[x]=1;
for(register int i=beg[x];i;i=nex[i])
if(to[i]==f||finish[to[i]])continue;
else
{
getroot(to[i],x,total);
size[x]+=size[to[i]];
chkmax(Msonsize[x],size[to[i]]);
}
chkmax(Msonsize[x],total-size[x]);
if(Msonsize[x]<Msonsize[root])root=x;
}
inline void dfs1(int x,int f)
{
colnt[col[x]]++;
size[x]=1;
for(register int i=beg[x];i;i=nex[i])
if(to[i]==f||finish[to[i]])continue;
else dfs1(to[i],x),size[x]+=size[to[i]];
if(colnt[col[x]]==1)
{
allval+=size[x];
colvl[col[x]]+=size[x];
}
colnt[col[x]]--;
}
inline void dfs2(int x,int f,int k)
{
colnt[col[x]]++;
for(register int i=beg[x];i;i=nex[i])
if(to[i]==f||finish[to[i]])continue;
else dfs2(to[i],x,k);
if(colnt[col[x]]==1)
{
allval+=k*size[x];
colvl[col[x]]+=k*size[x];
}
colnt[col[x]]--;
}
inline void dfs3(int x,int f,int other,int colnm)
{
colnt[col[x]]++;
if(colnt[col[x]]==1)allval-=colvl[col[x]],colnm++;
ans[x]+=(ll)allval+(ll)colnm*other;
for(register int i=beg[x];i;i=nex[i])
if(to[i]==f||finish[to[i]])continue;
else dfs3(to[i],x,other,colnm);
if(colnt[col[x]]==1)allval+=colvl[col[x]],colnm--;
colnt[col[x]]--;
}
inline void clear(int x,int f)
{
colnt[col[x]]=colvl[col[x]]=0;
for(register int i=beg[x];i;i=nex[i])
if(to[i]==f||finish[to[i]])continue;
else clear(to[i],x);
}
inline void calc(int x)
{
allval=0;
dfs1(x,0);
ans[x]+=allval;
for(register int i=beg[x];i;i=nex[i])
if(!finish[to[i]])
{
colnt[col[x]]++;
allval-=size[to[i]];
colvl[col[x]]-=size[to[i]];
dfs2(to[i],x,-1);
colnt[col[x]]--;
dfs3(to[i],x,size[x]-size[to[i]],0);
colnt[col[x]]++;
allval+=size[to[i]];
colvl[col[x]]+=size[to[i]];
dfs2(to[i],x,1);
colnt[col[x]]--;
}
clear(x,0);
}
inline void solve(int x)
{
calc(x);
finish[x]=1;
for(register int i=beg[x];i;i=nex[i])
if(!finish[to[i]])
{
root=0;
getroot(to[i],x,size[to[i]]);
solve(root);
}
}
int main()
{
read(n);
for(register int i=1;i<=n;++i)read(col[i]);
for(register int i=1;i<n;++i)
{
int u,v;
read(u);read(v);
insert(u,v);insert(v,u);
}
Msonsize[0]=inf;
getroot(1,0,n);
solve(root);
for(register int i=1;i<=n;++i)write(ans[i],'\n');
return 0;
}标签:temp dfs load ons get main 输出 const 答案
原文地址:https://www.cnblogs.com/hongyj/p/8932940.html