标签:tps 大写 family algorithm || 第一个 bool 要求 out
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设x1,x2,x3...代表程序中出现的变量,给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:x1=x2,x2=x3,x3=x4,x4≠x1,这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式:
从文件prog.in中读入数据。
输入文件的第1行包含1个正整数t,表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第1行包含1个正整数n,表示该问题中需要被满足的约束条件个数。接下来n行,每行包括3个整数i,j,e,描述1个相等/不等的约束条件,相邻整数之间用单个空格隔开。若e=1,则该约束条件为xi=xj;若?e=0,则该约束条件为xi≠xj;
输出格式:
输出到文件 prog.out 中。
输出文件包括t行。
输出文件的第 k行输出一个字符串“ YES” 或者“ NO”(不包含引号,字母全部大写),“ YES” 表示输入中的第k个问题判定为可以被满足,“ NO” 表示不可被满足。
【样例解释1】
在第一个问题中,约束条件为:x1=x2,x1≠x2。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为:x1=x2,x1=x2。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个:x1=x2,x2=x3,x3=x1。只需赋值使得x1=x1=x1,即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个:x1=x2,x2=x3,x3=x4,x4≠x1。由前三个约束条件可以推出x1=x2=x3=x4,然而最后一个约束条件却要求x1≠x4,因此不可被满足。
【数据范围】
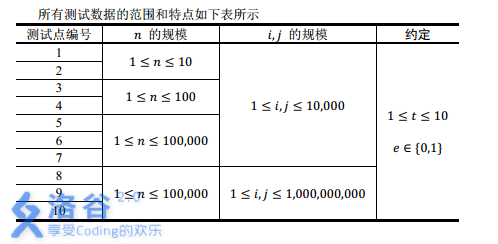
【时限2s,内存512M】
分析:一眼可知是并查集,问题就在离散化,数据范围肯定不能直接上。但是蒟蒻并不擅长离散化,一开始还好感人地打了个hash,搞了半天结果屏幕上wa声一片……然后翻了翻大佬们的博客,发现。。。模个数就行了(O.o)。。好吧,是我太蒻了。
Code:
1 //It is made by HolseLee on 24th Apr 2018 2 //Luogu.org P1955 3 #include<cstdio> 4 #include<cstring> 5 #include<cstdlib> 6 #include<cmath> 7 #include<iostream> 8 #include<iomanip> 9 #include<algorithm> 10 using namespace std; 11 const int mod=528419; 12 const int N=1e5+7; 13 int n,T,cnt,fa[mod+7],rank[mod+7]; 14 struct Ques{int x,y;}a[N]; 15 inline int read() 16 { 17 char ch=getchar();int num=0;bool flag=false; 18 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)flag=true;ch=getchar();} 19 while(ch>=‘0‘&&ch<=‘9‘){num=num*10+ch-‘0‘;ch=getchar();} 20 return flag?-num:num; 21 } 22 inline void ready() 23 { 24 cnt=0; 25 for(int i=1;i<=mod;i++)fa[i]=i; 26 for(int i=1;i<=mod;i++)rank[i]=1; 27 } 28 inline int find(int x) 29 {return fa[x]==x?x:fa[x]=find(fa[x]);} 30 inline void merge(int x,int y) 31 { 32 if(rank[x]<rank[y]){ 33 fa[x]=y;} 34 else{ 35 fa[y]=x; 36 if(rank[x]==rank[y])rank[x]++;} 37 } 38 inline int work() 39 { 40 for(int i=1;i<=n;i++){ 41 int x=read();int y=read();int e=read(); 42 x%=mod;y%=mod; 43 if(e)merge(find(x),find(y)); 44 else{a[++cnt].x=x;a[cnt].y=y;} 45 } 46 bool flag=true; 47 for(int i=1;i<=cnt;i++) 48 if(find(a[i].x)==find(a[i].y)) 49 {flag=false;break;} 50 if(flag)puts("YES"); 51 else puts("NO"); 52 } 53 int main() 54 { 55 T=read(); 56 while(T--){ 57 n=read(); 58 ready();work();} 59 return 0; 60 }
洛谷P1955 [NOI2015] 程序自动分析 [并查集,离散化]
标签:tps 大写 family algorithm || 第一个 bool 要求 out
原文地址:https://www.cnblogs.com/cytus/p/8933356.html