标签:pre 结果 分享图片 eve 成功 需要 阅读 依次 tar
邻接矩阵创建无向网:
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
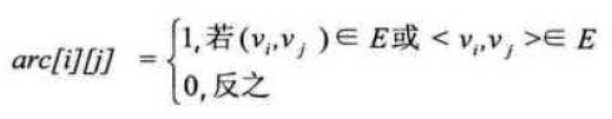
我们来看一个实例,图7-4-2的左图就是一个无向图。
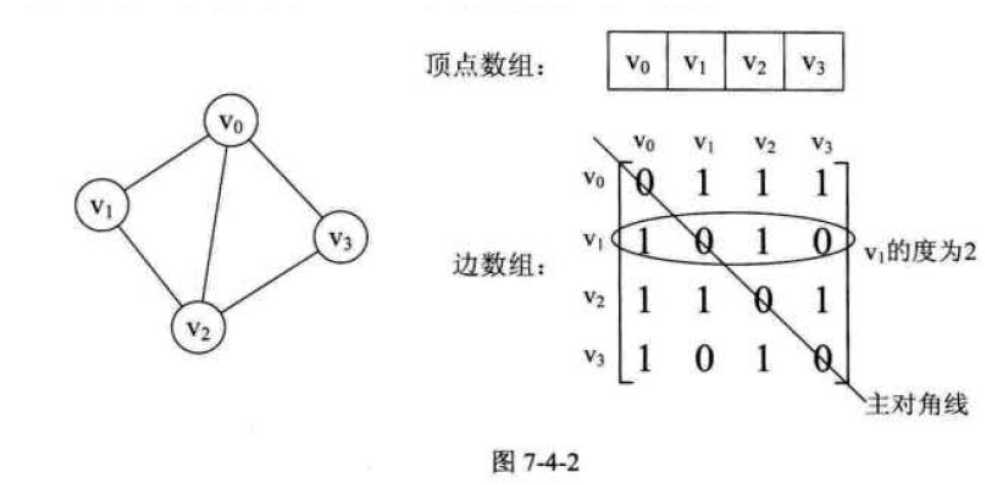
我们再来看一个有向图样例,如图7-4-3所示的左图。
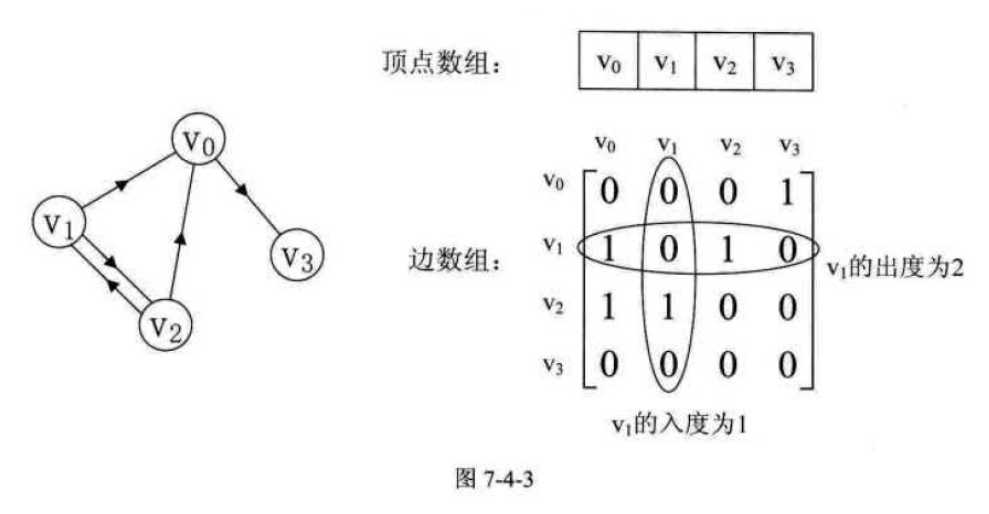
在图的术语中,我们提到了网的概念,也就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。
设图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
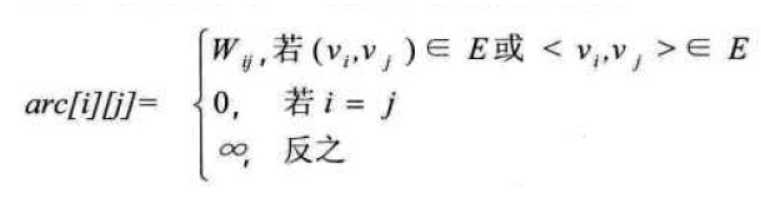
如图7-4-4左图就是一个有向网图。
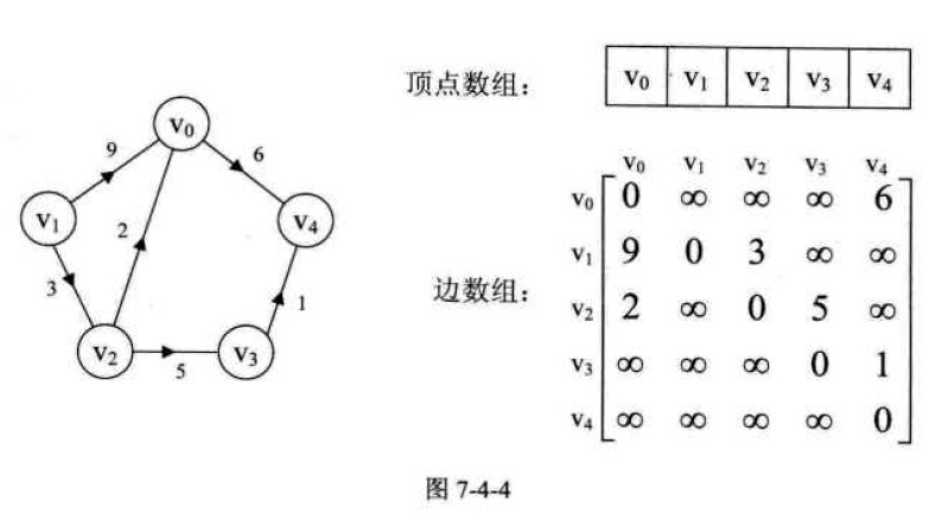
下面示例无向网图的创建代码:
1 #include "stdafx.h" 2 #include<iostream> 3 #define MaxInt 10000 //表示权值的无穷 4 #define MVNum 100 //最大顶点数,应由用户定义 5 typedef char VerTexType; //假设顶点数据类型为字符型 6 typedef int ArcType; //假设边的权值类型为整形 7 using namespace std; 8 typedef struct 9 { 10 VerTexType vexs[MVNum]; //顶点表 11 ArcType arcs[MVNum][MVNum]; //邻接矩阵 12 int vexnum, arcnum; //图的当前点数和边数 13 }AMGraph; 14 15 void CreateUDN(AMGraph &G) //采用邻接矩阵表示法,创建无向网&G 16 { 17 int i, j, w; 18 cout << "请输入总顶点数、总边数(空格隔开):" << endl; 19 cin >> G.vexnum >> G.arcnum; //输入总顶点数、总边数 20 cout << "请输入顶点信息(空格隔开):" << endl; 21 for (i = 0; i < G.vexnum; i++) //依次输入点的信息 22 { 23 cin >> G.vexs[i]; 24 } 25 for (i = 0; i < G.vexnum; i++) //初始化邻接矩阵,编的权值均为极大值MaxInt 26 for (j = 0; j < G.vexnum; j++) 27 G.arcs[i][j] = MaxInt; 28 29 for (int k = 0; k < G.arcnum; k++) //构造邻接矩阵 30 { 31 cout << "请输入第" << k + 1 << "条边的信息(输入顺序:连接点1编号,连接点2编号,边的权值):" << endl; 32 cin >> i >> j >> w; //输入一条边依附的顶点及权值 33 G.arcs[i - 1][j - 1] = w; 34 G.arcs[j - 1][i - 1] = G.arcs[i - 1][j - 1]; 35 } 36 } 37 38 void coutAMGraph(AMGraph &G) //无向网的输出 39 { 40 int i, j; 41 cout << "该图的邻接矩阵为:" << endl; 42 cout << "\t"; 43 for (i = 0; i < G.vexnum; i++) 44 cout << G.vexs[i] << "\t"; 45 cout << endl; 46 for (i = 0; i < G.vexnum; i++) 47 { 48 cout << G.vexs[i] << "\t"; 49 for (j = 0; j < G.vexnum; j++) 50 { 51 cout << G.arcs[i][j] << "\t"; 52 } 53 cout << endl; 54 } 55 } 56 int main() 57 { 58 AMGraph MG; 59 CreateUDN(MG); 60 coutAMGraph(MG); 61 return 0; 62 }
输出结果:
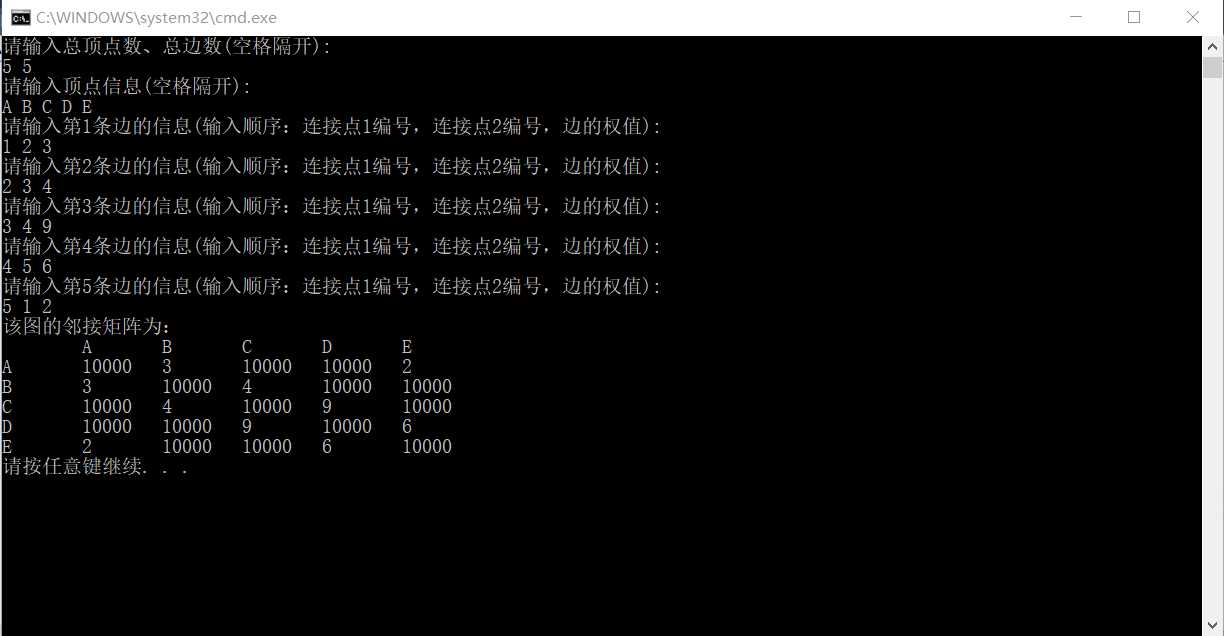
邻接表创建无向网:


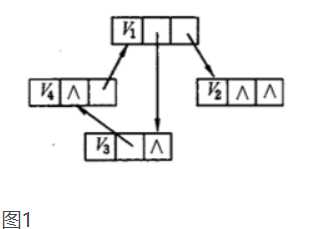
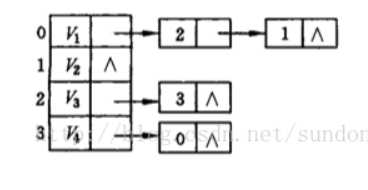
1 #include "stdafx.h" 2 #include<iostream> 3 #include<string> 4 using namespace std; 5 #define MVNum 100 //最大顶点值 6 #define ERROR 1 7 typedef char VerTexType; 8 typedef struct ArcNode //边结点 9 { 10 int adjvex; //改变所指向的顶点的位置 11 struct ArcNode *nextarc; //指向下一条边的指针 12 string info; //和边相关的信息 13 }ArcNode; 14 typedef struct VNode //顶点信息 15 { 16 VerTexType data; 17 ArcNode *firstarc; //指向第一条依附该顶点的边的指针 18 }VNode, AdjList[MVNum]; //AdList表示邻接表类型 19 typedef struct //邻接表 20 { 21 AdjList vertices; 22 int vexnum, arcnum; //图的当前顶点数和边数 23 }ALGraph; 24 25 int LocateVex(ALGraph &G, char &v1) //定位函数 26 { 27 int i; 28 for (i = 0; i < G.vexnum; i++) 29 { 30 if (G.vertices[i].data == v1) 31 return i; 32 } 33 if (i >= G.vexnum) 34 return ERROR; 35 else 36 return 0; 37 } 38 void CreateUDG(ALGraph &G) //创建无向图 39 { 40 ArcNode *p1, *p2; 41 int i, j, k; 42 char v1, v2; 43 cout << "请输入图的顶点数、弧数:" << endl; 44 cin >> G.vexnum >> G.arcnum; //输入总顶点数,总边数 45 cout << "请输入顶点:" << endl; 46 for (i = 0; i < G.vexnum; i++) 47 { 48 cin >> G.vertices[i].data; //输入顶点值 49 G.vertices[i].firstarc = NULL; //初始化表头结点的指针域为NULL 50 } 51 for (k = 0; k < G.arcnum; k++) 52 { 53 cout << "请输入弧尾和弧头:"; 54 cin >> v1 >> v2; //输入各边,构造邻接表 55 i = LocateVex(G, v1); 56 j = LocateVex(G, v2); 57 p1 = new ArcNode; //生成一个新结点*p1 58 p1->adjvex = j; //邻接点序号为j 59 p1->nextarc = G.vertices[i].firstarc; 60 G.vertices[i].firstarc = p1; 61 p2 = new ArcNode; 62 p2->adjvex = i; 63 p2->nextarc = G.vertices[j].firstarc; 64 G.vertices[j].firstarc = p2; 65 } 66 cout << "图构建成功!" << endl; 67 } 68 69 void coutUDG(ALGraph G) //输出函数 70 { 71 int i, j; 72 cout << "输出为:" << endl; 73 for (i = 0; i<G.vexnum; i++) 74 { 75 cout << i; 76 ArcNode *p; 77 p = G.vertices[i].firstarc; 78 while (p != NULL) 79 { 80 cout << "-> " << p->adjvex; 81 p = p->nextarc; 82 } 83 cout << endl; 84 } 85 } 86 int main() 87 { 88 ALGraph MG; 89 CreateUDG(MG); 90 coutUDG(MG); 91 return 0; 92 }
输出结果:

今天就先到这里啦,下一篇再写十字链表和邻接多重表哈!
标签:pre 结果 分享图片 eve 成功 需要 阅读 依次 tar
原文地址:https://www.cnblogs.com/Trojan00/p/8948354.html