标签:log 结构 现在 strong 分类器 font detail 有一个 图片
AdaBoost是一种迭代型的算法,其核心思想是针对同一个训练集训练不同的学习算法,即弱学习算法,然后将这些弱学习算法集合起来,构造一个更强的最终学习算法。
用于二分类或多分类的应用场景
在AdaBoost算法中,有两个权重,第一个数训练集中每个样本有一个权重,称为样本权重,用向量D表示;另一个是每一个弱学习算法具有一个权重,用向量α表示。
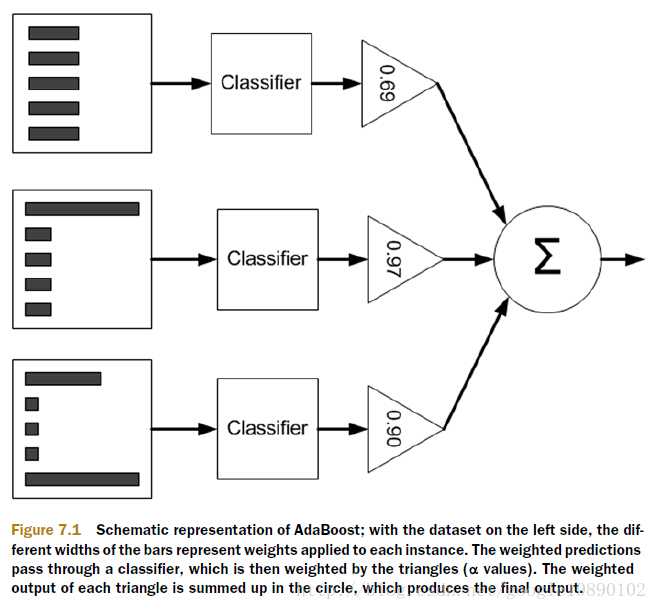
图左边不同长度的黑色条块表示每个样本的权重D,之后经过不同权重的弱分类器(权重为a),最后把所有弱分类器的输出求和,用sign函数按结果正负确定分类
训练过程
Adaboost采用迭代的思想,每次迭代只训练一个弱分类器,训练好的弱分类器将参与下一次迭代的使用。也就是说,在第N次迭代中,一共就有N个弱分类器,其中N-1个是以前训练好的,其各种参数都不再改变,本次训练第N个分类器。其中弱分类器的关系是第N个弱分类器更可能分对前N-1个弱分类器没分对的数据,最终分类输出要看这N个分类器的综合效果。
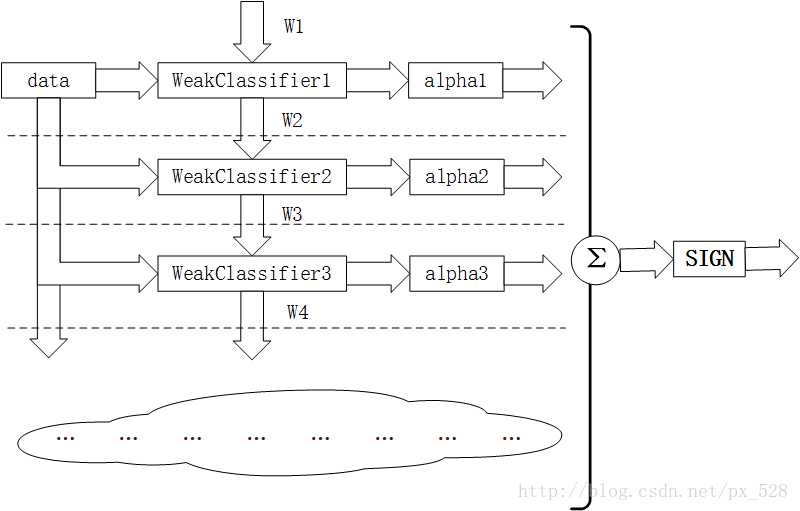
如图所示为Adaboost分类器的整体结构。从右到左,可见最终的求和与符号函数,再看到左边求和之前,图中的虚线表示不同轮次的迭代效果,第1次迭代时,只有第1行的结构,第2次迭代时,包括第1行与第2行的结构,每次迭代增加一行结构,图下方的“云”表示不断迭代结构的省略。
第i轮迭代要做这么几件事:
1. 新增弱分类器WeakClassifier(i)与弱分类器权重alpha(i)
2. 通过数据集data与样本权重W(i)训练弱分类器WeakClassifier(i),并得出其分类错误率,以此计算出其弱分类器权重alpha(i)
3. 通过加权投票表决的方法,让所有弱分类器进行加权投票表决的方法得到最终预测输出,计算最终分类错误率,如果最终错误率低于设定阈值(比如5%),那么迭代结束;如果最终错误率高于设定阈值,那么更新数据权重得到W(i+1)
Adaboost一般使用单层决策树作为其弱分类器。单层决策树是决策树的最简化版本,只有一个决策点,也就是说,如果训练数据有多维特征,单层决策树也只能选择其中一维特征来做决策,并且还有一个关键点,决策的阈值也需要考虑。
刚刚已经介绍了单层决策树的原理,这里有一个问题,如果训练数据保持不变,那么单层决策树找到的最佳决策点每一次必然都是一样的,为什么呢?因为单层决策树是把所有可能的决策点都找了一遍然后选择了最好的,如果训练数据不变,那么每次找到的最好的点当然都是同一个点了。
所以,这里Adaboost样本权重就派上用场了,所谓“样本权重主要用于弱分类器寻找其分类误差最小的点”,其实,在单层决策树计算误差时,Adaboost要求其乘上权重,即计算带权重的误差。
举个例子,在以前没有样本权重时(其实是平局权重时),一共10个点时,对应每个点的权重都是0.1,分错1个,错误率就加0.1;分错3个,错误率就是0.3。现在,每个点的权重不一样了,还是10个点,权重依次是[0.01,0.01,0.01,0.01,0.01,0.01, 0.01,0.01,0.01,0.91],如果分错了第1一个点,那么错误率是0.01,如果分错了第3个点,那么错误率是0.01,要是分错了最后一个点,那么错误率就是0.91。这样,在选择决策点的时候自然是要尽量把权重大的点(本例中是最后一个点)分对才能降低误差率。由此可见,权重分布影响着单层决策树决策点的选择,权重大的点得到更多的关注,权重小的点得到更少的关注。
在Adaboost算法中,每训练完一个弱分类器都就会调整样本权重,上一轮训练中被误分类的点的权重会增加,在本轮训练中,由于样本权重影响,本轮的弱分类器将更有可能把上一轮的误分类点分对,如果还是没有分对,那么分错的点的权重将继续增加,下一个弱分类器将更加关注这个点,尽量将其分对。
这样,达到“你分不对的我来分”,下一个分类器主要关注上一个分类器没分对的点,每个分类器都各有侧重。
adaboost算法流程

其中
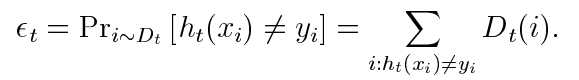
Dt就是样本权重。错误由弱学习器训练出的Dt衡量。在求Dt+1时,增加分类错误样本的权重,减小分类正确的权重,让算法更关注分类错误的样本
二分类问题的训练误差界
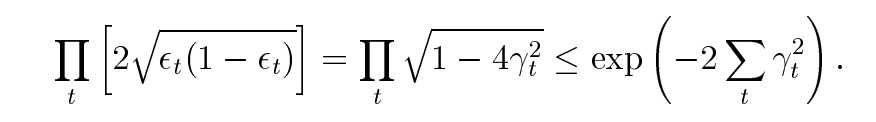
γt表示模型预测结果相比于随机预测正负更准确的程度
由于Adaboost中若干个分类器的关系是第N个分类器更可能分对第N-1个分类器没分对的数据,而不能保证以前分对的数据也能同时分对。所以在Adaboost中,每个弱分类器都有各自最关注的点,每个弱分类器都只关注整个数据集的中一部分数据,所以它们必然是共同组合在一起才能发挥出作用。所以最终投票表决时,需要根据弱分类器的权重来进行加权投票,权重大小是根据弱分类器的分类错误率计算得出的,总的规律就是弱分类器错误率越低,其权重就越高。
关于最终的加权投票表决,举几个例子:
比如在一维特征时,经过3次迭代,并且知道每次迭代后的弱分类器的决策点与发言权,看看如何实现加权投票表决的。
如图所示,3次迭代后得到了3个决策点,
最左边的决策点是小于(等于)7的分为+1类,大于7的分为-1类,且分类器的权重为0.5;
中间的决策点是大于(等于)13的分为+1类,小于13分为-1类,权重0.3;
最右边的决策点是小于(等于19)的分为+1类,大于19分为-1类,权重0.4。
对于最左边的弱分类器,它的投票表示,小于(等于)7的区域得0.5,大与7得-0.5,同理对于中间的分类器,它的投票表示大于(等于)13的为0.3,小于13分为-0.3,最右边的投票结果为小于(等于19)的为0.4,大于19分为-0.4,如下图:
求和可得:
最后进行符号函数转化即可得到最终分类结果:
也就是说根据每个弱分类器的决策阈值和它对应的权重,再求和取符号,我们就可以知道每个阈值区间的样本的分类
更复杂的例子见参考链接
adaboost可以用别的弱分类器,不仅仅是决策树
1、带多路输出的模型,比如直接softmax
2、n个1 vs n-1的二分类
标签:log 结构 现在 strong 分类器 font detail 有一个 图片
原文地址:https://www.cnblogs.com/34fj/p/8793642.html