标签:hat stanford array 误差 play 二分 算法 模型 中间
又到了一节很重要的课,因为这个学习理论是从统计角度为机器学习算法提供了一个理论基础。
先回顾一下我们第一节课提到的机器学习的组成:
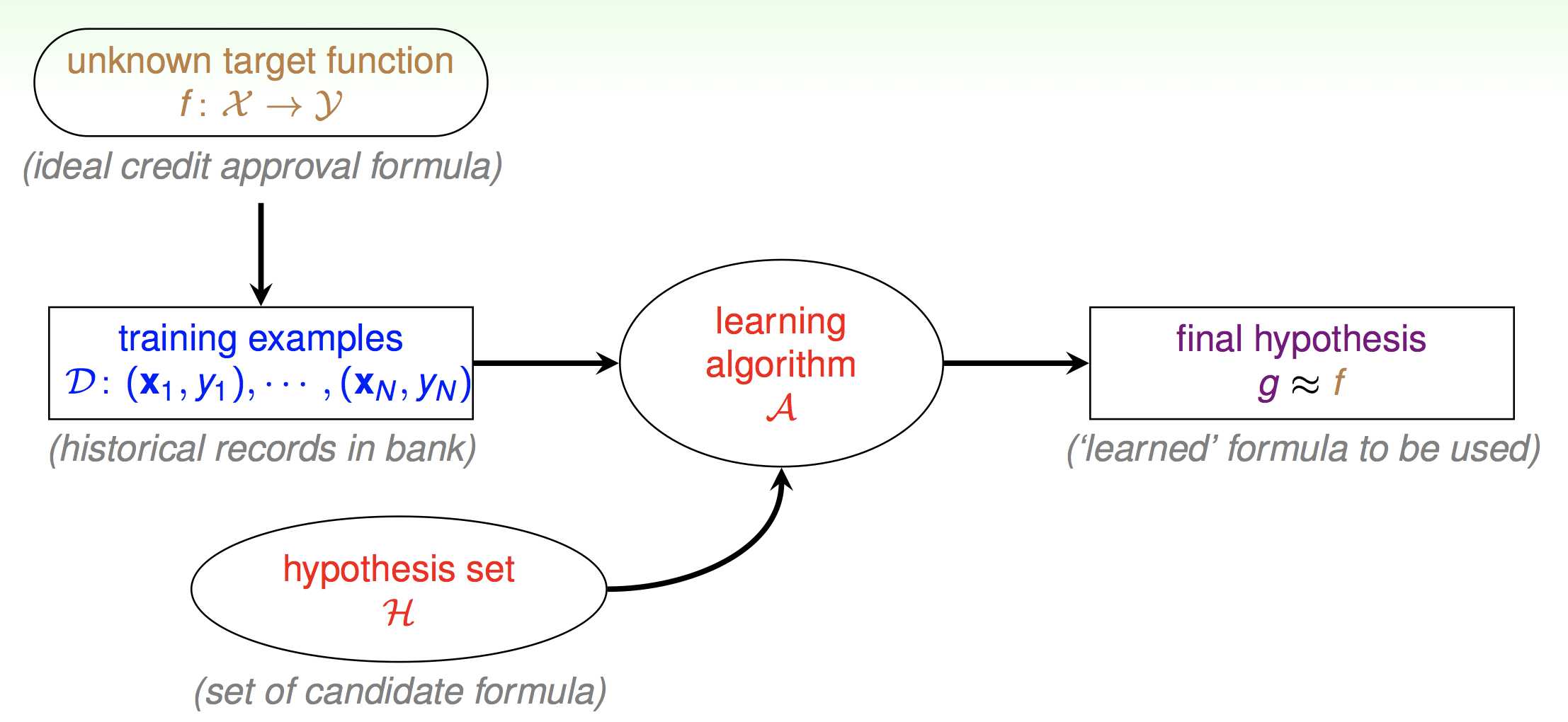
第一节课只是简单的提了一下,现在我们要真正来分析这张图了。首先机器学习的最终目的就是得到真正的映射f,但是f我们无法得到,所以拿一个g去拟合。这是什么意思呢。就比如说你高考,会刷很多的习题,有很多次的模拟考。但是最终最终的目的都是为高考取得一个好成绩。那么这里也是一样的,如果你开始就拿到了高考的考卷,那你还刷什么习题,直接背高考的考卷不就完了吗。但是我们拿不到真实的考卷,所以我们刷习题。但是这里就两个问题了。第一,你模拟考考了600分就代表你高考真的能考600分么。也就是说我们怎么保证我们估计出来的g与真实分布的f相接近呢。第二,我们如何在模拟考中取得好成绩呢。也就是说如何让g表现得尽量好呢。
首先我们先明确一个概念叫泛化误差,也就是我们模型在真实分布下的误差。或者说最终高考成绩的真实成绩。
给定样本集描述:
\((x,y)\in D, x\in R^n, y\in \{0,1\}\)
我们来回归一下基本的机器学习流程。
这里以最简单的二分类模型为例,即我们之前提到的感知机算法:
\[
h(x)= \begin{cases}
+1 & \theta^Tx \ge 0 \-1 & \theta^Tx \lt 0
\end{cases}
\]
所以假设集也可以表示为
\[
\mathcal { H } = \left\{ h _ { \theta } : h _ { \theta } ( x ) = 1\left\{ \theta ^ { T } x \geq 0\right\} ,\theta \in \mathbb { R } ^ { n + 1} \right\}
\]
\[
\hat { \varepsilon } ( h ) = \frac { 1} { m } \sum _ { i = 1} ^ { m } 1\left\{ h \left( x ^ { ( i ) } \right) \neq y ^ { ( i ) } \right\}
\]
那么误差就是在样本中被误分类的点。这个误差我们一般称之为训练误差,或者经验误差,或者经验风险。
那么与经验误差对应的就是泛化误差了:
\[
\varepsilon ( h ) = P _ { ( x ,y ) \sim \mathcal { D } } ( h ( x ) \neq y )
\]
既然我们没法衡量泛化误差,那么就求经验误差最小,于是得到最终的假设函数的参数就是:
\[
\hat { \theta } = \arg \min _ { \theta } \hat { \varepsilon } \left( h _ { \theta } \right)
\]
我们一般把这种算法称之为经验风险最小。
我们基于现有的数据已经得到最好的模型,那我们怎么确定他在新的数据下也能表现得很好呢。
这里我们给出一条引理:
如果你有m个随机变量Z遵循独立同分布(i.i.d)那么有:
\[
\left.\begin{array} { c } { Z _ { 1} ,\ldots ,Z _ { m } ( i .i .d ) \sim \text{ Bernoulli } ( \phi ) } \\ { \hat { \phi } = ( 1/ m ) \sum _ { i = 1} ^ { m } Z _ { i } } \end{array} \right.
\]
可以得到Hoe?ding不等式:
\[
P ( | \phi - \hat { \phi } | > \gamma ) \leq 2\exp \left( - 2\gamma ^ { 2} m \right)
\]
这条不等式的正确性基本的概率论书上都有讲。\(\hat\phi\)是一个估计量,\(\phi\)真实参数的值,\(\gamma\)表示置信度。
带入我们的经验误差与泛化误差:
\[
P \left( | \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) \leq 2\exp \left( - 2\gamma ^ { 2} m \right)
\]
这条公式给出了经验误差与泛化误差的差距的上界。也就是说随着样本数量的增加,经验误差一定会趋向于泛化误差。这相当于给了我们保证,我们在训练集上训练一个模型,这个模型在训练集上的表现和在新数据下的表现会随着样本数量的增多趋向于一致。
注意这里是趋向一致。就是经验误差大那么泛化也跟着大,经验误差小,泛化误差也跟着小。但我们实际上想要得到是一个泛化误差小的模型。
还有一点注意这是对于某一个假设h,但是其实我们可以推广到任意假设h。
再给出第二条引理:
\[
P \left( A _ { 1} \cup \ldots \cup A _ { k } \right) \leq P \left( A _ { 1} \right) + \ldots + P \left( A _ { k } \right)
\]
另\(P \left( A _ { i } \right) \leq 2\exp \left( - 2\gamma ^ { 2} m \right)\)
于是我们可以对h进行推广:
\[
\left.\begin{aligned} P \left( \exists h \in \mathcal { H } . | \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) & = P \left( A _ { 1} \cup \cdots \cup A _ { k } \right) \\ & \leq \sum _ { i = 1} ^ { k } 2\exp \left( - 2\gamma ^ { 2} m \right) \\ & \leq \sum _ { i = 1} ^ { k } 2\exp \left( - 2\gamma ^ { 2} m \right) \\ & = 2k \exp \left( - 2\gamma ^ { 2} m \right) \end{aligned} \right.
\]
注意这里最后多了个k,即假设空间的大小。
通过上面那边的推导我们已经知道了对于特定的h,只要样本数量足够大,那么泛化误差和经验误差趋于一致。而且把这个结论推广到了任意的假设h。但是我们怎么保证模型泛化误差小呢。
首先经验误差最小的假设\(h_i\)肯定是\(\mathcal { H }\)中的一个,所以其实我只要让\(\mathcal { H }\)空间变大,这也就意味着模型更复杂。即可增大找到经验误差最小假设的概率。如果还是不大清楚的话可以往下到图像直觉一节。
那么我们的两个问题:
都有了答案。
于是这是不是代表我们只要数据量越大,假设空间越大就一定可以很好的模型呢。
实际上并不是这样的,回顾一下我们推导经验误差和泛化误差一致性的第二条式子:
\[
P \left( \exists h \in \mathcal { H } .| \varepsilon \left( h _ { i } \right) - \hat { \varepsilon } \left( h _ { i } \right) | > \gamma \right) \leq 2k \exp \left( - 2\gamma ^ { 2} m \right)
\]
当右边不等式中的k也就是假设空间的大小增大的时候,我们经验误差和泛化误差一致性的上界也就会变大,也就是说模型越复杂的话越不能保证经验误差和泛化误差的一致性。
所以就有了偏差-方差权衡(bias-variance tradeoff),也就是模型的复杂性其实是一把双刃剑,一方面让我们增大了找到更小经验误差模型的可能性,但是另一方面就不能保证经验误差和泛化误差的一致性了。
于是我们的泛化误差其实就可以分为两部分:
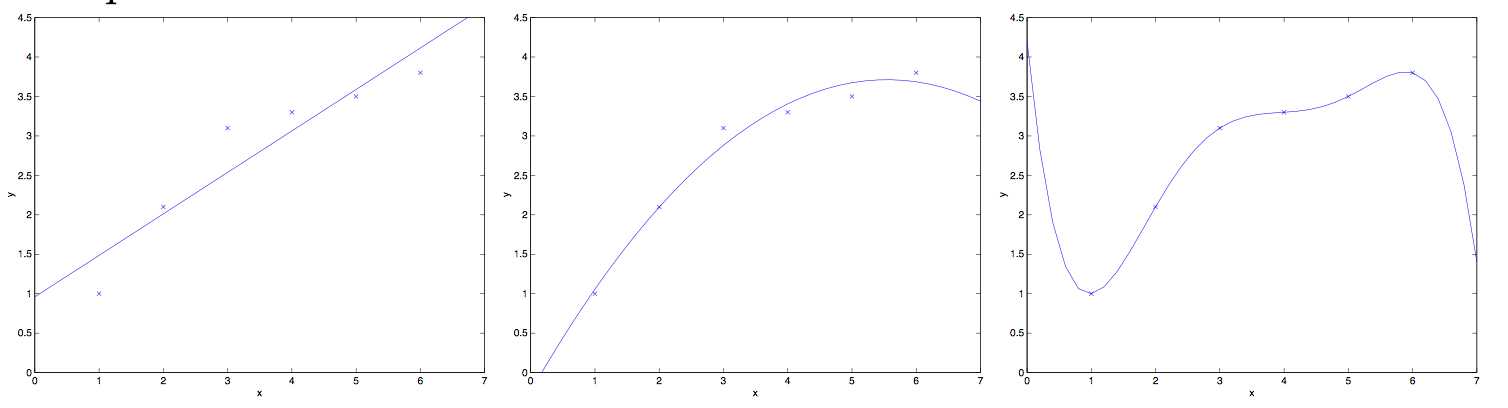
一般来说中间这幅图是比较理想的情况。
左边这幅图就是偏差过大的情况,也称之为欠拟合。因为模型太简单,数据再多也救不了,虽然保证了经验误差和泛化误差的一致性,但是经验误差表现得实在是太差了,那么泛化误差也会很大。
右边这幅图就是方差过大的情况,也称之为过拟合。由于模型过于复杂,虽然说每个数据都拟合上了,经验误差很小,但是不能保证泛化误差也很小。
标签:hat stanford array 误差 play 二分 算法 模型 中间
原文地址:https://www.cnblogs.com/nevermoes/p/cs229_part4.html