SVM清晰讲解__线性可分问题

标签：平面   get   lock   inf   方法   targe   详细   集合   直线   

转载作者：liangdas

引言：

       1995年Cortes和Vapnik于首先提出了支持向量机(Support Vector Machine)，由于其能够适应小样本的分类，分类速度快等特点，性能不差于人工神经网络，所以在这之后，人们将SVM应用于各个领域。大量使用SVM模型的论文不断涌现，包括国内和国外。

       但是，直到现在，很少能见到一个能对SVM的原理准确，详细，通俗，严谨阐述的论文或者资料，所以决定查阅很多的资料，结合自己的思考和理解，来写一篇关于SVM的系列文章。

线性可分问题：

       在分类问题中，最简单的分类就是二分类问题，而且这个二分类问题是一个线性可分问题。那么对于一个线性二分类问题，它的目标函数是什么呢?确定目标函数之后，我们又用什么方法来求解呢？

       在一维空间，也就是一个坐标轴上面，要分开两个可以分开的点集合，我们只需要找到一个点，如图1：

图1 一维线性可分示意图

 　　在二维空间中，要分开两个线性可分的点集合，我们需要找到一条分类直线即可，如图2：

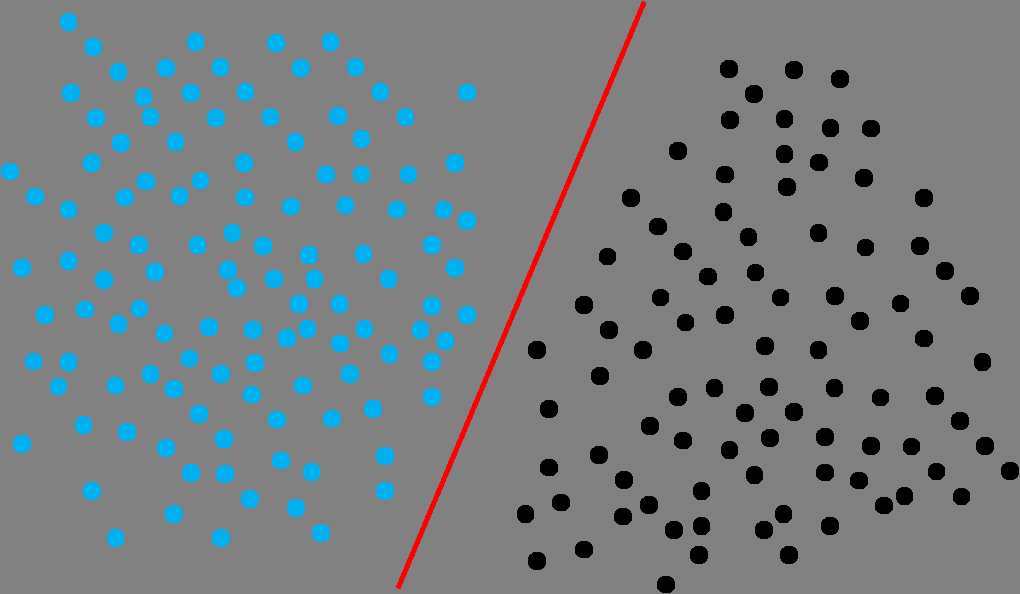
图2 二维线性可分示意图

　　在三维空间中，要分开两个线性可分的点集合，我们需要找到一个分类面:如图3：

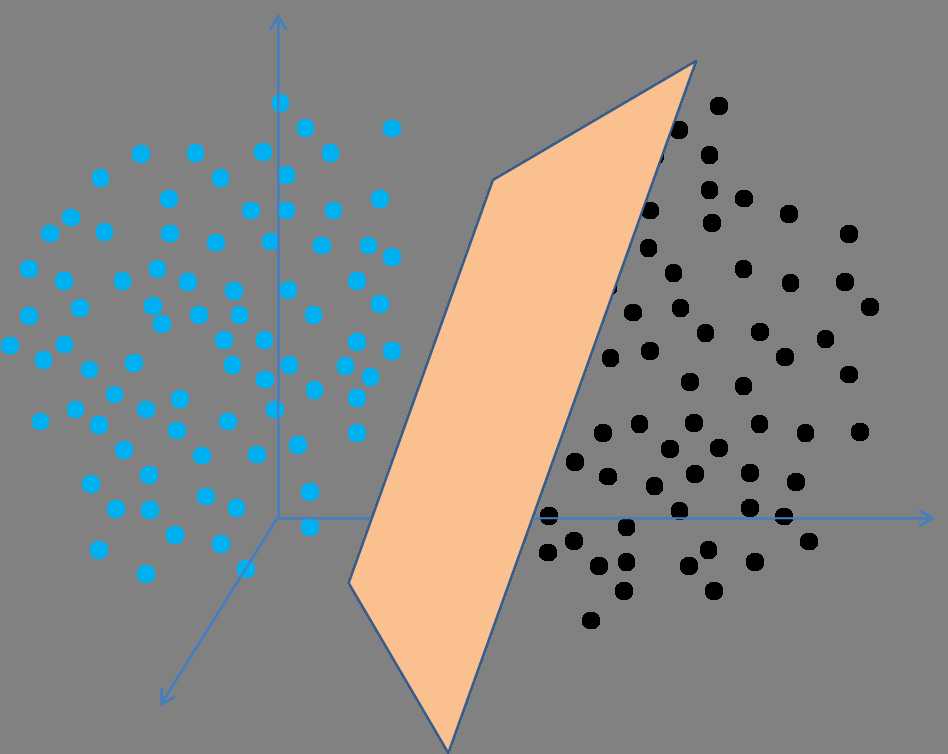
图3 三维线性可分示意图

 　　在n维空间中，要分开两个线性可分的点集合，我们需要找到一个超平面（Hyper Plane）。

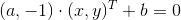
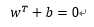为了直观，我们以上面二维空间为例子来分析：在图2中分布着两类点：淡蓝色和黑色的点，分别代表着不同的两个类别，显然，我们可以找到一条直线来把这两类点分开，高中的时候，常见的直线方程表达式是y=ax+b，我们现在用向量来表示，就是：，把向量（a，-1）用向量符号w来表示，维数向量（x，y）用向量符号x（此时的x是一个向量）来表示，那么直线方程就变成了。

目标函数：

       再次观察图2，可以知道，在这个二维平面中，可以把两类点的分开的直线有很多条，如图4所示，那么这些直线中，哪一条才是最好的呢？也就是如何选择出一条最好的直线呢？

 图4 多条分类直线

　　在图4中，我们先看淡蓝色的点，如果这些点到分类直线的距离越大，分类直线也就越远离蓝色的点，那么再来一个新的点，如果这个点是依照淡蓝色点集合的特性产生的（也就是它不是一个相对于蓝色点集合很奇异的点），那么这个点也很可能和蓝色的点集合一样，分布在直线的同一侧。分布在同一侧，表明它和蓝色集合点属于同一个类别。用同样的思想，图4中，对于黑色的集合点，这条分类直线离它们的距离也要越远越好。所以找最优分类线，就是要找到这条一条直线，使它到两个类别点的距离越大越好。

       回忆一下高中所学的点到直线的距离公式：直线（一般式）：Ax＋By＋C＝0另外一个点的坐标(x0, y0)，那么这点到这直线的距离就是：

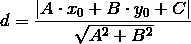
　　那么，对于直线wx+b=0的形式，如果有一个点x，那么它到直线的距离公式就是，把向量写成二范数的形式，即是：

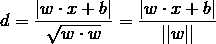
　　所以上面的二维线性可分问题的目标函数就可以抽象成如下的数学表达式：

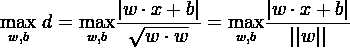
目标函数的简化：

       对于一个待分类类别，为了自己的类别能准确地分类,都希望分类直线到自己的距离大些，当有两类的时候,就会形成相互竞争，最后的竞争结果就是让这条分类直线，到两个类别的距离相等，在生活中，通常也是这样达到一种平衡状态的。

       如图5，我们作两条直线，和分类直线平行，让这两条直线分别经过下面蓝色和黑色集合的边界，同时，满足这两条直线到中间分类直线的距离相等，那么，我们可以假定这两条直线方程分别是wTx+b=c, wTx+b=-c。

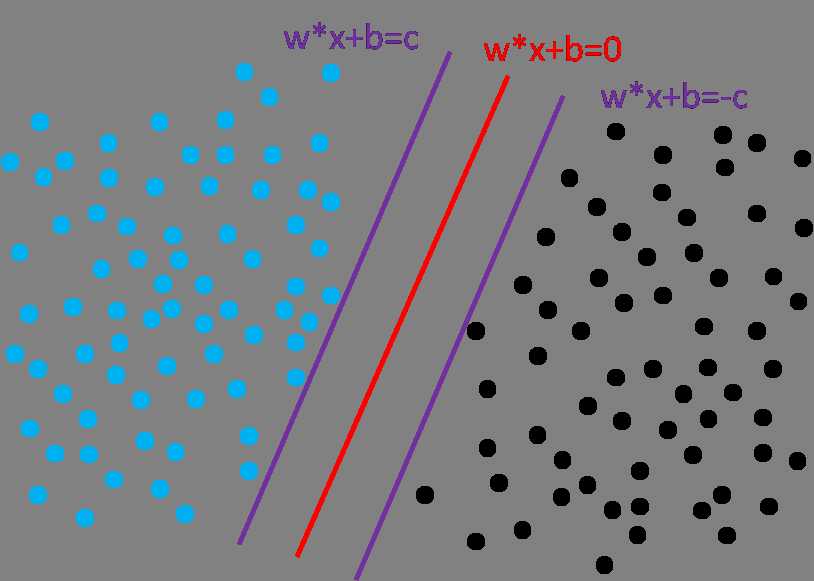
 图5 两类别到分类直线的距离相等

用两条平行直线的距离计算公式， 那么，两个类别集合到分类直线的最近距离，这个公式，其实和上面点到直线的距离公式是一样的。

对于一条直线，wx+b=c，我们相应的成比例的缩小他们的系数，如变成，这条直线和原来的直线还是同一条直线。现在把它变成，新的直线还是和以前直线是同一条直线，也就是说，对于直线wx+b=c，我们总可以找到另外的一条新的 w1=w/c, b1=b/c，使w1*x+b1=1, 而且这两条直线其实表达的是同一条直线，这样的话，上面的图5可以变成如下的图6：

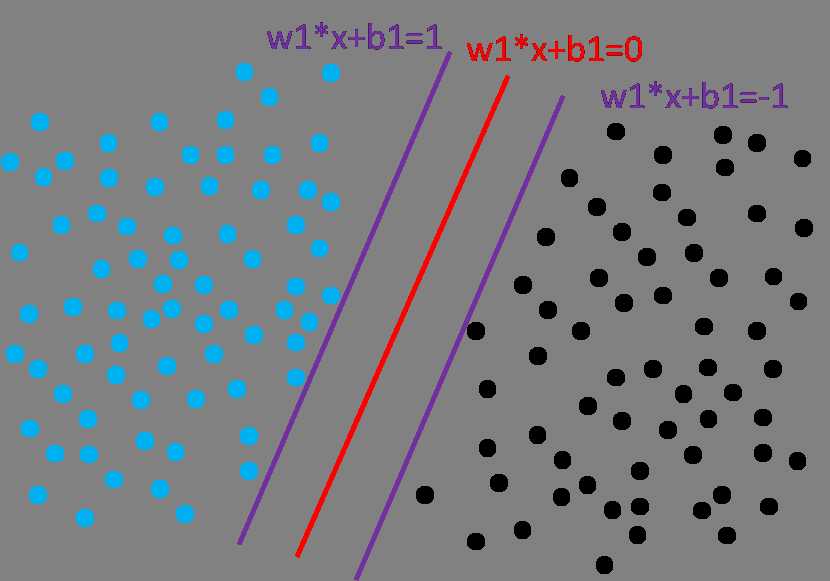
图6 两类别到分类直线的距离相等

 　　从图6中，结合我们要寻找的最优分类直线，是到两类类别点集合的距离最大的直线的思想，我们可以抽象出此时的目标函数： 

        这样，这个目标函数看起来就比原来简洁多了。

目标函数的约束条件：

       在图6中，对蓝色样本点而言，不在w1*x+b1=1直线上的点，一定是在直线上面的点，它们满足w1*x+b1>1，所以对所有的蓝色样本点而言，它们都满足w1*x+b1>=1；同理，对所有黑色的样本点，都是满足w1*x+b1<=-1。这两个条件是我们求解的限制条件，也就是我们寻找上面的目标函数的时候，必须满足上面的两个不等式约束。

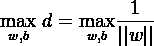                      满足条件：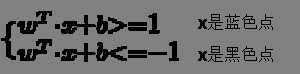

观察上面的不等式条件表达式，是不是有一种想把两个式子合并成一个式子的冲动？其实，上面蓝色点对应的不等式，我们在不等式两边同时乘以一个y=1；同理，黑色点对应的不等式，在式子两边同时乘以一个y=-1， 那么上面的两个式子可以变成 。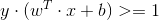

       但是，为什么可以在一个不等式的两边乘以一个1，而另外一个乘以-1呢？我们来看蓝色点对应的不等式，式子左边是样本点的维度向量x的表达式，对于一些训练样本点，它们还有一个已知的类别标记量label，这里我们把它叫做y，这样的话，对蓝色点的y值，我们人为将其定为1，而对黑色点的y值，我们将其定为-1，所以，对上面的两个不等式，分别在不等式的两边乘以类别值y，我们就可以自然将两个不等式合并成上面的那一个不等式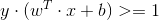了。这也是为什么我们在生成SVM训练样本的时候，将两个类别分别定义成1和-1的原因！

       到这里，我们目标函数可以写成：

       这样的一个目标函数是一个带不等式约束条件的优化问题，它怎么来求解呢？后面一章节来继续讲解这个问题。

SVM清晰讲解__线性可分问题

标签：平面   get   lock   inf   方法   targe   详细   集合   直线   

原文地址：https://www.cnblogs.com/fuqia/p/8963429.html