二分搜索专题（1）

标签：lse   bubuko   style   长度   描述   res   有一个   http   总结   

1.考察要点

1.二分搜索不仅在有序序列中可以运用，无序序列也同样适用，只要满足每次查找都会缩小一半查找范围。

2.注意循环初始条件，边界值，划分点的处理，确保循环不会无法终止。

3.划分点的经典写法：(p+r)/2 ，安全写法：r-(r-p)/2或p+(r-p)/2

2.局部最小值问题

　　问题描述：在一个无序序列中，且任意两个相邻元素都不相等的情况下，查找满足arr[i]<arr[i+1]且arr[i]<arr[i-1]的元素。

　　查找方法：

　　　　1.arr为空或长度为1时返回。

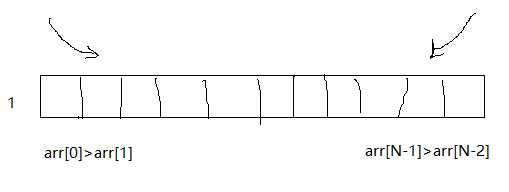
　　　　2.判断两端点的情况

　　　　　　如果端点值中有一个端点是局部最小值，则立即返回。

　　　　3.端点两边都不是局部最小，如下，讨论中间点mid。

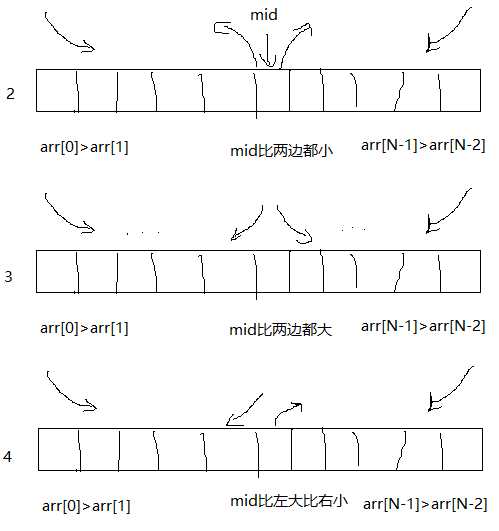
　　　　4.中间点的情况

　　　　　　1.当属于情况2时，直接返回mid.

　　　　　　2.否则，如3的两边，4的左边，比存在局部最小值，因为相邻元素不同，以4的左边为例，

　　　　　　在mid的左边，一旦出现上升点，则此点局部最小，否则若一直向左降序，则arr[1]为局部最小值。

　　　　　　3.未画出的情况5参考情况4。

 3.含有重复元素的有序数组问题

 　　问题描述：给定有序数组arr,num,查找num在arr中出现的最左的位置。

　　 举例分析：num=3，arr={1,2,3,3,4,4,4,4,4}

　　　　　　　1.初始状态：res=-1,arr={1,2,3,3,4,4,4,4,4}

　　　　　　　2.mid=4,arr={1,2,3,3},res=-1;

　　　　　　　3.mid=2,arr={3,3},res=-1;

　　　　　　　4.mid=3左,arr={}，返回res=2.

　　　总结：维护一个res，当找到num时，继续向左找，直到要找部分为空。

附一个查找最右元素的代码　　

int BinarySearch1(int arr[],int p,int r,int target,int res)
{
    if(p>r) return res;
    int q=(p+r)/2;
    if(arr[q]==target) return BinarySearch1(arr,q+1,r,target,q);
    else if(arr[q]<target) return BinarySearch1(arr,q+1,r,target,res);
    else return BinarySearch1(arr,p,q-1,target,res);
}

二分搜索专题（1）

标签：lse   bubuko   style   长度   描述   res   有一个   http   总结   

原文地址：https://www.cnblogs.com/lshao/p/8970563.html