标签：uri 泛化 错误 如何 决策 学习心得 class 提高 machine
前言：
这是一篇记录渣本学习机器学习过程的随笔。
正文：
支持向量机(SVM)是一组用于分类， 回归和异常值检测的监督学习方法。
在分类问题中，SVM就是要找到一个同时离各个类别尽可能远的决策边界即最大化margin（margin为图中2虚线的距离）。这种尽可能远的思想能够提高模型的泛化能力。
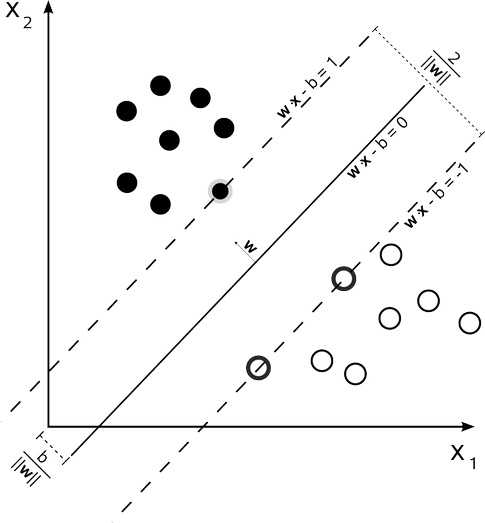
虚线上的点是支持向量,实线是决策边界。此图为线性可分的情况。
求margin的最大值就相当于求d（支持向量到决策边界的距离）的最大值。
决策边界为wx-b=0
任意点
到边界的距离为
为了方便计算，我们将2个类分别称为1和-1。那么可以得到约束条件
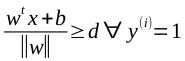
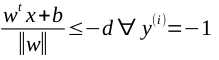
因为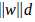
是常数所有化简得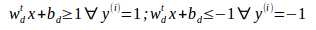
为方便表达写为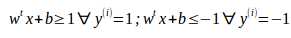
，注意此
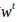非彼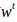
进一步化简得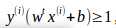
由于支持向量到边界的距离就是1,所有最大化问题转换为min||w||,为方便后面的计算改写成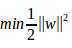
最终我们得到一个带约束条件的优化问题
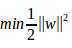
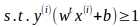
那么如何求解带约束条件的优化问题呢？
这里我们应用拉格朗日对偶性，由对偶问题求原问题。
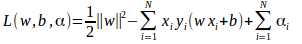
解对偶问题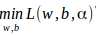
求偏导：
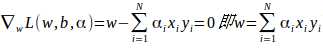
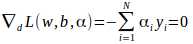
代入得：
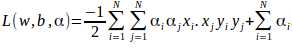
由数值计算得到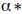
再由对偶问题的解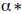
得到原问题的解：
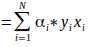
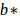
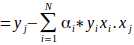
至此，我们得到了在线性可分的情况下决策边界的表达式。
但是在实际生活中很多情况是线性不可分的，如何解决非线性问题呢？这里我们引入升维的概念。
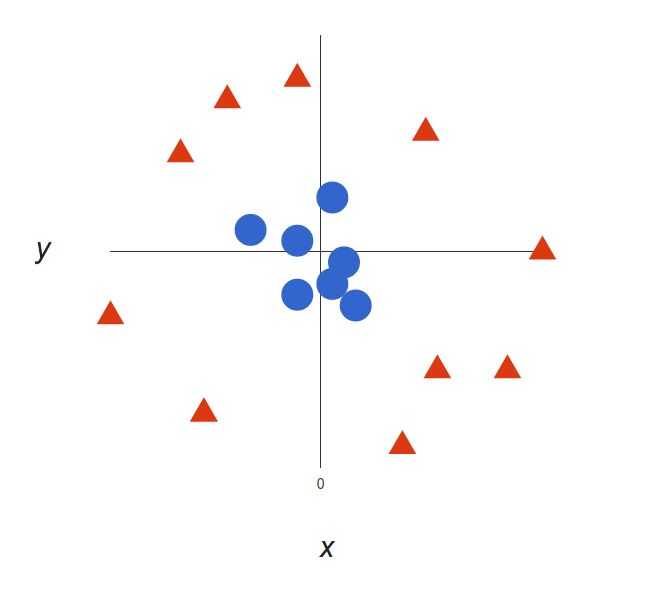
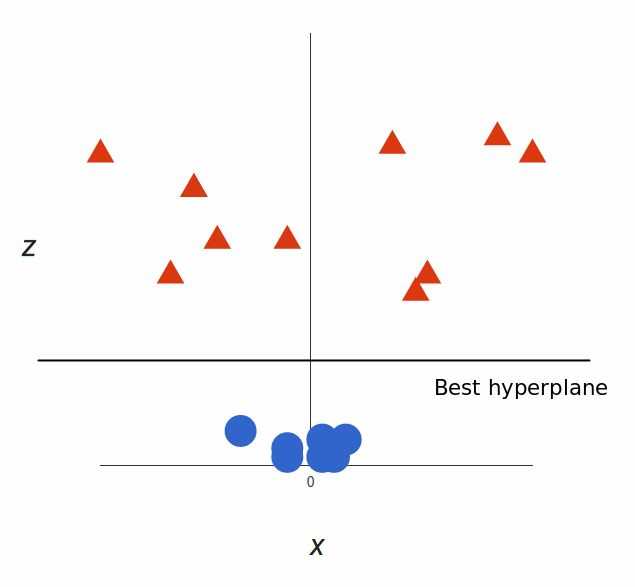
很明显，上图中我们无法找出一个线性决策边界。这个时候我们需要引入第三个维度，即z = x2 + y2
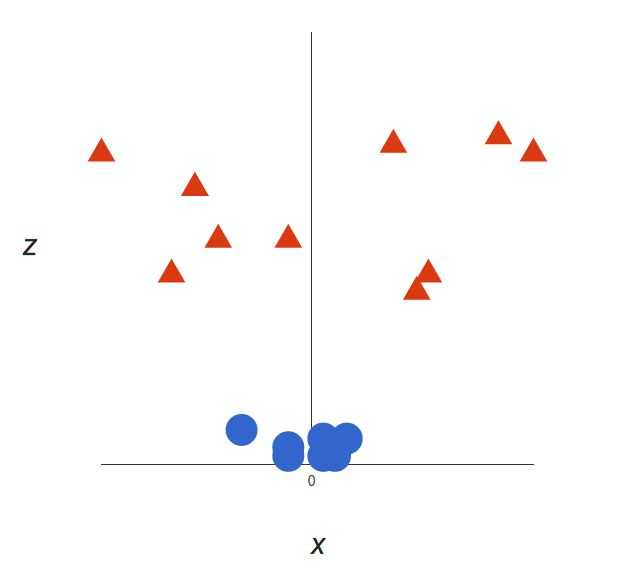
这样我们就能用一条直线来做边界了
然而这种映射到高维度的方法会极大的增加计算量。为了减少工作量我们引入核函数的技巧。
核函数是二元函数，输入是变换之前的两个向量，其输出与两个向量变换之后的内积相等。这样的“巧合”让我们可以忽略了映射而通过核函数直接计算映射后的值。
也就是说将问题转换为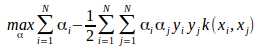
我们就不用在高维空间计算了。
一般用到的核函数如下：
线性核函数：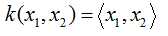
多项式核函数：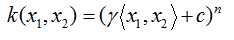
径像基核函数/高斯核函数：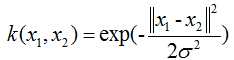
拉普拉斯核函数：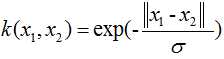
sigmod核函数：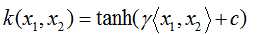
至于如何选择核函数，一般来说，线性情况就用线性核，非线性的时候用径像基核就可以了。
结语：
这是渣本的学习心得，如有错误欢迎大家指正：）
彩图来源：https://monkeylearn.com/blog/introduction-to-support-vector-machines-svm/
标签：uri 泛化 错误 如何 决策 学习心得 class 提高 machine
原文地址：https://www.cnblogs.com/zhabendejqxx/p/8969478.html
