标签:ref nbsp 证明 情况下 tar href 图片 png style
ZJOI结束了,感觉该做点数学题提神醒脑。于是挑了几道奥赛经典上比较简单的几题划划水~~
转载请注明链接 http://www.cnblogs.com/Blog-of-Eden/p/8971594.html,谢谢~
1、一个数集的和是指它的所有元素的和,令S是一些不超过15的正整数组成的集合,
S的任意两个不相交的子集合的和不相等,并且在所有具有上述性质的集合中,S的和最大。
求集合S的和。
(第二章·习题B·1)
先证明集合大小不超过5,然后构造即可。答案:61
2、n是一个正整数,A是集合{1,2,...,n}的子集的一个集合,使得A内无元素包含A的其他元素。
求A的全部元素的个数的最大值。
(第二章·习题B·3)
我的大致想法是,对于A内子集,如果最小的大小为k,且k<[n/2],
我们把所有包含这些子集的大小为k+1的子集去替换这些大小为k的子集,这样A依然合法,并且容易证明元素个数不会减少。
(大致证明:S1为大小为k的子集的集合,设S2为大小为k+1的子集的包含这些子集的集合。
S1内任意元素对应S2中(n-k)个元素,S2中任意元素最多对应S1中(k+1)个元素。
因为n-k>=k+1,又因为对应关系是互相的,所以S2元素个数>=S1元素个数)
对于A内子集,如果最大的大小为k,且k>[n/2],
我们把所有被这些子集包含的大小为k-1的子集去替换这些大小为k的子集,这样A依然合法,同理容易证明元素个数不会减少。
于是,当A内子集大小都为[n/2]时,A的全部元素个数最大。
此时元素个数为C(n,[n/2])。
题解做法比较有趣,对于1到n的全排列,种数为n!个。设A中有fk个k元子集作为元素。|A|=f1+f2+...+fn
当fk>0,对于fk个k元子集中任意一个子集{a1,a2,...,ak},取出前k个元素恰好构成子集{a1,a2,...,ak}的全排列,共有k!(n-k)!个。
由于A中两两元素不包含。因此对于A中所有元素用上述方法取出的全排列必然两两不同。
所以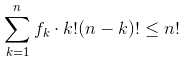 ,
,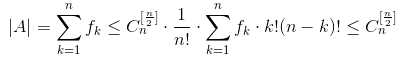
当A取{1,2,...,n}中全部[n/2]元子集组成的集合时,恰达到|A|=C(n,[n/2])
3、n是不小于3的正整数,f(n)表示不是n的因数的最小正整数(例如f(12)=5)。
如果f(n)≥3,又可作f(f(n)),类似的,如果f(f(n))≥3,又可作f[f(f(n))]等等。
如果f(f(···f(n)···))=2 (前面有k次f),就把k叫做n的长度。
如果用Ln表示n的长度,试对任意正整数n(n≥3),求Ln,并证明你的结论。
(第三章·习题B·2)
显然,当n是奇数时Ln=1。
当n为偶数时,设n=2^k * (2m+1) (k是正整数,m是非负整数)
若 1,2,...,2^(k+1)-1 都是n的约数,那么显然f(n)=2^(k+1),Ln=3。
其他情况下,f(n)一定是个奇数,故Ln=2。
4、函数f(x,y)对所有的非负整数x,y满足:
1.f(0,y)=y+1
2.f(x+1,0)=f(x,1)
3.f(x+1,y+1)=f[x,f(x+1,y)]
试确定f(4,1981)
(第三章·习题B·4)
f(0,n)=n+1
f(1,0)=2,f(1,n) = f(0,f(1,n-1)) = f(1,n-1) +1,故 f(1,n)=n+2
f(2,0)=3,f(2,n) = f(1,f(2,n-1)) = f(2,n-1) +2,故 f(2,n)=2n+3
f(3,0)=5,f(3,n) = f(2,f(3,n-1)) = 2*f(3,n-1)+3,故 f(3,n) = 2^n *8-3
f(4,0)=13,f(4,n) = f(3,f(4,n-1)) = 2^f(4,n-1) *8 - 3。设g(n) = f(4,n)+3,g(n) = 2^g(n-1)
则又g(0) = 2^2^2,g(1981) = 2^2^2^2...^2(1983次^2,一共1984个2)
f(4,1984) = 2^2^2^2...^2(1983次^2,一共1984个2)- 3
(留坑待填)
标签:ref nbsp 证明 情况下 tar href 图片 png style
原文地址:https://www.cnblogs.com/Blog-of-Eden/p/8971594.html