最小编辑代价-golang

标签：bubuko   com   分享   表示   src   idt   矩阵   方法   abc   

题目：

给定两个字符串str1和str2，在给定三个整数ic,dc和rc,分别代表插入、删除和替换一个 字符，返回将str1编辑成str2的最小代价。

解题方法：

动态规划。首先生成大小为(M+1)X(N+1)的矩阵dp。

假设str1="av=b12cd3", str2="abcdf"。dp[i][j]表示str1[0:i]编辑成str2[0:j]的最小代价。计算结果如下：

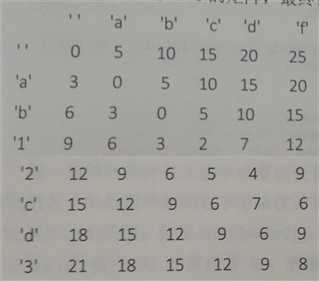
计算步骤：

1、dp[0][0]表示str1空的子串编辑成str2空的子串的代价为0

2、矩阵dp第一列即dp[0:M-1][0], dp[i][0] 表示str1[0:i-1]编辑成空串的最小代价，即把str1[0:i-1]中所有字符删掉的代价，所以dp[i][0] = dc * i

3、矩阵第一行即dp[0][0:N-1], dp[0][j]表示空串编辑成str2[0:j-1]的最小代价，即向空串中添加字符的代价，所以dp[0][j] = ic * j

4、其他位置，从左到右，从上到下计算，dp[i][j]的值可能来自于一下四种情况：

（1）str1[0:i-1]先编辑成str1[0:i-2]，即先删除字符str1[i]，然后由str1[0:i-2]编辑成str2[0:j-1],dp[i-1][j] 表示str1[0:i-2]编辑成石头人[0:j-1]的最小代价，那么dp[i][j]可能等于dc + dp[i-1][j]

（2）str1[0:i-1]可以先编辑成str2[0:j-2],然后向str2[0:j-2]插入字符str2[j-1],编辑成str2[0:j-1]，dp[i][j-1]表示str1[0:i-1]编辑成str2[0:j-2]的最小代价，那么dp[i][[j]可能等于dp[i][j-1] + ic;

  (3) 如果str1[i-1] != str2[j-1], 可以先将str1[0:i-2]编辑成str2[0:j-2],然后将str1[i-1]替换成str2[j-1]，dp[i-1][j-1]表示将str1[0:i-2]编辑成str2[0:j-2]的最小代价，那么dp[i][j]可能等于dp[i-1][j-1]+rc

（4）如果str1[i-1] == str2[j-1], 则此时dp[i][j] = dp[i-1][j-1]

具体代码如下：

func GetDp(str1, str2 []rune, ic, dc, rc int)int{
    rows := len(str1) + 1
    cols := len(str2) + 1
    dp := make([][]int, rows)
    for i, _ := range dp {
        dp[i] = make([]int, cols)
    }
    for i:=0;i < cols;i++{
        dp[0][i] = ic * i
    }
    for i:=0;i < rows;i++{
        dp[i][0] = dc * i
    }
    for i:=1;i<rows;i++{
        for j:=1;j<cols;j++{
            if str1[i-1] == str2[j-1]{
                dp[i][j] = dp[i-1][j-1]
            }else{
                dp[i][j] = dp[i-1][j-1] + rc
            }
            dp[i][j] = getMin(dp[i][j], dp[i][j-1]+ic)
            dp[i][j] = getMin(dp[i][j], dp[i-1][j] + dc)
        }
    }
    return dp[rows-1][cols-1]
}

最小编辑代价-golang

标签：bubuko   com   分享   表示   src   idt   矩阵   方法   abc   

原文地址：https://www.cnblogs.com/youhongpp/p/8973668.html