2.数据挖掘概述——《数据挖掘与数据化运营实战》

标签：其他   线性回归   ash   tno   相互   epg   频繁模式   ati   ada   

2.1 数据挖掘概念

         数据挖掘（Data Mining）是知识发现（KDD）的核心部分，它指的是从数据集合众自动抽取隐藏在数据中的那些有用信息的非平凡过程，这些信息的表现形式为规则、概念、规律及模式等。总体来说，数据挖掘融合了数据库、人工智能、机器学习、统计学、高性能计算、模式识别、神经网络、数据可视化、信息检索和空间数据分析等多个领域的理论和技术。

 2.2 统计分析与数据挖据的主要区别

相对于传统的统计分析技术，数据挖掘有如下特点：

• 数据挖掘擅长处理大数据，尤其是几百万行甚至更大的数据。
• 数据挖掘在实践应用中会借助数据挖掘工具，这些挖掘工具很多并不需要特别专业的统计背景作为必要条件。
• 数据挖掘工具的应用更符合企业实战的需要。
• 从操作者看，数据挖掘技术更多的是企业数据分析师在使用，而不是统计学家用于检测。

数据挖掘与统计分析在如下几方面有显著差异：

• 对数据统计分析时，常常需要对数据分析和变量关系做假设，确定用什么概率函数描述变量关系，以及如何检验参数的统计显著性；在数据挖掘应用中，不需要岁数据分布做任何假设，数据挖掘算法会自动寻找变量关系。
• 统计分析在预测中的应用常表现为一组函数关系式，而数据挖掘在预测应用中的重点在于预测的结果，很多时候并不会从结果中产生明确的函数关系式。

2.3 数据挖掘的主要成熟技术

2.3.1 决策数（Decision Tree）

在决策树里，所分析的数据样本先是集成为一个树根，然后经过层层分支，最终形成若干个结点，每个结点代表一个结论。

决策树的构造不需要任何领域的知识，最大的优点在于所产生的一系列从树根到树枝的规则，可以很容易地被分析师理解，而且这些典型的规则甚至不用整理，就是现成的可以应用的业务优化策略。另外，决策树技术对数据分布甚至确实非常宽容，不容易受到极值的影响。

目前，最常用的决策树算法是CHAID,CART,ID3：

• CHAID(Chi-square Automatic Interaction Detector)：卡方自动相互关系检测。依据局部最优原则，即结点之间互不相关，一个结点确定了后，下面的生长过程完全在结点内进行；利用卡方检验来选择对因变量最有影响的自变量，应用前提是因变量为类别型变量；若自变量存在数据缺失情况，则把确实数值作为单独的一类数值。
• CART(Classification and Regression Tree)：分类与回归树。着眼于总体优化，即先让树尽可能地生长，然后再回过头对树进行修剪；采用的标准不是卡方检验，而是基尼系数等不纯度的指标；CART所产生的决策树是二分的，每个结点只能分出两支，并且在树的生长过程中，同一个自变量可以反复多次使用；若自变量存在数据缺失情况，则会寻找一个替代数据填充缺失值。
• ID3(Iterative Dichotomiser)：迭代的二分器。最大特点在于自变量的挑选标准是，基于信息增益的度量选择具有最高信息增益的属性作为结点的分裂属性，其结果就是对分割后的结点进行分类所需要的信息量最小，这也是一种划分纯度的思想；但是信息增益度有个缺点，就是倾向于选择具有大量值的属性，容易使得划分没有任何实际意义。对此，后来发展的C4.5采用信息增益率（Gain Ratio）代替ID3中的信息增益度量，增加了一个分裂信息（SplitInformation）对其进行规范化约束。

决策树技术在数据化运营中的用途体现在：作为分类、预测问题的典型支持技术，它在用户划分、行为预测、规则梳理等方面应用广泛，甚至可以作为其他建模技术前期进行变量筛选的一种方法。

2.3.2 神经网络（Neural Network）

神经网络就是通过输入多个非线性模型以及不同模型中间的加权互联，最终得到一个输出模型。目前主流的“神经网络”算法是反馈传播（Backpropagation），该算法在多层前向型神经网络上进行学习，而多层前向型神经网络又是由一个输入层、一个或多个隐蔽层以及一个输出层组成的，如下图：

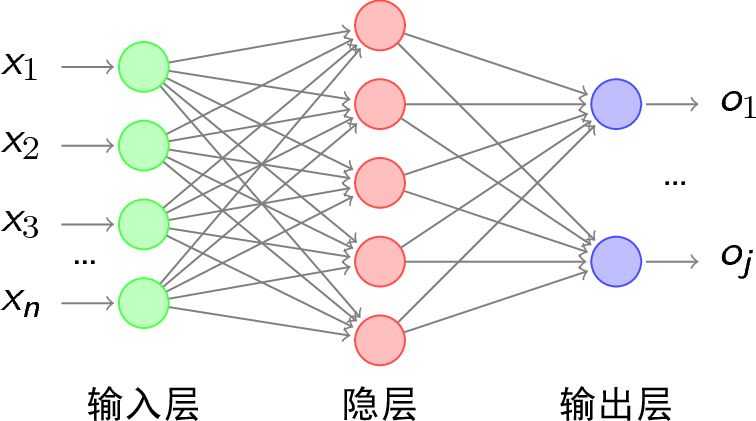
由于神经网络拥有大规模并行结构和信息的并行处理等特点，因此它具有良好的自适应型、自组织性和高容错性，并且具有较强的学习、记忆和识别功能。主要缺点就是其知识和结果的不可解释性，没有人知道隐蔽层里的非线性函数到底是如何处理自变量的，但是这个缺点不影响其应用。

在神经网络技术建模过程中，有以下5个因素对模型结果有着重大影响：

• 层数
• 每层中输入变量的数量
• 联系的种类
• 联系的程度
• 转换函数（也称激活函数或挤压函数）

神经网络技术在数据化运营中主要用途体现在：作为分类、预测问题的重要技术支持，在用户划分、行为预测、营销响应等方面应用广泛。

2.3.3 回归（Regression）

 回归一般指多元线性回归和逻辑斯谛回归，在数据化运营中更多使用的是逻辑斯谛回归，它又包括响应预测、分类划分等内容。多元线性回归在统计分析中更为常见，在此不作介绍。

凡是预测“二选一”事件的可能性，都可以采用逻辑斯谛回归方程。其预测的因变量是介于0和1之间的概率，如果对这个概率进行换算，就可以用线性公式描述隐蔽哪里与自变量的关系了，具体公式如下：

逻辑斯谛回归采用最大似然法估计参数，此方法的优点是在大样本数据中参数的估值稳定、偏差小，估值方差小。

2.3.4 关联规则（Association Rule）

关联规则数据挖掘的主要目的是找出数据集中的频繁模式（Frequent Pattern），即多次重复出现的模式和并发关系（Cooccurrence Relationship），即同时出现的关系，频繁并发关系也称作关联。

应用关联规则最经典的案例就是购物篮分析，通过分析顾客购物篮中商品之间的关联，可以挖掘顾客的购物习惯，从而帮助零售商更好地制定有针对性的营销策略。以下举一个简单的例子：

婴儿尿不湿 → 啤酒 [ 支持度=10%，置信度=70% ]

支持度和置信度分别反映规则的有用性和确定性。这个规则表明，有10%的顾客同时购买了婴儿尿不湿和啤酒，而在所有购买了婴儿尿不湿的顾客中，占70%的人同时还购买了啤酒。发现这个关联规则后，就可以把尿不湿和啤酒摆放在一起进行促销，这就是发生在沃尔玛超市中“啤酒与尿不湿”的经典营销案例。

在众多关联规则数据挖掘算法中，最著名的是Apriori算法，该算法具体分为以下两步进行：

（1）生成所有的频繁项目集。一个频繁项目集是一个支持度高于最小支持度阈值（min-sup）的项目集。

（2）从频繁项目集中生成所有的可信关联规则。这里可信管理规则是指置信度大于最小置信度阈值（min-conf）的规则。

关联规则算法不但在数值型数据集的分析中有很大用途，而且在纯文本文档和网页文件中，也有重要用途。比如发现单词之间的并发关系以及web的使用模式等，这些都是数据挖掘、搜索及推荐的基础。

2.3.5 聚类（Clustering）

聚类分析的算法可以分为划分的方法（Partitioning Method）、层次的方法（Hierarchical Method）、基于密度的方法（Density-based Method）、基于网格的方法（Grid-based Method）、基于模型的方法（Model-based Method）等，其中前面两种方法最为常用。具体的聚类方法在大多数统计课本中有介绍，在此不再赘述。

2.3.6 贝叶斯分类方法（Bayesian Classifier）

贝叶斯分类方法主要用来预测类成员间关系的可能性。比如通过一个给定观察值的相关属性来判断其属于一个特定类别的概率。有研究表明，朴素贝叶斯方法甚至可以跟决策时和神经网络算法相媲美。

设X表示n个属性的测量描述；H为某种假设，比如假设某观察值x属于某个特定的类别C；对于分类问题，希望能通过给定的C的测量描述，来得到H成立的概率，计算出改观察知属于类别C的概率。相比于先验概率P(H)，后验概率P(H|X)基于了更多的信息，而P(H)是独立于X的。如果给定数据集里面有M个分类类别，通过朴素贝叶斯分类法，可以预测给定观察知是否属于具有最高后验概率的特定类别，也就是说，朴素贝叶斯方法预测X属于类别C_i时，表示当且仅当：

P(C_I|X)>P(Cj|X)  1≤j≤m  ,  ,j≠i

即最大化 P(C_I|X)，只需最大化P（X|Ci）P(Ci)。

2.3.7 支持向量机（Support Vector Machine）

与传统的神经网络相比，支持向量机不仅结构简单，而且各项技术的性能也明显提升，因此它成为当今机器学习领域中的热点之一。

支持向量机以结构风险最小为原则。在线性的情况下，就在原空间寻找两类样本的最优分类超平面。在非线性情况下，它使用一种非线性的映射，将原训练集数据映射到较高的维上。在新的维上，它偶所线性最佳分离超平面。使用一个适当的足够高维的非线性映射，两类数据总可以被超平面分开。

支持向量机的基本概念如下：

设给定的训练样本集为{（x₁,y₁）,(x₂,y₂),...,(x_n,yn)}，其中x_i属于Rⁿ，y属于{-1,1}

再假设该训练集可被一个超平面线性划分，设该超平面记为（w，x）+ b = 0

支持向量机的基本思想可用下图的两维情况举例说明：

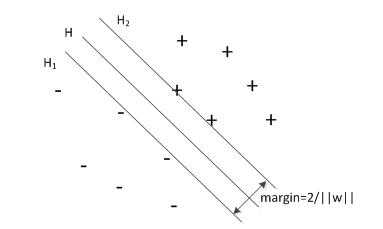
图中的加号和减号代表两类样本，H为分类线，H₁和H₂分别为过各类样本中离分类线最近的样本并且平行于分类线的直线，它们之间的距离叫做分类间隔（Margin）。所谓最优分类线就是要求分类线不但能将两类正确分开（训练错误为0），而且能使分类间隔最大。推广到高维空间，最优分类线就成了最优分类面。

其中距离超平面最近的一类向量被称为支持向量，一组支持向量可以唯一确定一个超平面。通过学习算法，SVM可以自动寻找出那些对分类有较好区分能力的支持向量，由此构造出的分类器则可以最大化类与类的间隔，因而有较好的适应能力和较高的分类准确率。支持向量机的缺点是训练数据较大，但是它的优点也是很明显的——对于复杂的非线性的决策边界的建模能力高度准确，并且也不太容易过拟合。

2.3.8 主成分分析（Principal Components Analysis）

2.3.9 假设检验（Hypothesis Test）

以上两种方法，主成分分析和假设检验，在常见的统计分析书中都有详细论述，在此不再赘述。

2.数据挖掘概述——《数据挖掘与数据化运营实战》

标签：其他   线性回归   ash   tno   相互   epg   频繁模式   ati   ada   

原文地址：https://www.cnblogs.com/data-science-chinchilla/p/8973201.html