标签:font 表示 之间 com 条件 sqrt 特征 ack sch
深度学习出现之前,机器学习方面的开发者通常需要仔细地设计特征、设计算法,且他们在理论上常能够得知这样设计的实际表现如何;
深度学习出现后,开发者常先尝试实验,有时候实验结果常与直觉相矛盾,实验后再找出出现这个结果的原因进行分析。
给定一个网络结构(层数以及每层的神经元个数),根据参数取不同的值形成不同的函数。换句话说,给定了一个网络结构,即定义了一个函数集合。
给定一个目标函数\(f(x)=2(2\cos^2(x)-1)^2-1\),现在想用一个神经网络来拟合这个函数(根据目标函数采集对应的多组\((x,y=f(x))\)对形成训练数据来训练神经网络)。
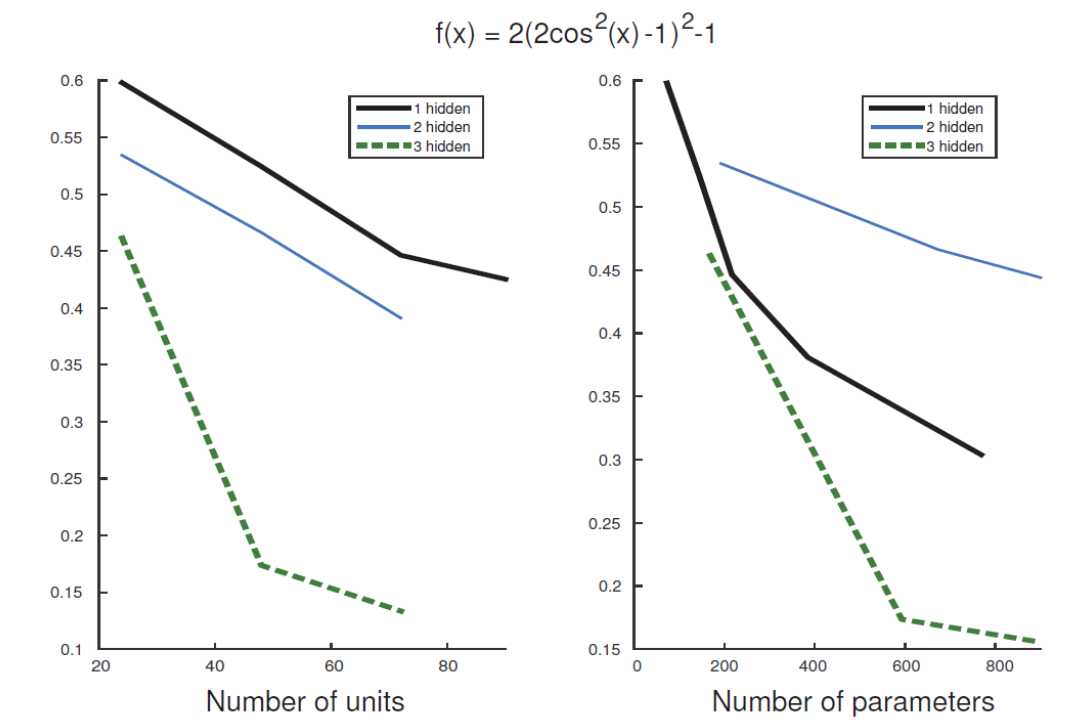
从图0-1中可以看出,随着神经元个数/参数数目(参数数目与神经元个数成正比)的增多,拟合的效果越来越好。
从横向看,达到同样的拟合效果,越深的网络结构需要参数的数目越少;
从纵向看,同样的参数数目下,越深的网络结构达到的拟合效果越好。
接下来假设输入X为标量,且取值属于[0,1],输出Y也为标量,隐藏层激活函数均为ReLU。
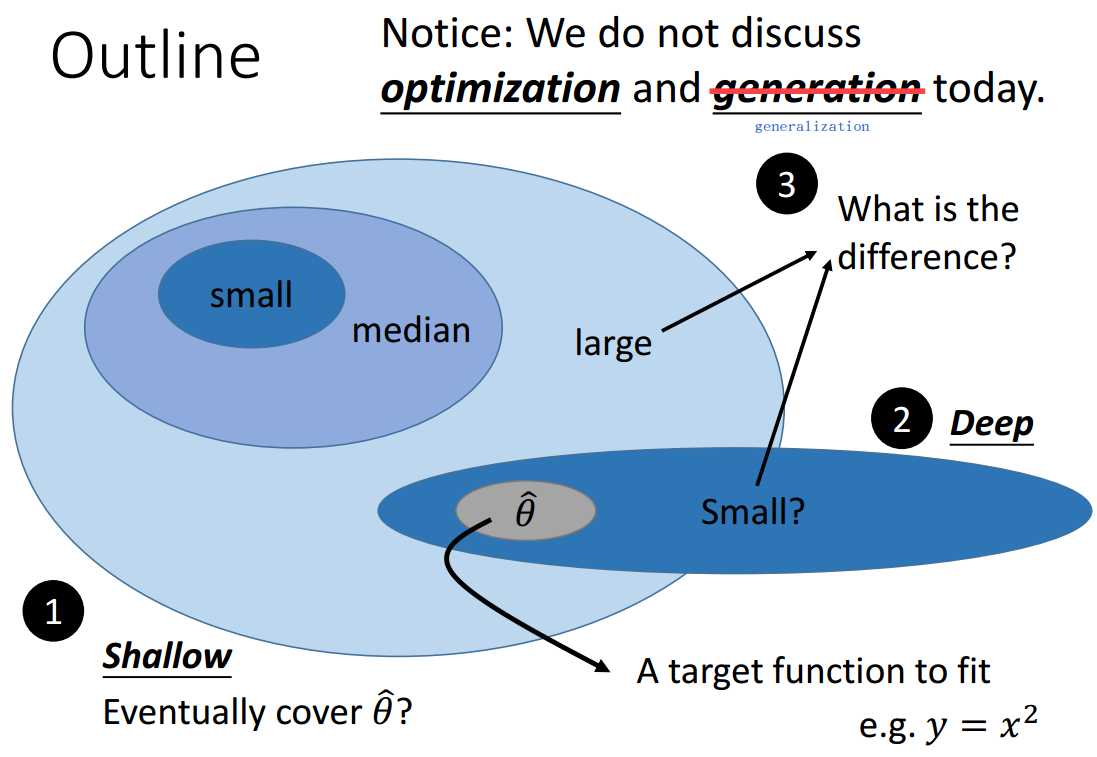
如图0-2所示,接下来只讨论3个主要的问题:1.浅层结构能够拟合任意函数吗?2.为什么需要深层结构呢?3.浅层结构和深层结构的区别是什么?
至于优化问题不讨论,即只要函数集能够覆盖目标函数,我们就假设能够拟合,不管选择的优化方法之间的区别;
至于泛化问题也不讨论,即只考虑基于训练集数据上表现的拟合,不考虑测试集上的表现。
答案是能,只要增加神经元个数,最终一定可以拟合目标函数。
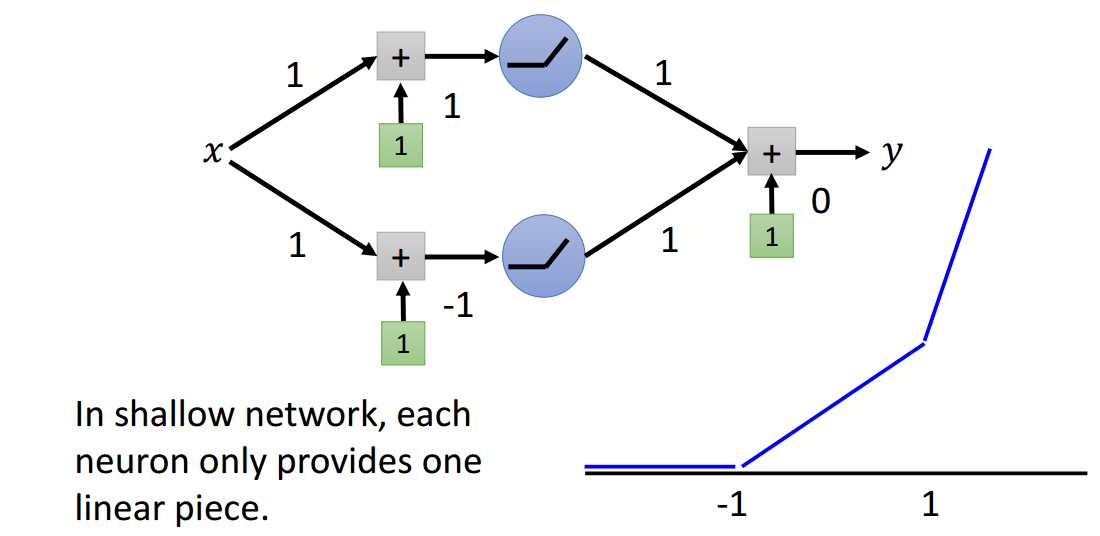
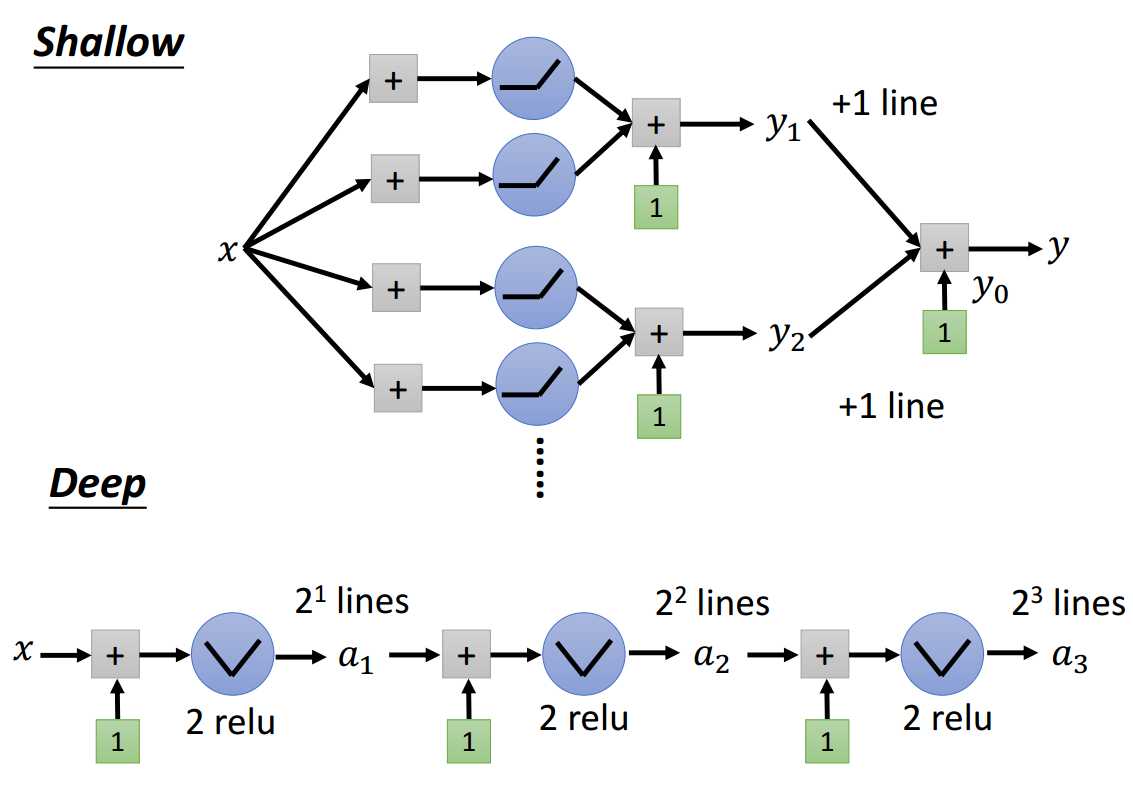
给定一个浅层网络结构(只有一层隐藏层),隐藏层的激活函数为ReLU,以及线性输出层。
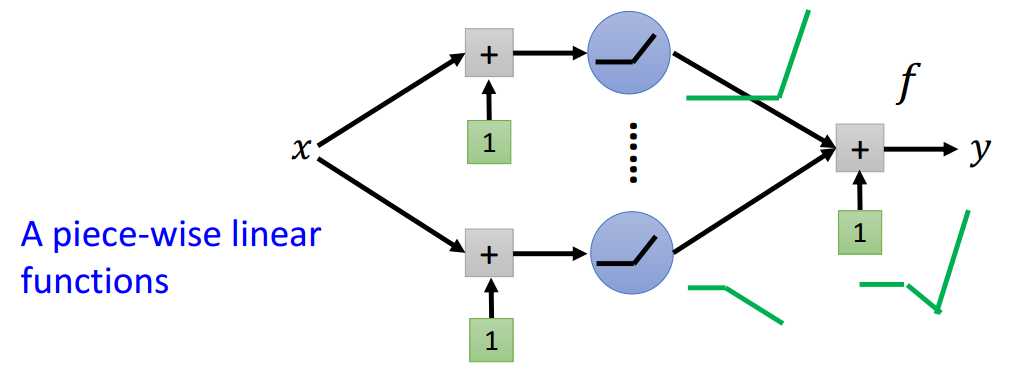
如图1-1所示,很明显,这个浅层网络定义了一个分段线性函数集合。
现给定一个满足L-Lipschitz条件的目标函数\(f^\ast\),需要多少个神经元才能够拟合这个目标函数呢?
什么是L-Lipschitz?
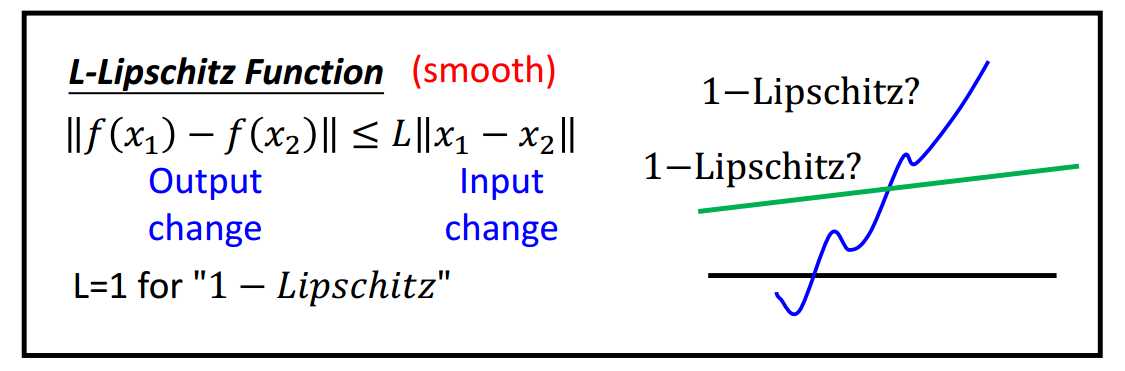
如图1-2所示,即因变量变化的绝对值不超过自变量变化的绝对值的L倍。显然, 图1-2中蓝色线段不满足1-Lipschitz条件。
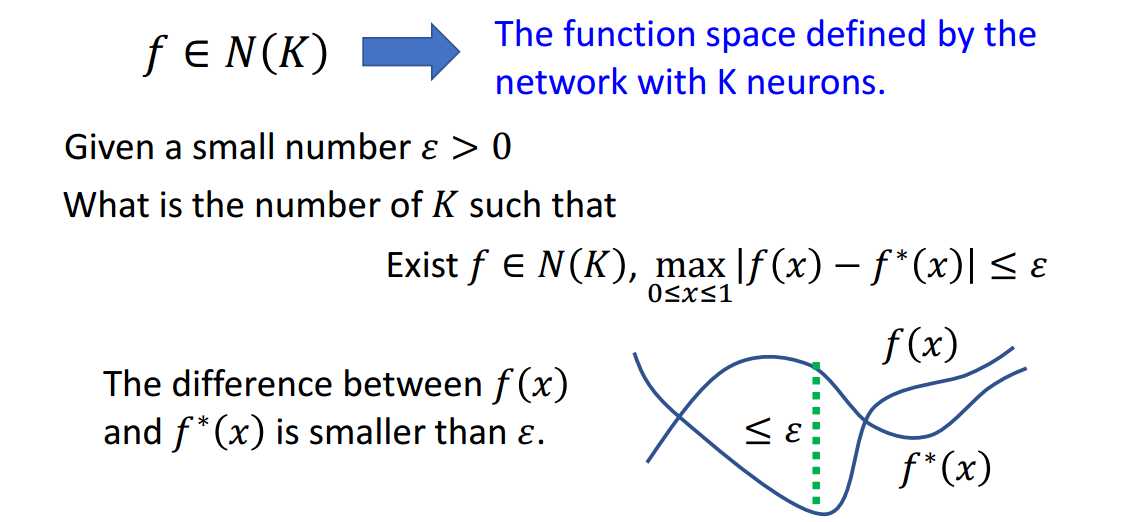
当然,最大误差不超过\(\epsilon\)也可以改为两条曲线在[0,1]间面积不超过\(\epsilon\)。


如图1.1-3所示,满足图1.1-2中蓝色方框里上面的条件的话,下面的条件也会自动被满足。
所以现在的问题是使用\(N(k)\)这个分段线性函数集合中的某个函数\(f\)来拟合目标函数\(f^\ast\),那么\(f\)是如何分段使得最大误差不超过\(\epsilon\)的呢?
假设每段的长度都是\(l\)。
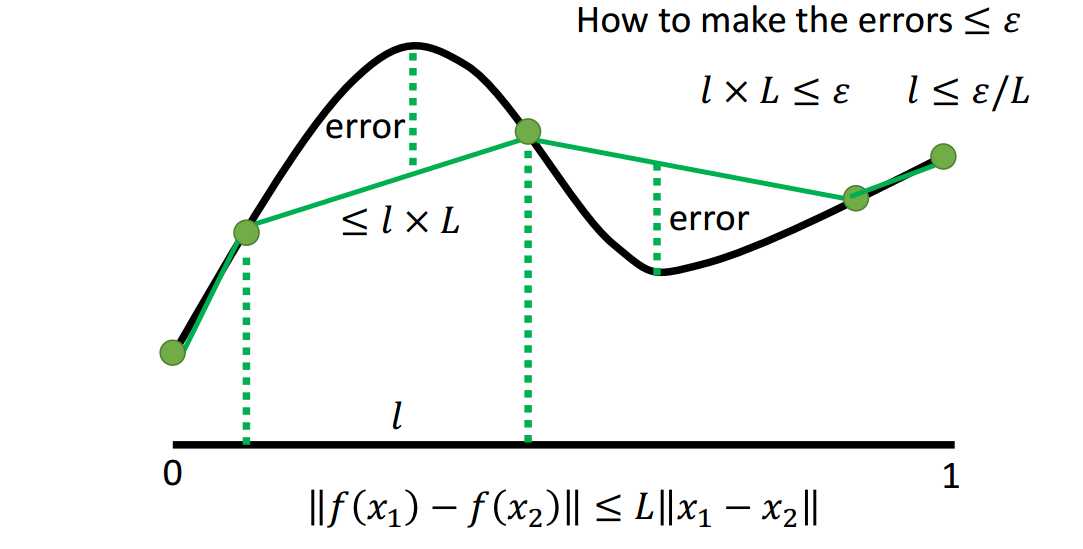
如图1.2-1所示,因为最大误差点和分段点之间的距离是不超过\(l\)的,任意两点间的斜率又是不超过\(L\)的,所以最大误差不超过\(l{\times}L\)。
所以可以通过使得\(l{\times}L\le\epsilon\)来保证最大误差不超过\(\epsilon\),则\(l\le\frac{\epsilon}{L}\),即至少要分\(\frac{L}{\epsilon}\)段。
通过多个神经元结果的叠加。
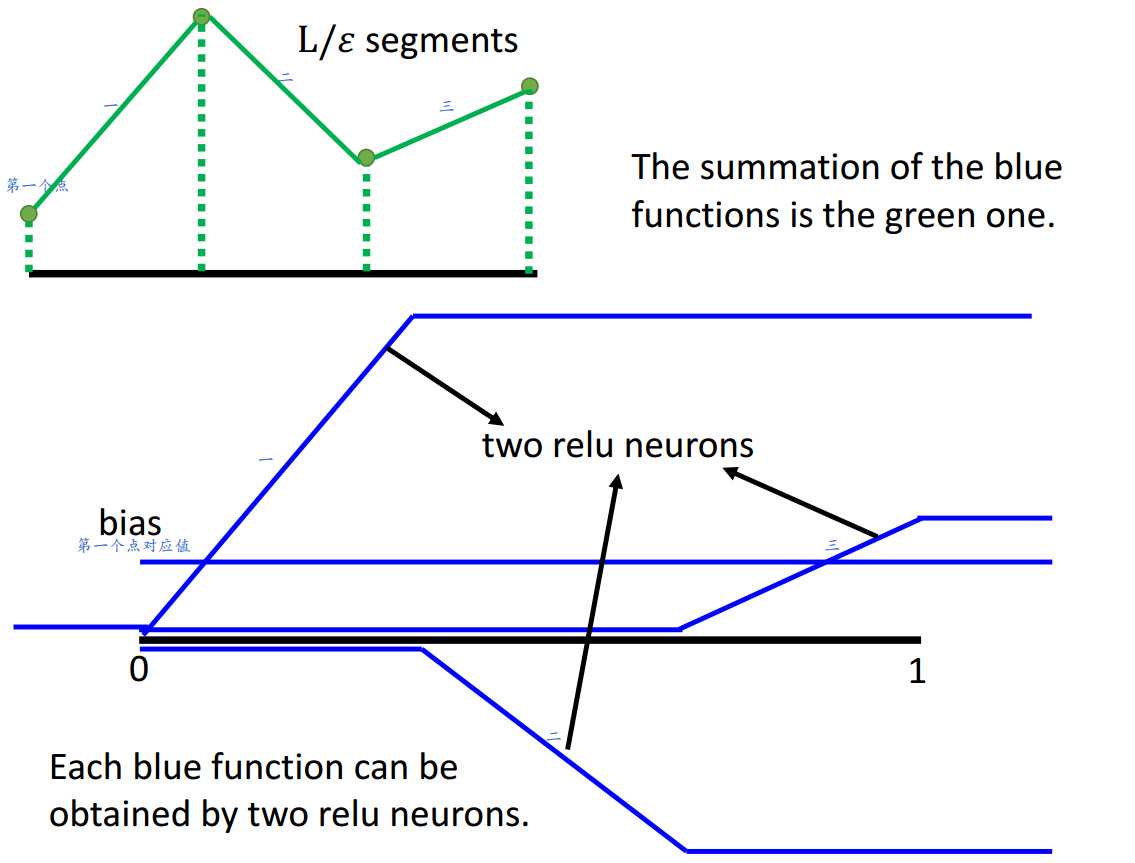
绿线可以由蓝线叠加生成,每条蓝线需要2个神经元结果叠加形成。
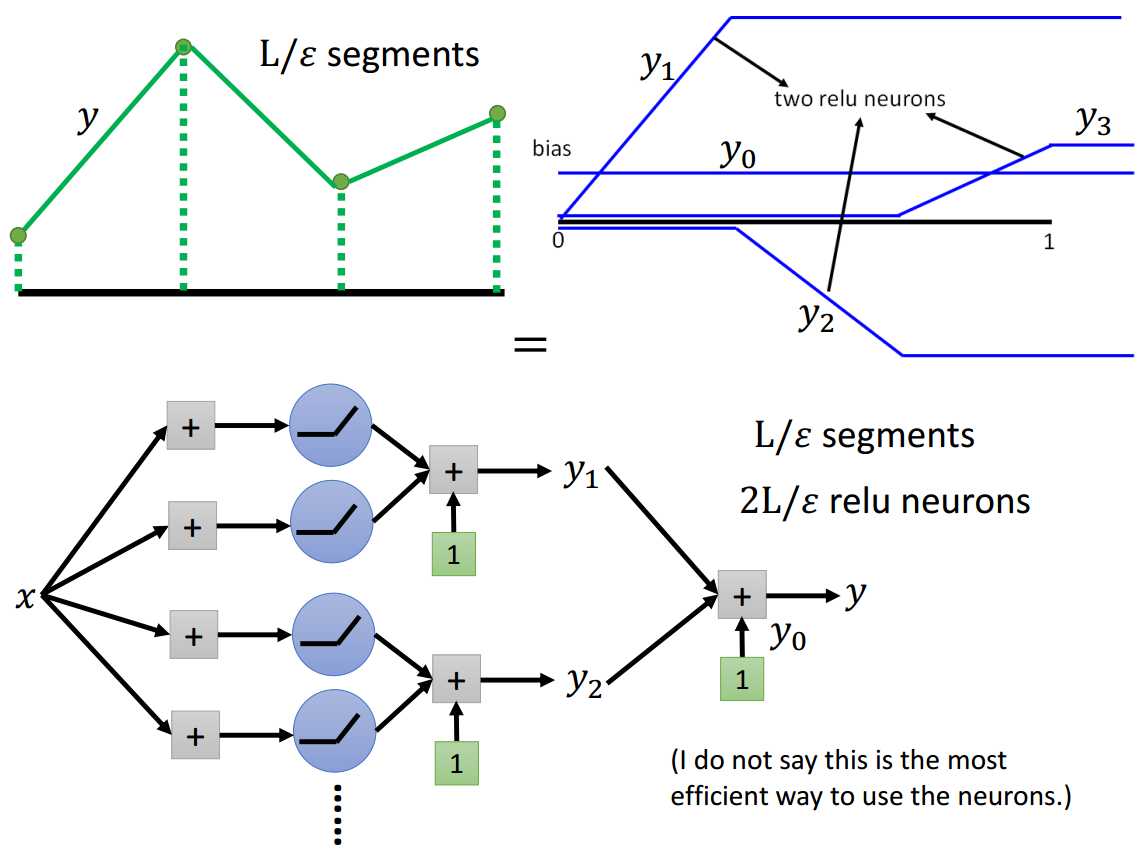
所以,要分成\(\frac{L}{\epsilon}\)段可以通过使用\(\frac{2L}{\epsilon}\)个神经元来实现。
需要注意的是,这里是指需要这么多个神经元可以做到这样的分段方式,并没有指这样子做是最有效率的做法。
当L取任意值时,浅层网络结构可以通过调整神经元个数来拟合对应的目标函数,可见浅层结构可以拟合任意函数,那么为什么需要深层结构呢?
虽然浅层结构可以拟合任何function,但其所需神经元个数可能为\(O(\frac{L}{\epsilon})\),深层结构的使用可以使其变得更有效率。
举例说,任何演算法都可以用2行程式写出来。如排序,穷举所有排序前可能的字符串作为key,其对应的排序结果作为value构建查询表。
程式第1行根据给定输入查表得对应索引,程式第2行输出该索引对应的value值作为最终的结果。------2步对应shallow
但是,在实际实现排序时,我们并不会这样做,会进行更多的其他步骤,为了实现上更有效率。------多步对应deep
上面已经讨论过,ReLU网络(激活函数均为ReLU的网络结构)可以表示分段线性函数。
在差不多数目的参数下,深且窄的ReLU网络比起浅且宽的ReLU网络能实现更多的分段。
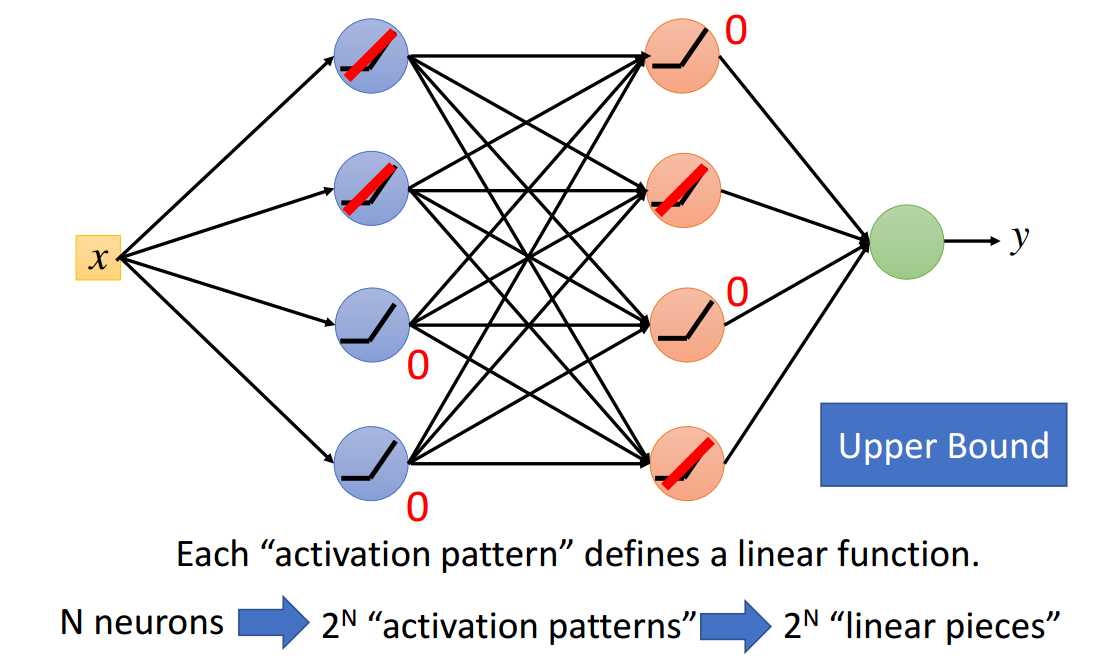
定义神经元个数为\(N\),对应的最大激活模式为\(2^N\)种,每一种激活模式对应一个线性分段,所以最大线性分段数为\(2^N\)个。
但是,不是所有的分段方式都是会出现的。比如图2.1-2中2个神经元,最多只会出现3个分段。
如何定义绝对值激活函数?
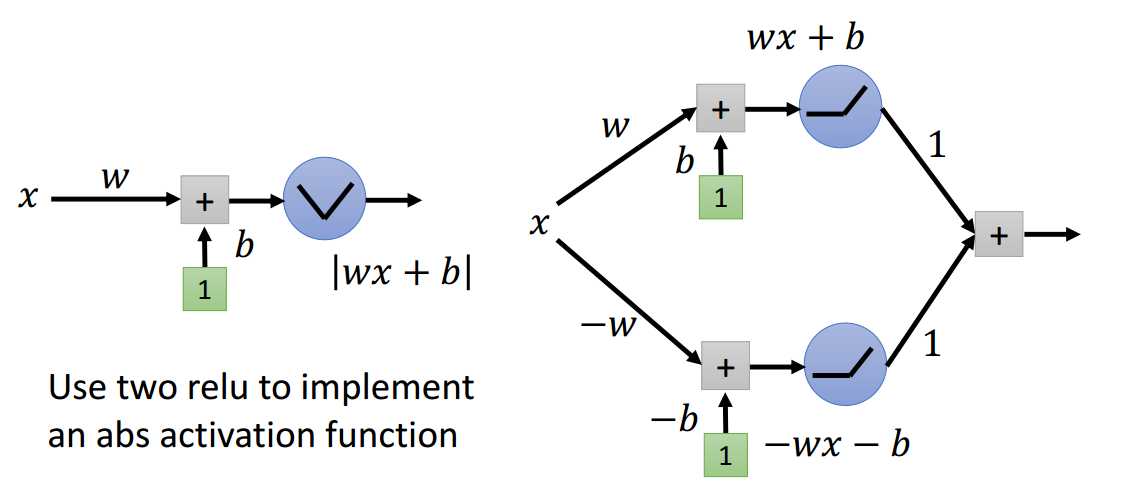
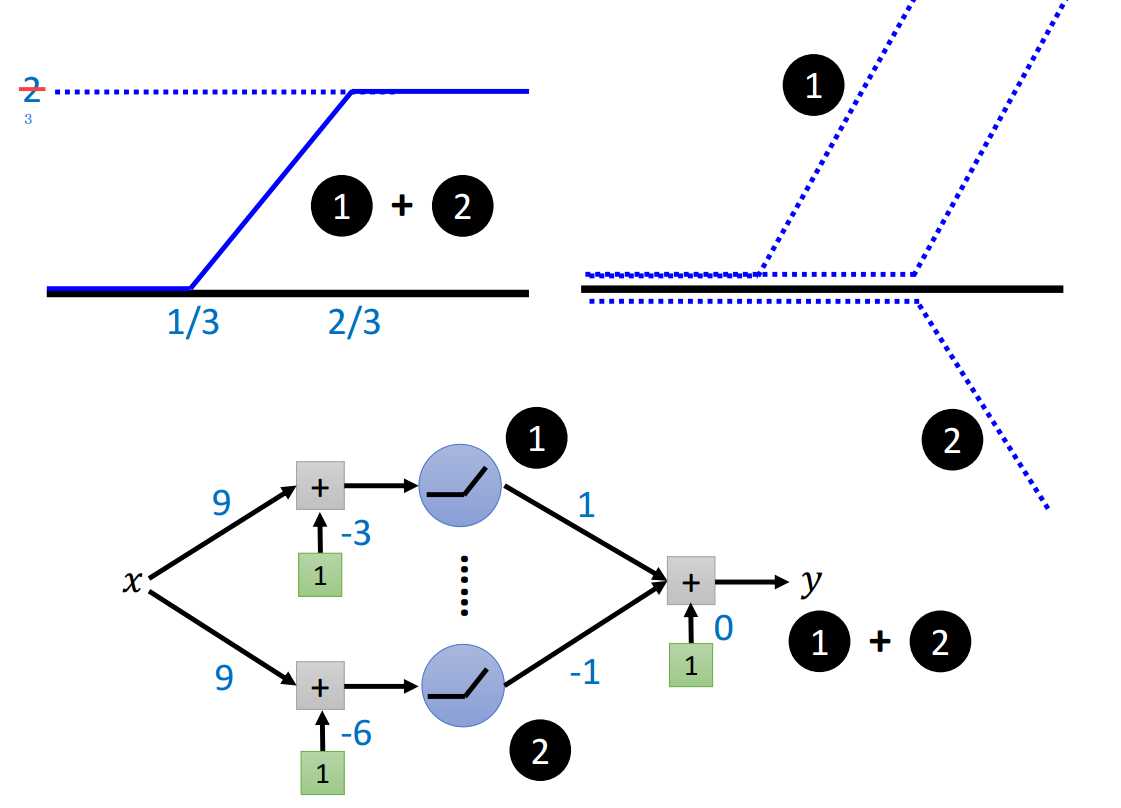
如图2.2-1所示,可以用2个ReLU神经元实现绝对值激活函数功能。
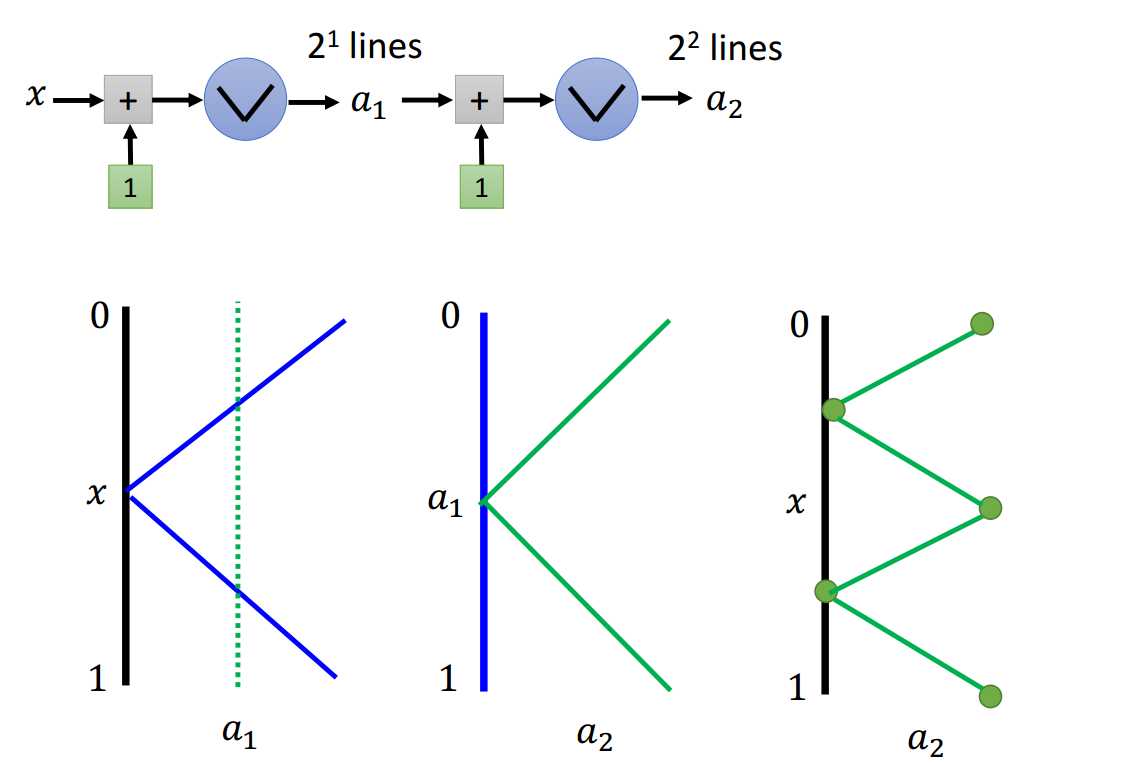
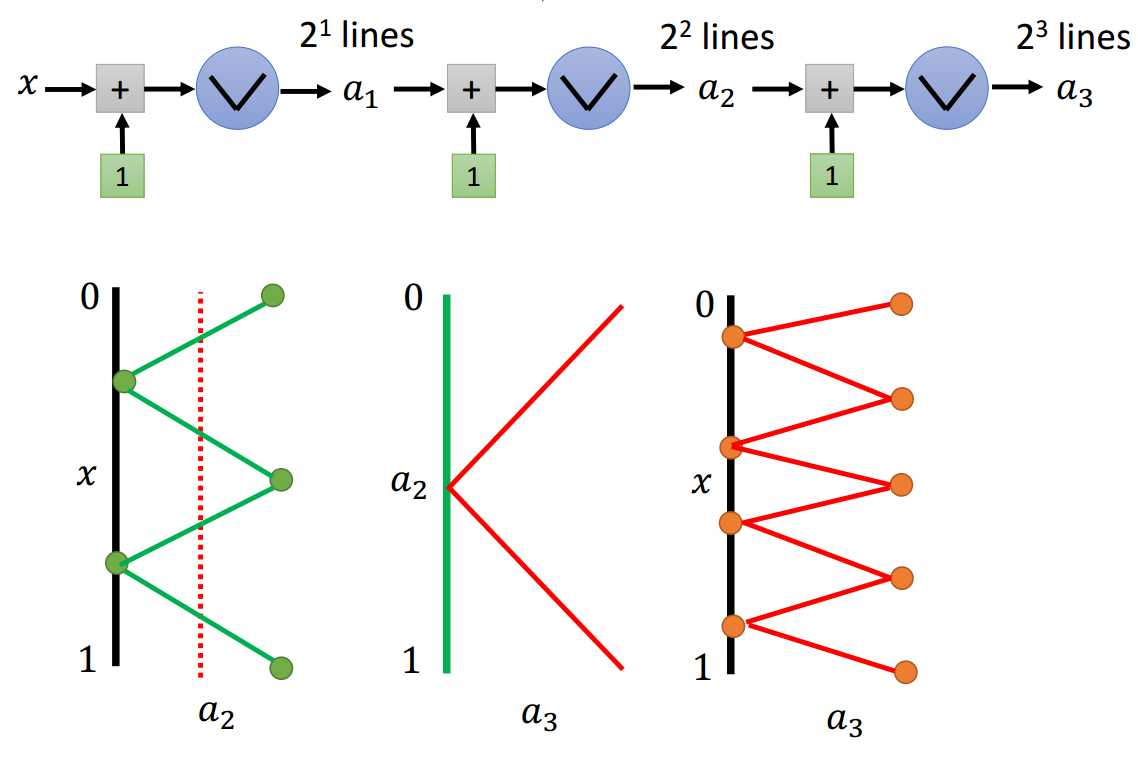
绝对值激活函数进行深度上的堆积,每次多加一个节点,分段数变为原来的2倍。
从图2.2-4中可以看出,对于浅层网络结构,每次多加一个节点(宽度方向上),分段数加1;对于深层网络结构,每次多加一个节点(深度方向上),分段数乘以2。
当网络结构宽度为K、深度为H时,我们至少可以有\(K^H\)个分段数。
可见深度对于分段数的影响要明显高于宽度,因为深度方向的堆积使得同样的pattern可以被反复利用。
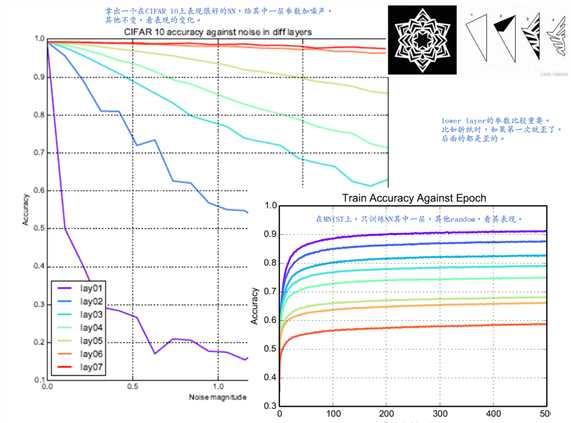
下图的实验结果验证了上述观点,同时显现较低层参数对于网络的表现有更大的影响。
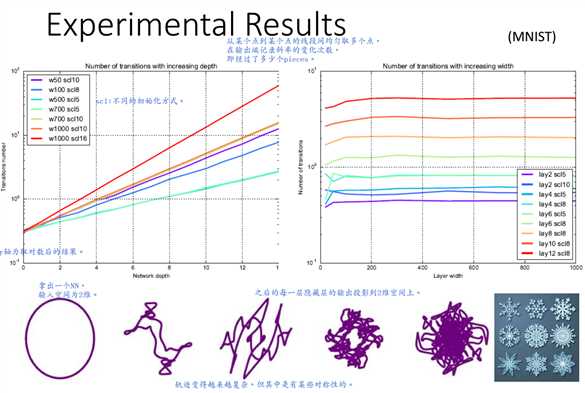
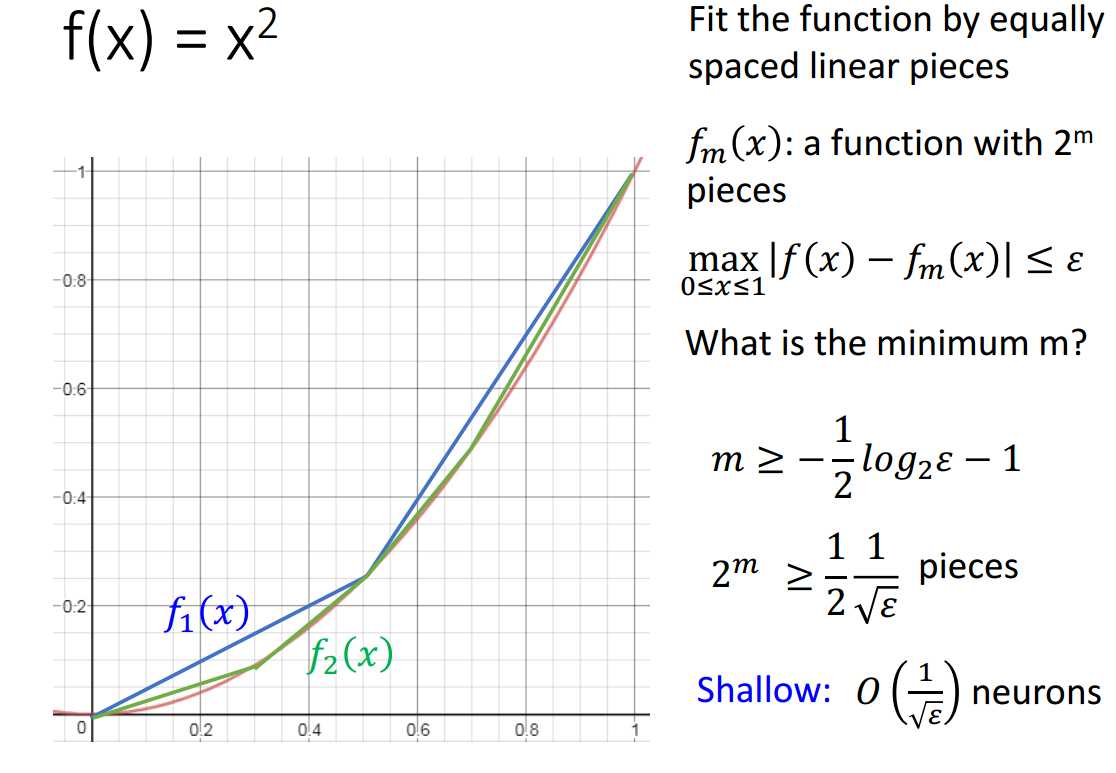

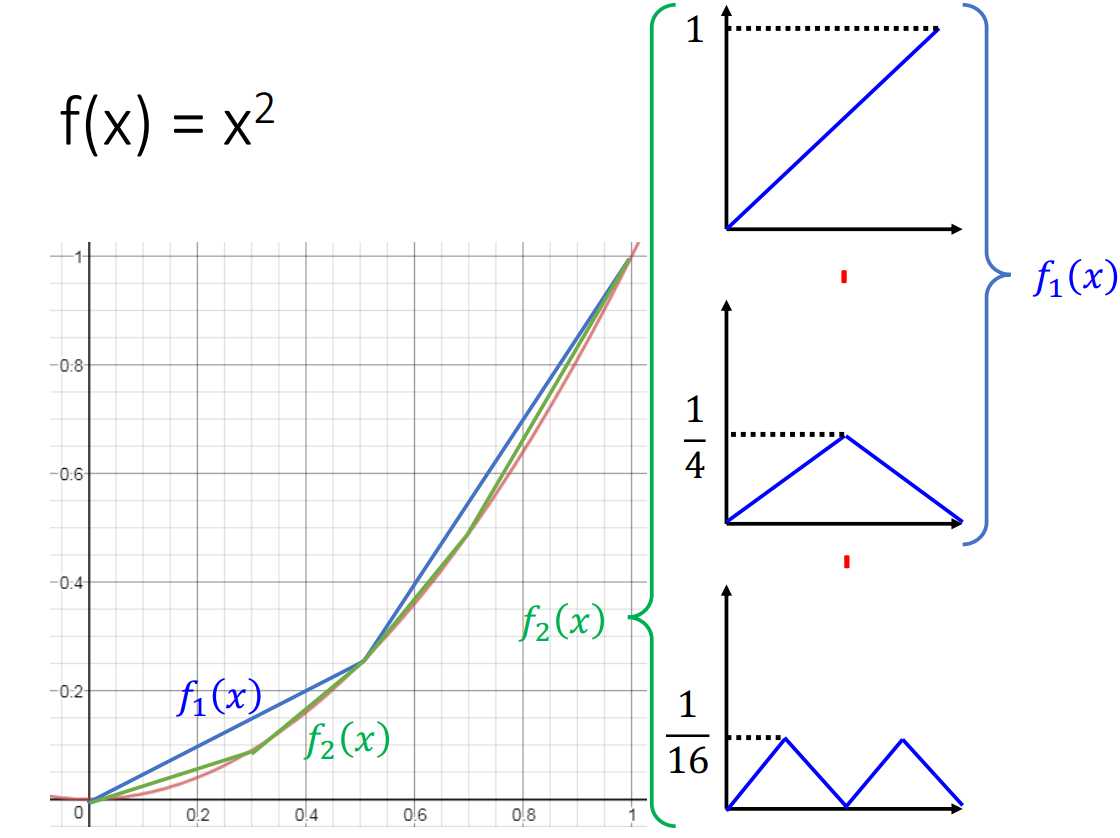
如上图所证,拟合函数\(f(x)=x^2\)时,shallow网络结构所需的神经元个数为\(O(\frac{1}{\sqrt{\epsilon}})\)。
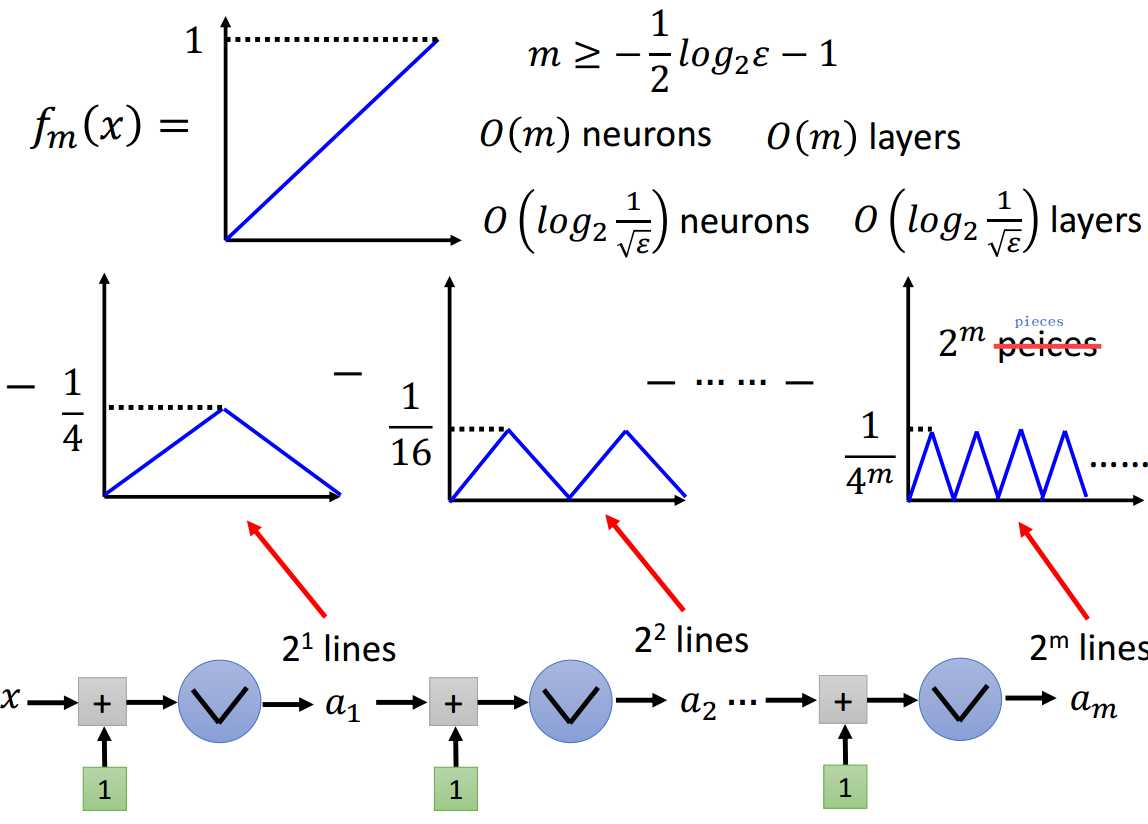
如上图所证,拟合函数\(f(x)=x^2\)时,deep网络结构所需神经元个数为\(O(log_2\frac{1}{\sqrt{\epsilon}})\)。
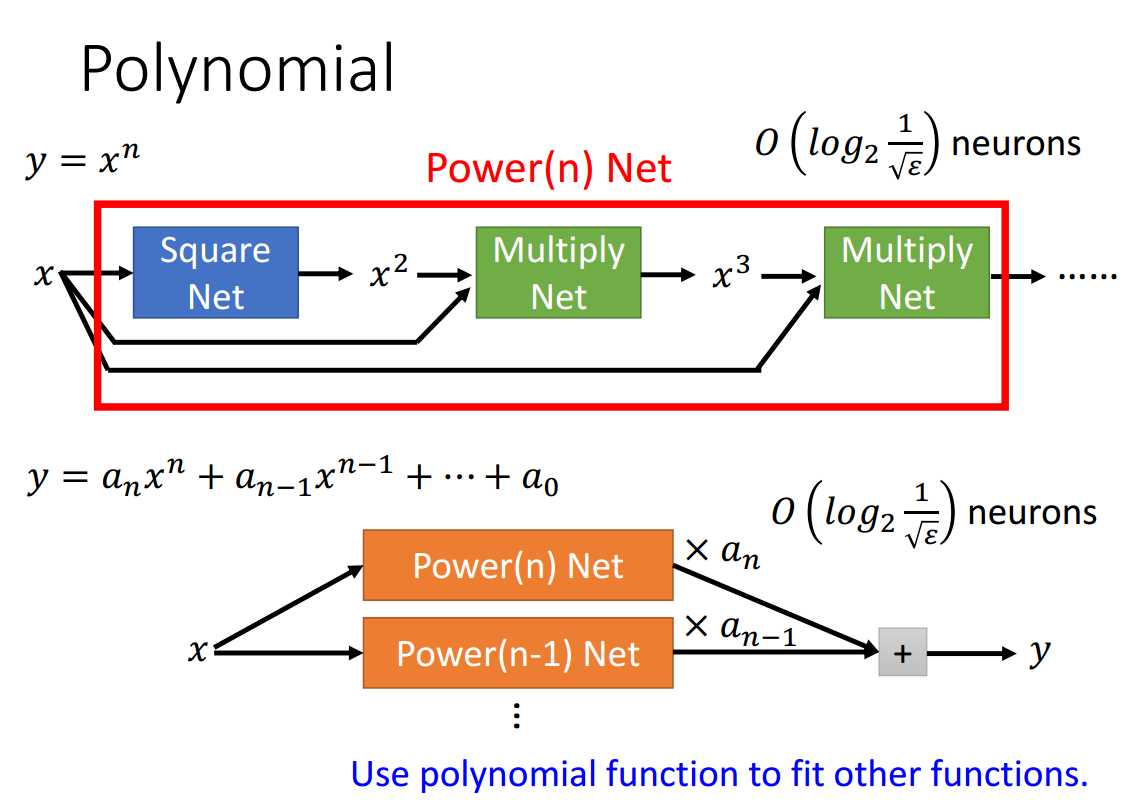
函数\(y=x^2\)是否具有一般性?
具有,因为可以用拟合函数\(y=x^2\)的网络结构作为square net去形成multiply net继而形成polynomial net,就可以用这个多项式网络去拟合其他连续函数了。
目前证明这一点的力量还不足够,因为上述讨论都是基于存在的某种状态,并不清楚这种状态是否是最佳状态。
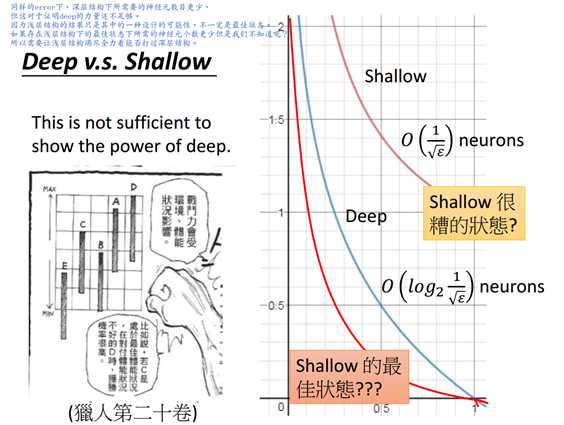
为了求得浅层网络在竭尽全力的状态下拟合函数\(f(x)=x^2\)所需的神经元个数,可以放宽各种条件。
首先,假设相邻黑线之间的头尾无需相接。
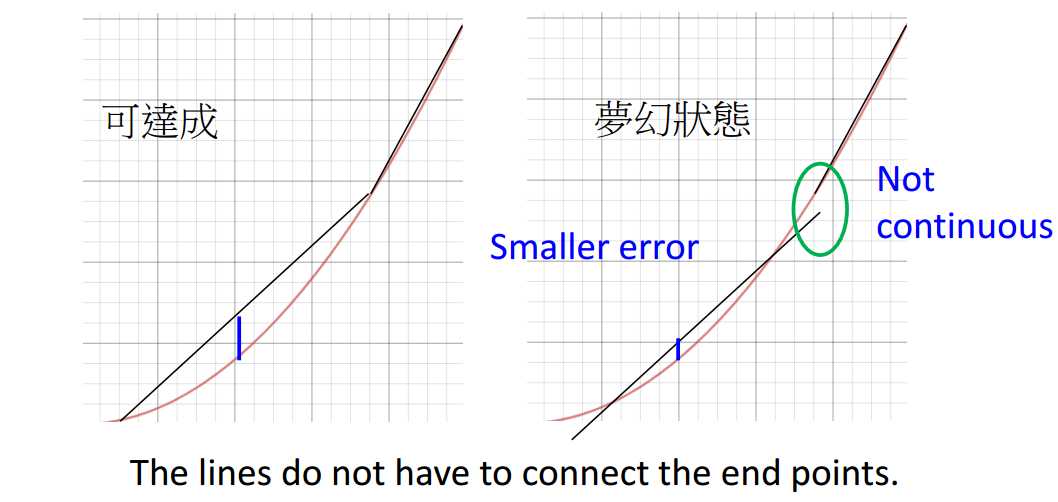
如图3-1所示,左边是可以用ReLU实现的,右边没法通过ReLU实现。因为ReLU无法生成非连续的线。
先假设右边可以实现,因为其对应的error明显更小,称这种状态为梦幻状态。
再来,原来拟合的条件是最大error不超过\(\epsilon\),满足该条件一定满足面积的近似不超过error的条件,但满足后者不一定满足前者。
现放宽限制条件,变为面积的近似不超过error就好。
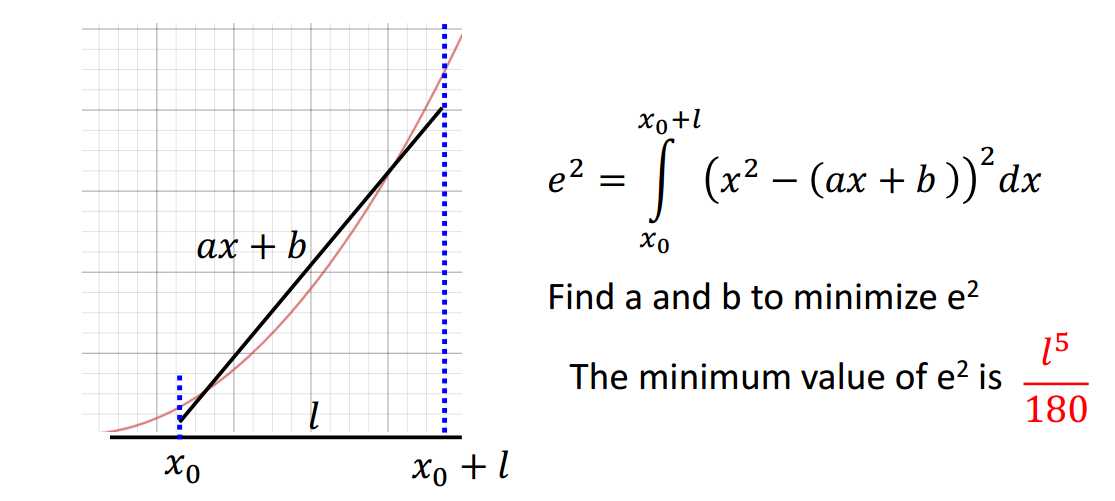
现在考虑给定一个分段,最小的error是多少呢?
答案是\(\frac{l^5}{180}\),证明思路如图3-3所示。
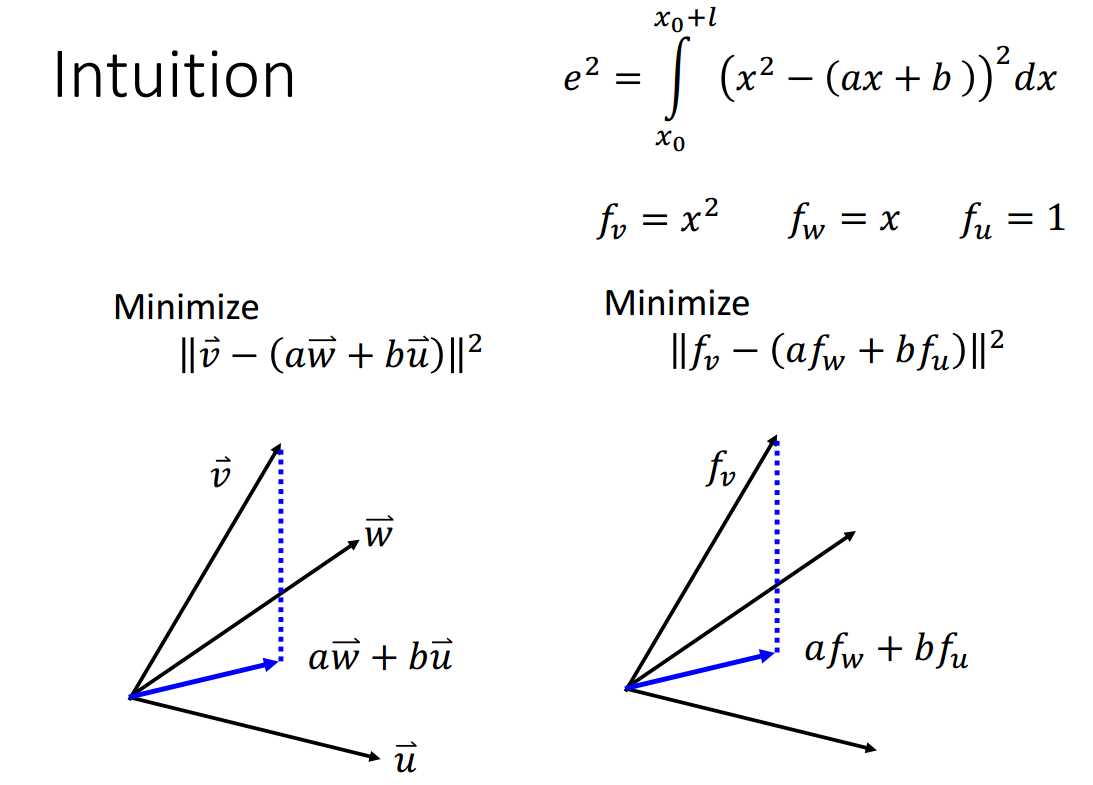
如果分段数确定为n,如何分段使得error最小呢?
直觉是等分n段,证明可以参考图3-5。
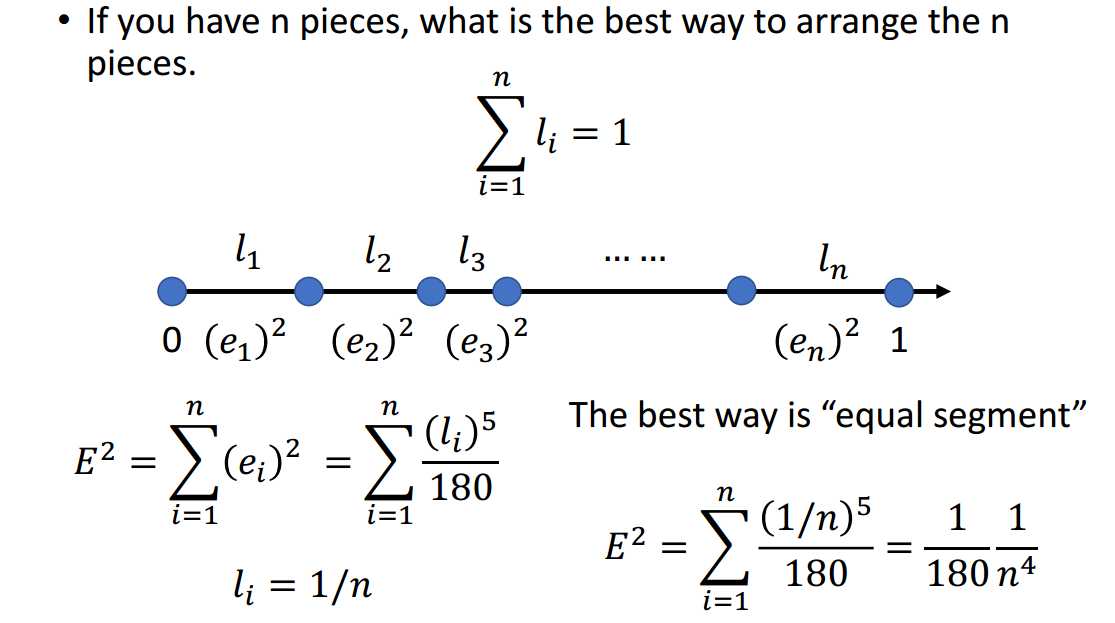

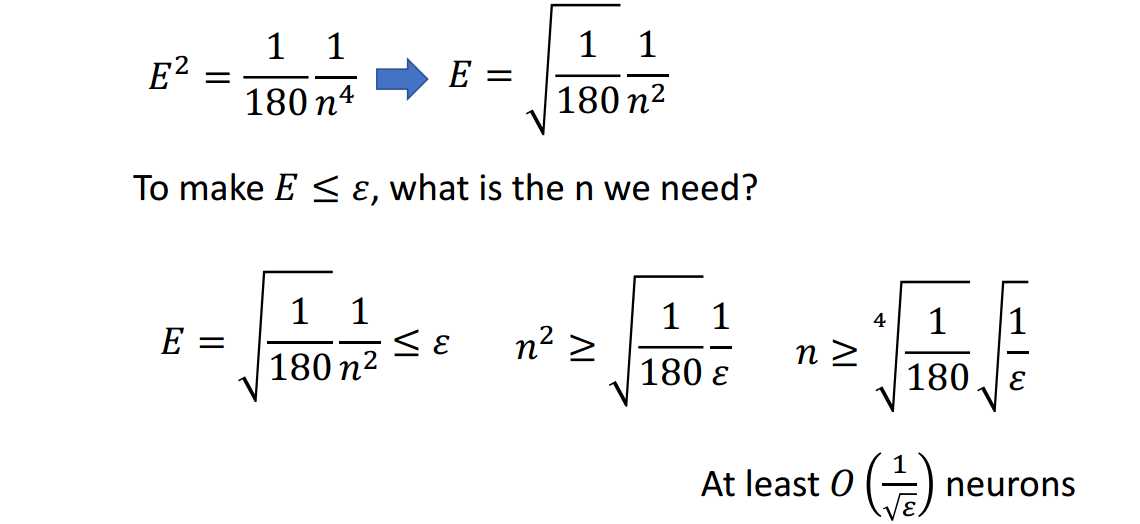
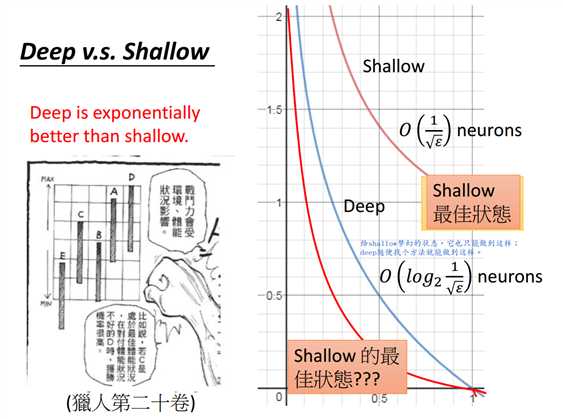
即使浅层网络结构竭尽全力,其所需的神经元个数还是\(O(\frac{1}{\sqrt{\epsilon}})\),而深层网络结构在随意设计的某种状态下所需的神经元个数为\(O(log_2\frac{1}{\sqrt{\epsilon}})\),
可见,深层网络结构确实好于浅层网络结构,且好的程度是指数级的。
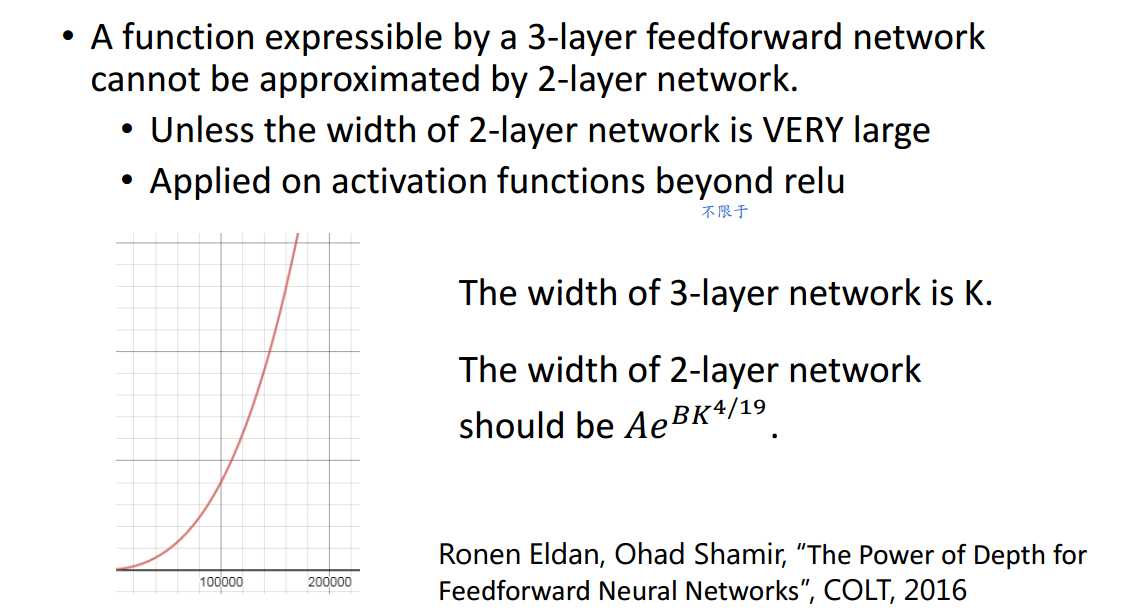

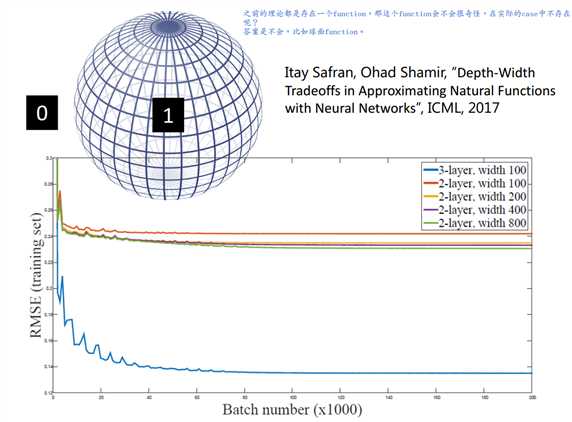

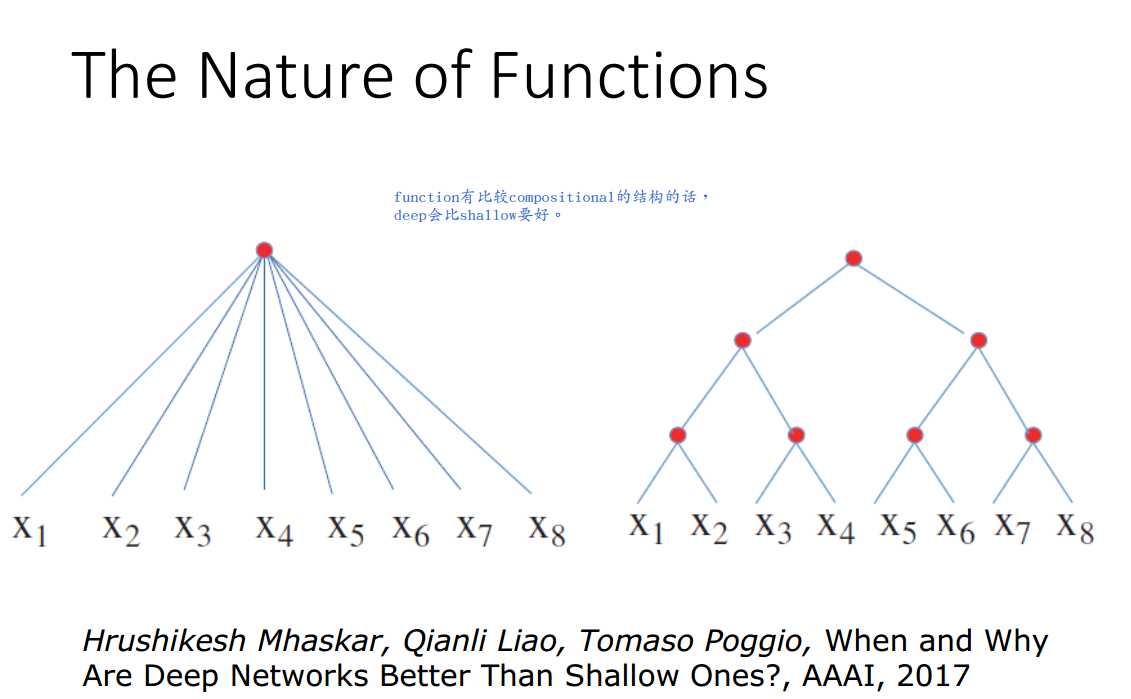
总之,当目标函数满足某种最低复杂度要求时,使用深层网络结构是优于浅层网络结构的,且优于的程度是指数级别的。
因为实际问题中遇到的问题常较为复杂,所以使用深层结构往往更有效。
标签:font 表示 之间 com 条件 sqrt 特征 ack sch
原文地址:https://www.cnblogs.com/cherrychenlee/p/8890175.html