标签:画布 公式 一个 效果 github com 换算 bsp 详细
摘要:Canvas画布是一个二维平面,如何展示出3D效果?通过将三维空间中的Z轴抽取出来,将图像的点投影到与Z轴垂直的平面上,在通过旋转等变换效果,我们就能实现3D效果。
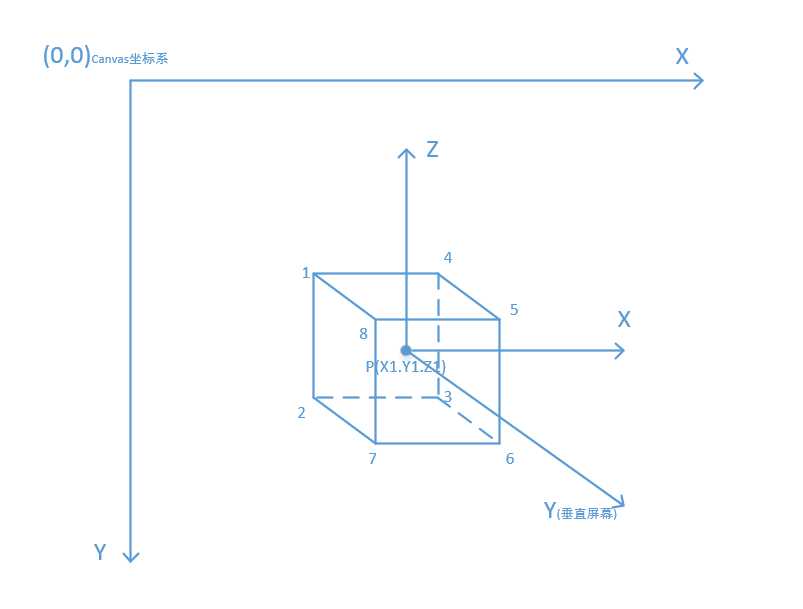
1)立方体坐标系
我们以立方体的几何中心作为原点,如图建立坐标系。
2)canvas坐标系
canvas坐标系主要用于显示3维平面在浏览器中的投影(就像一束光照射在立方体上,在墙面出现的阴影)。三维坐标系的层次在顶层,canvas坐标系在底层。
我们将Y轴抽取出来之后,图像对于屏幕前的我们,主要是围绕Z轴和X轴所处平面的轴在旋转,当我们的鼠标移动时,移动的XY距离可以换算成旋转的角度。立方体在空间中的旋转,我们只需要旋转他的8个顶点,移动后将每个面连起来,就完成了立方体的移动。
PS:这里涉及到了旋转矩阵的知识,不明白的同学可以搜索一下旋转矩阵,有详细的解释,本文不再阐述。
1)绕X轴移动
鼠标向下移动时,我们将移动的距离换算为角度θ,利用旋转矩阵,我们将顶点的矢量与旋转矩阵相乘,即可得到旋转后的点。
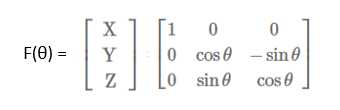
2)绕z轴移动
鼠标向下移动时,我们将移动的距离换算为角度β,继续以上操作。
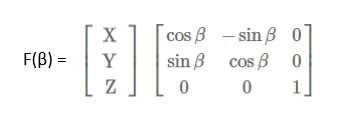
3)XOZ平面上的其他轴
当鼠标斜着移动时,我们可以将其分解为两个方向的移动,在三维空间中也是一样,将图像分解为先绕X轴移动θ角,在绕Y轴移动β角。
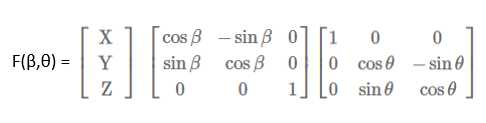
这样我们就可以获得相应的移动公式。
当旋转完毕之后,就需要将旋转后的图像投影到二维平面。直接将Y轴的值去掉,将X轴的值设置为canvas平面的X值,将Z轴的值设置为canvas平面的-Y值。
下载项目后可查看效果,请使用高版本浏览器查看。
https://github.com/sincw/sinwProject/tree/master/webContent/src/main/webapp/work/cube
效果:
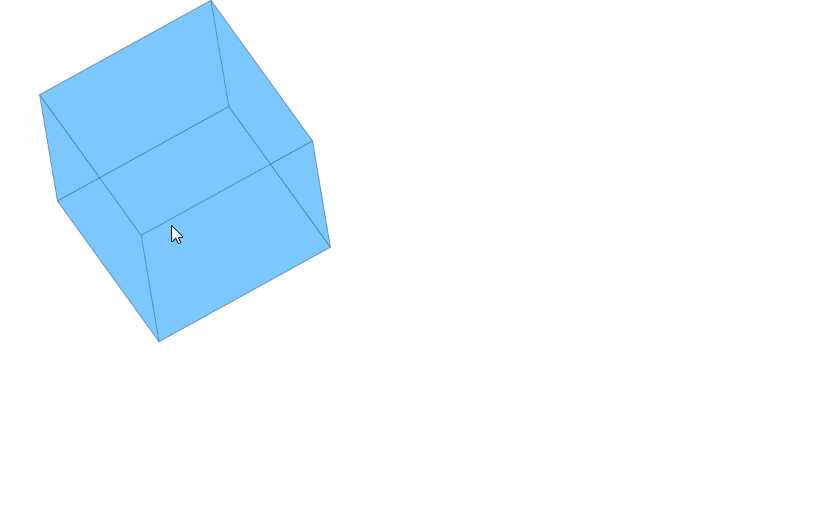
标签:画布 公式 一个 效果 github com 换算 bsp 详细
原文地址:https://www.cnblogs.com/sincw/p/8977157.html