标签:关键点 color oss 为什么 AC 存在 col 结果 神经元
当函数空间覆盖到目标函数时,如何通过优化调整神经网络的参数找到这个目标函数呢?
深度学习中的损失函数是非凸的,非凸优化是个NP-hard问题,如何通过梯度下降来解决这个问题呢?
注意,不同于learning,这里只讨论基于训练集的optimization问题,不考虑在测试集上的表现。
对一个神经网络来说至少存在指数级个数的全局最小值点,因为你将某一层的神经元重新排列后并不改变损失函数值。
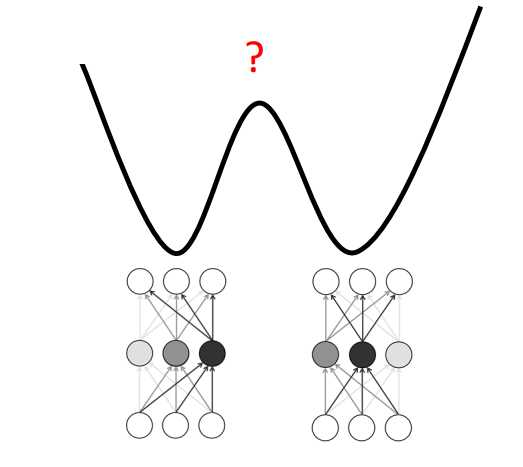
如图0-1所示,线性加权这2组参数所得的loss值不见得变小,说明损失函数是个非凸函数。
但是“非凸”不完全等于“困难”。
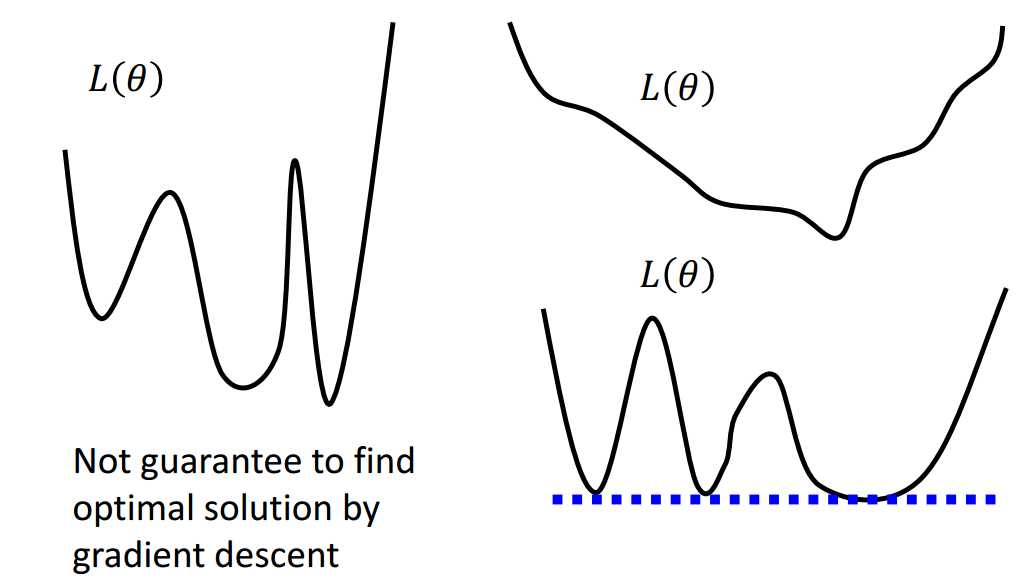
通常来说,非凸函数优化起来很困难,难以用梯度下降找到全局最小值,如图0-2左边所示。
但深度学习中定义的非凸损失函数是否有可能用梯度下降找到全局最小值呢?如图0-2右边所示,有无可能深度学习中定义的非凸损失函数有很多的全局最小值,却没有局部最小值呢?
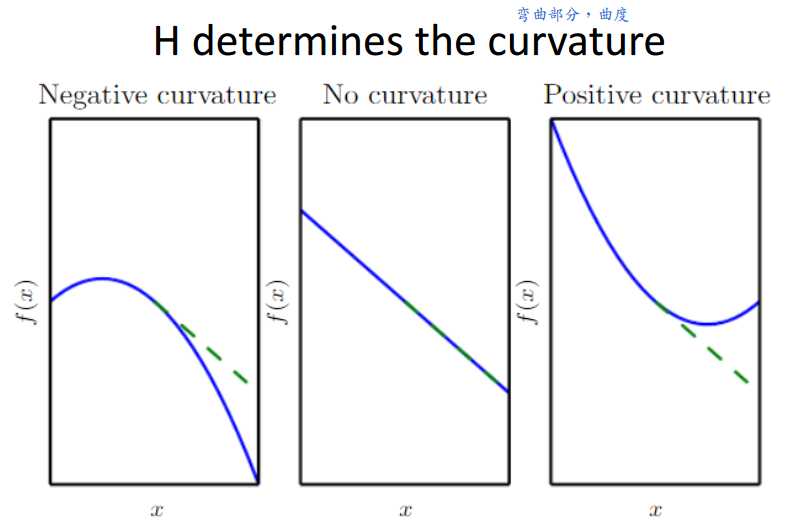
当梯度为0时考虑借助Hessian矩阵进行分析。
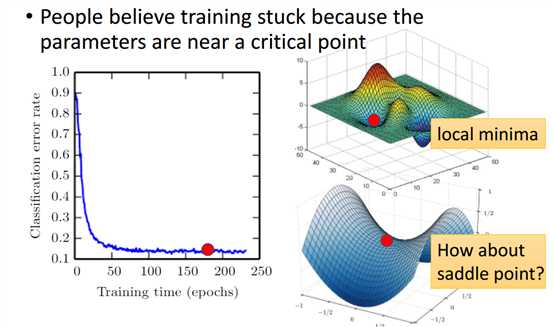
如图1-1所示,人们通常认为训练停止是因为参数到达了关键点,即梯度为0的点。这个点可能是局部最小值点,也可能是鞍点。
什么是Hessian矩阵?
二阶导数值构成的矩阵。
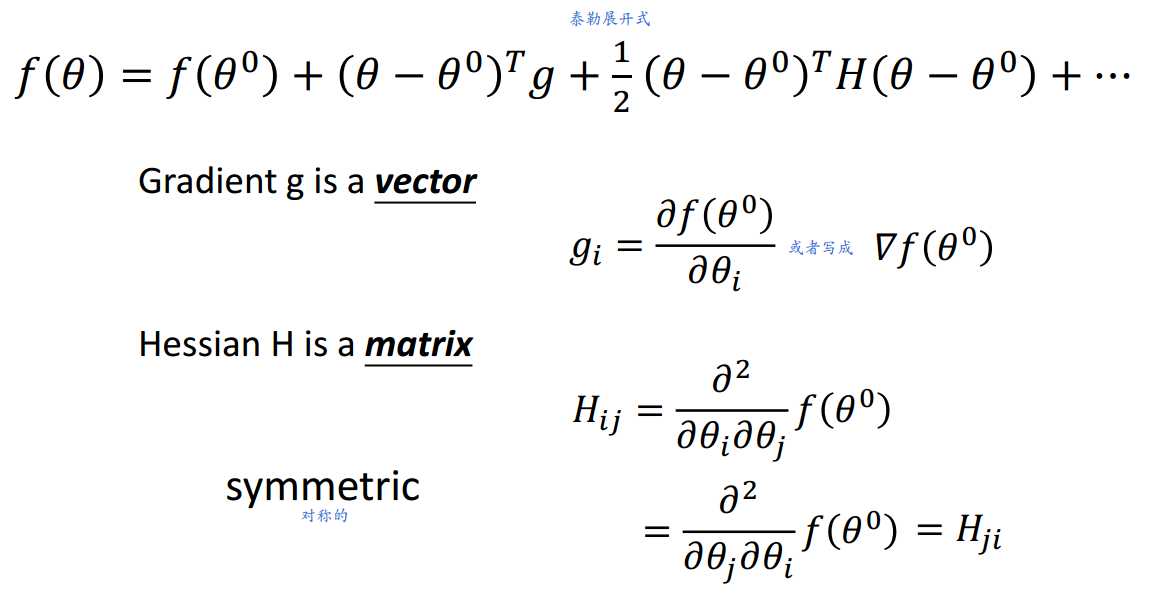

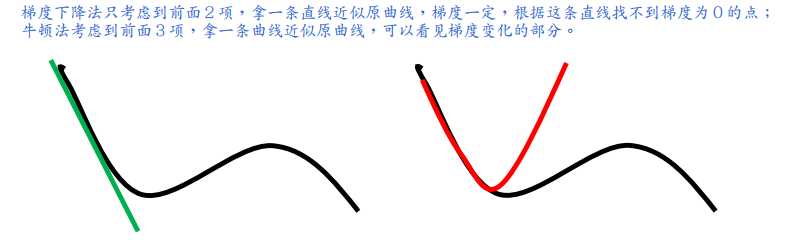
牛顿法是一步到位,梯度下降法是每次走一小步,走许多次。
牛顿法存在的问题:
因此,牛顿法不适合用在深度学习的问题中。
什么是特征值、特征向量?
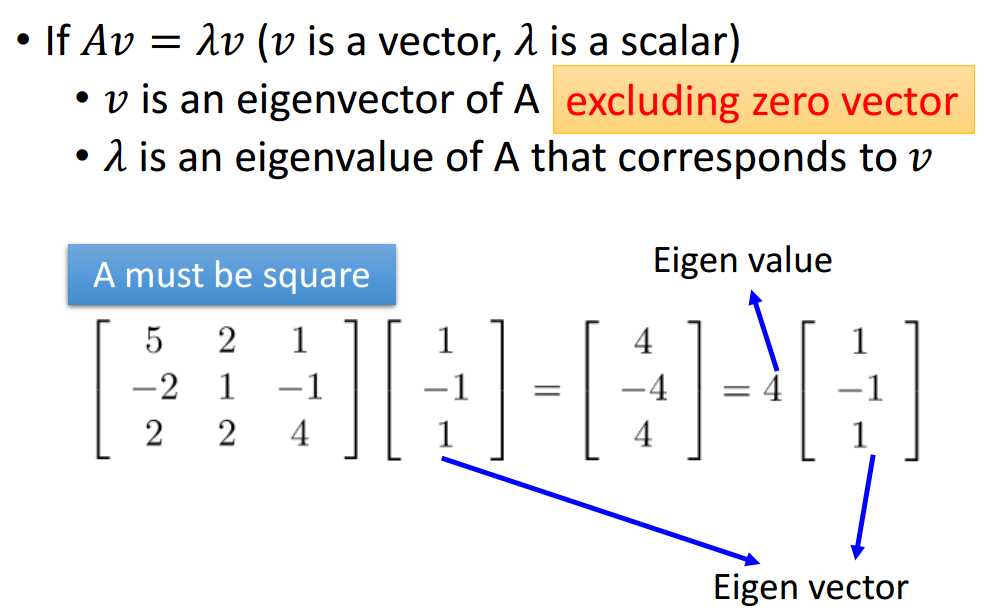
什么是正定、半正定、负定、半负定矩阵?

利用Hessian矩阵帮助区分关键点属性,是局部最小值点,是鞍点,还是局部最大值点?


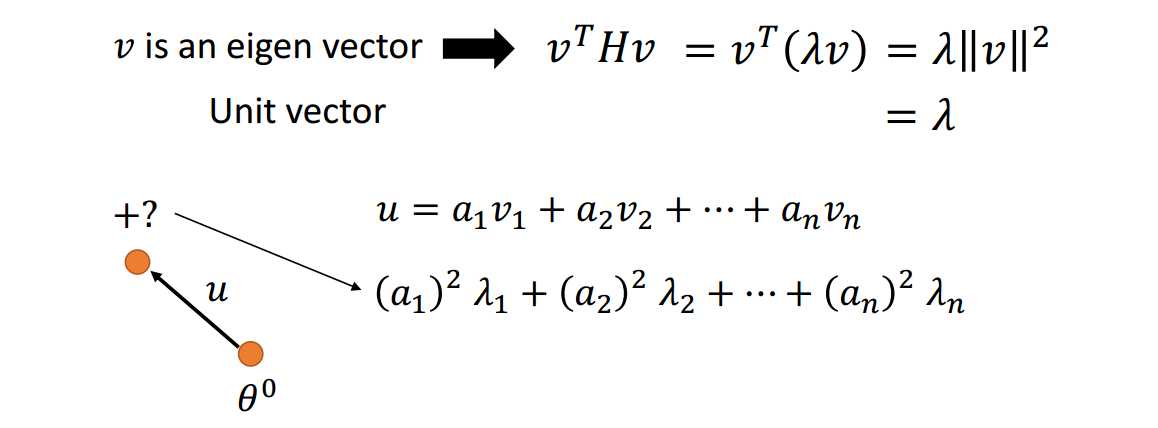
总之,训练停止不一定是到达局部最小值点,可以通过Hessian矩阵进行验证,也可以观察梯度的L2-norm值进行确定。
看看深度线性网络的损失函数surface长什么样子。
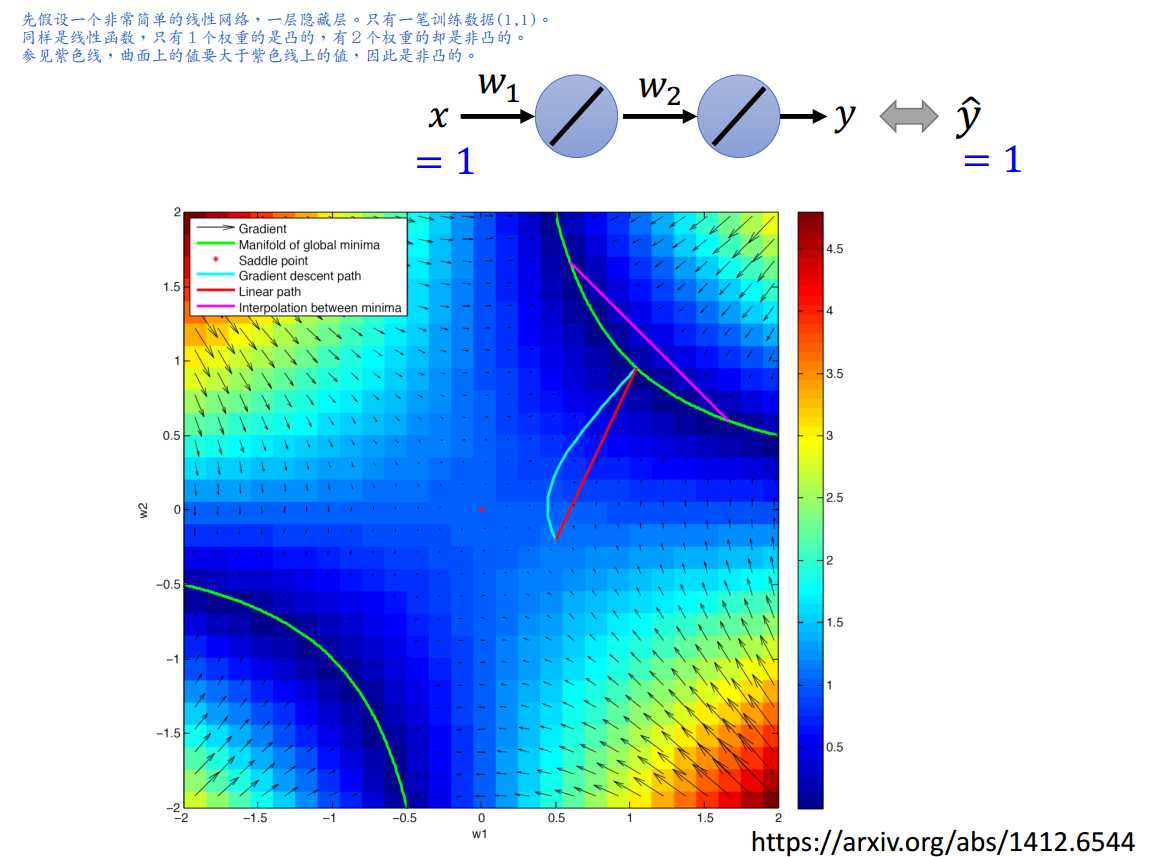




总之,可以证明,当所有隐藏层的神经元个数都不小于输入层、输出层的神经元个数时,所有的局部最小值点都是全局最小值点。
证明思路:局部最小值点处损失函数值为0,全局最小值点处损失函数值也是0,那么局部最小值点就是全局最小值点。
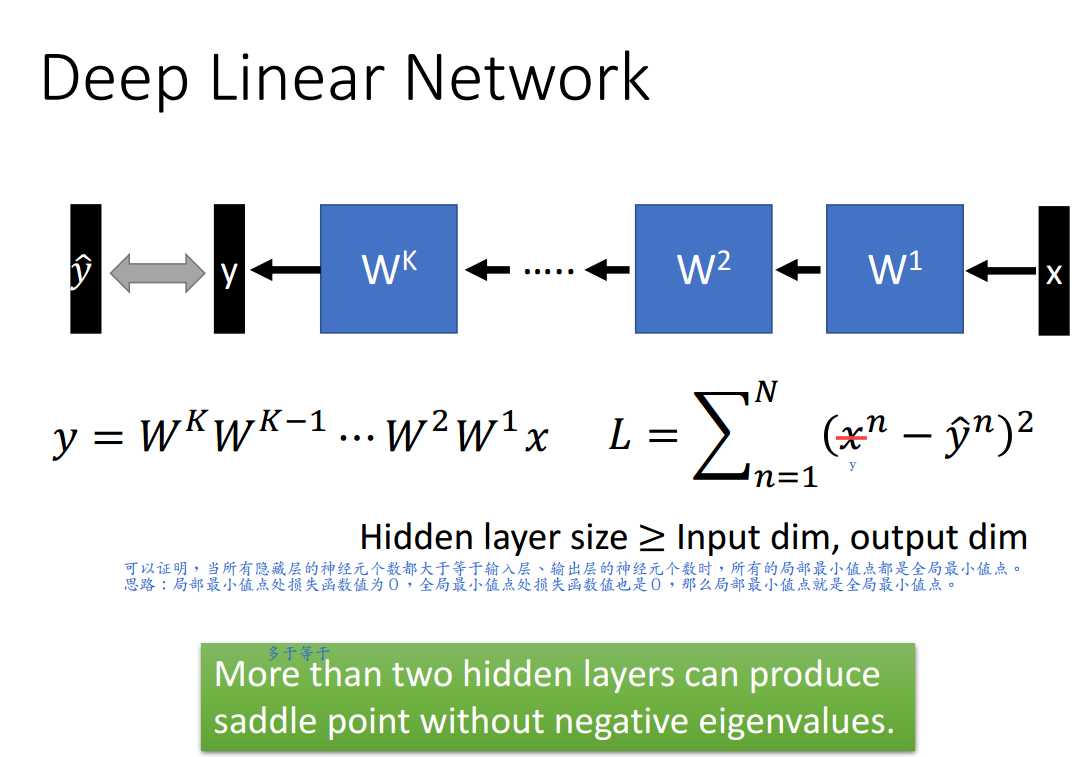
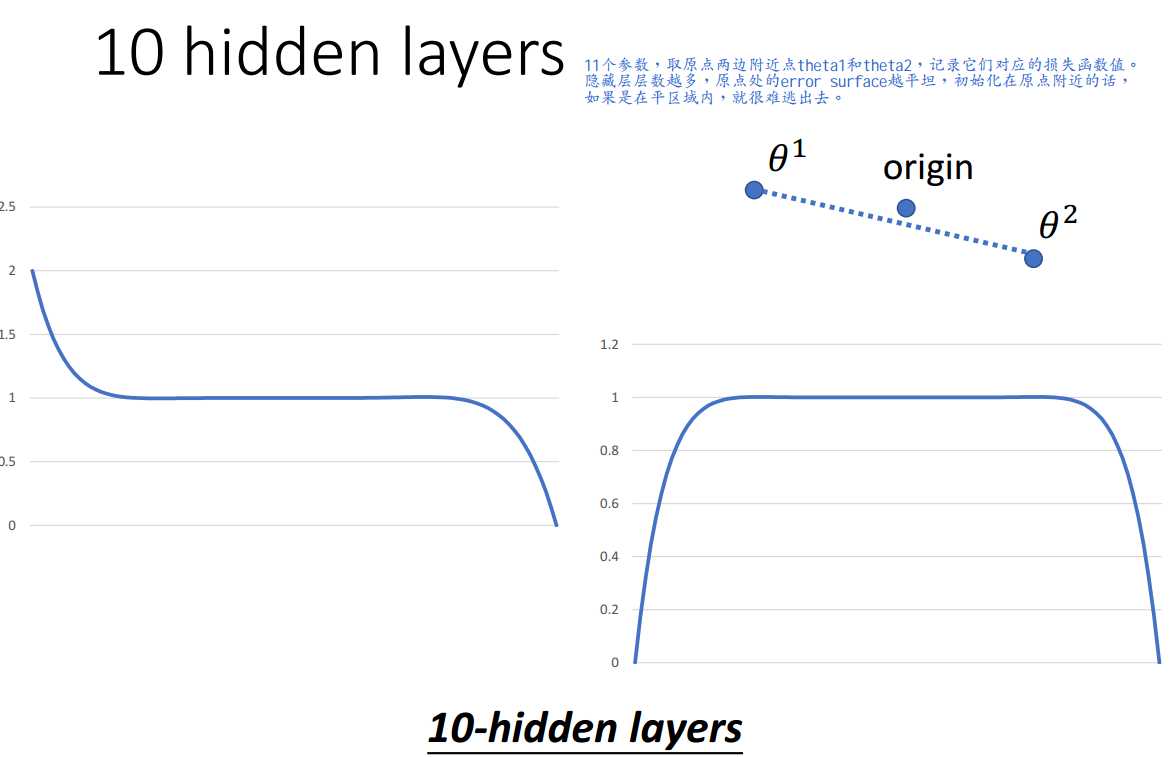
超过一层隐藏层就能产生0特征值的鞍点,有平区域,处理起来较为麻烦。
深度非线性网络有局部最小值点吗?
证明局部最小值点不存在很难,但证明其存在却很简单,只要找出一个局部最小值点即可。
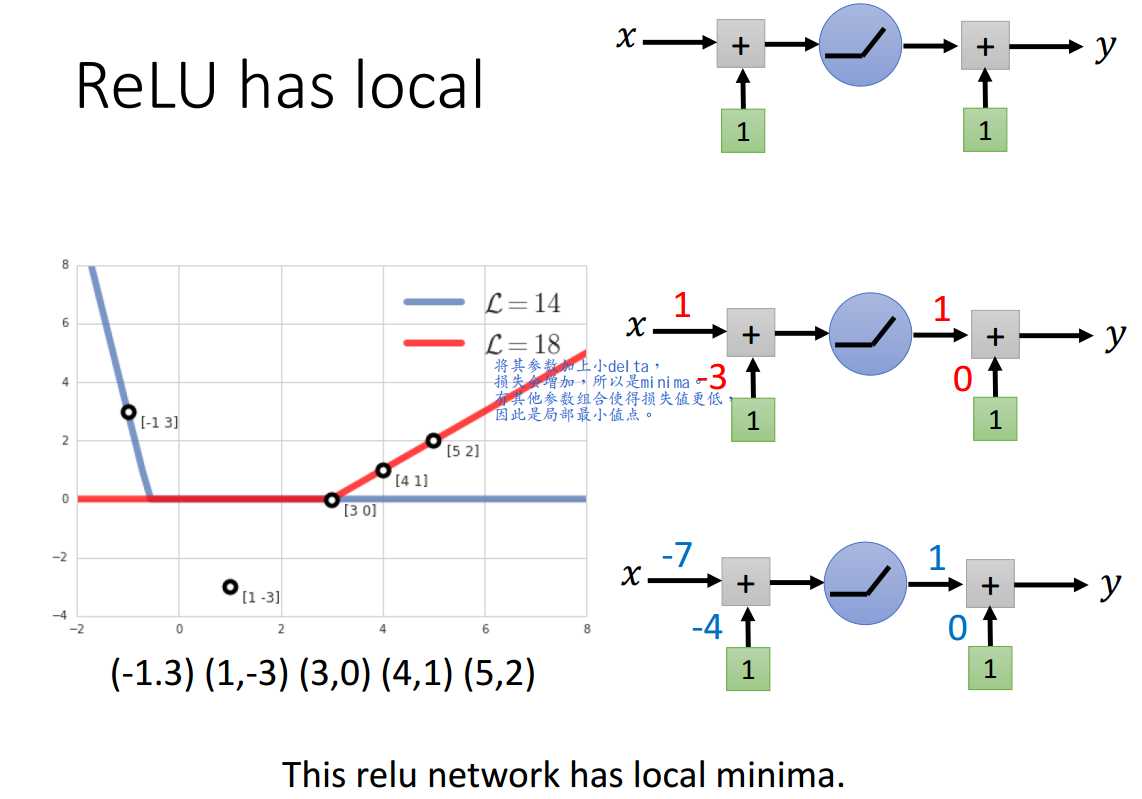
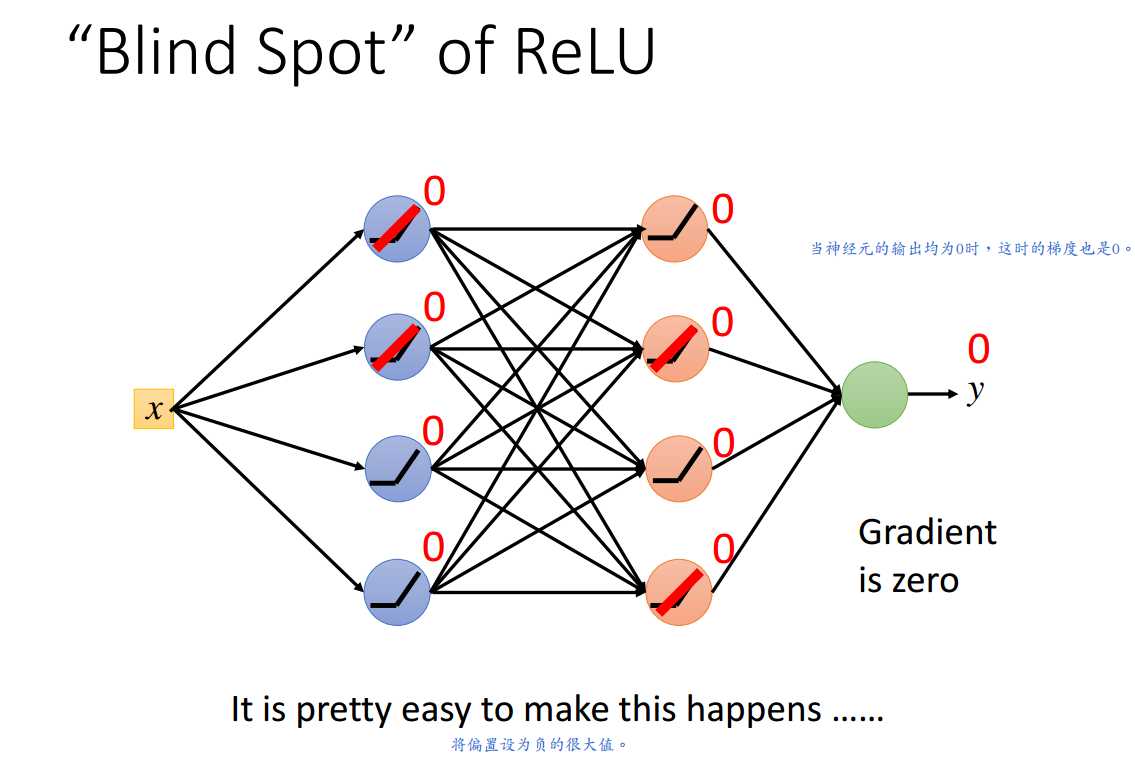
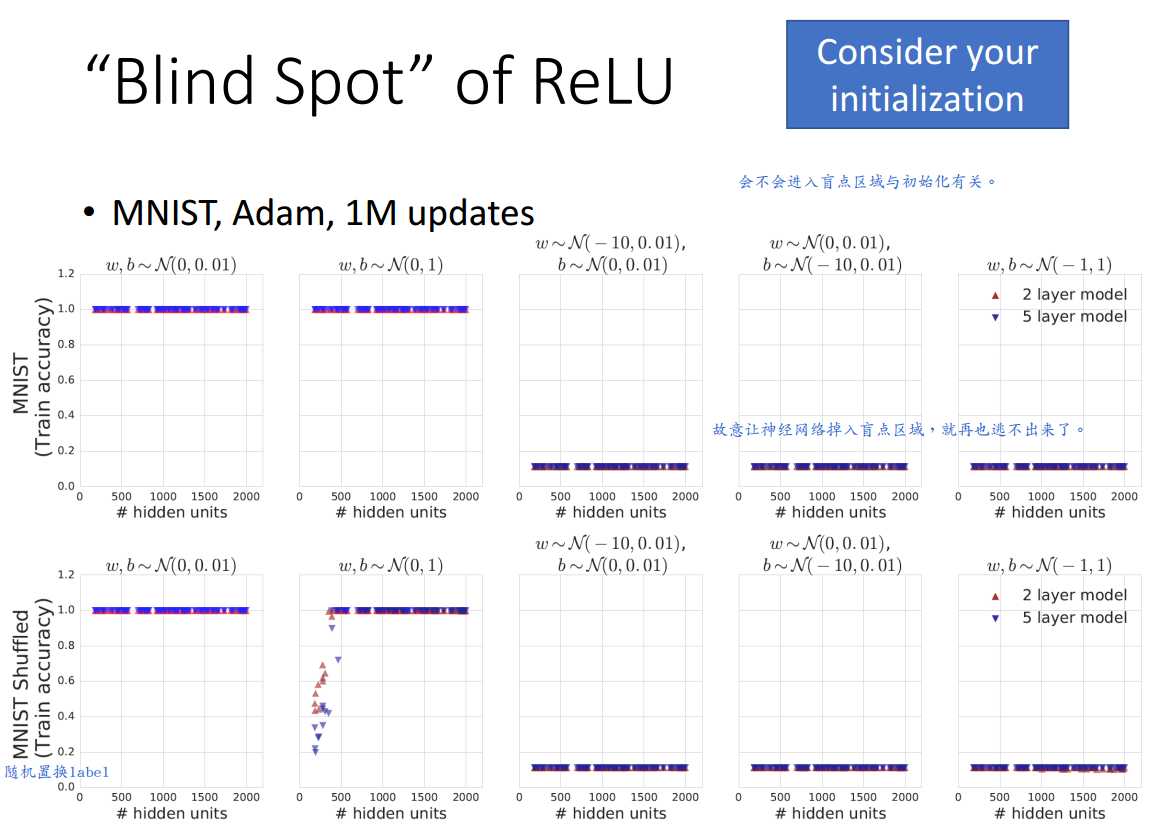
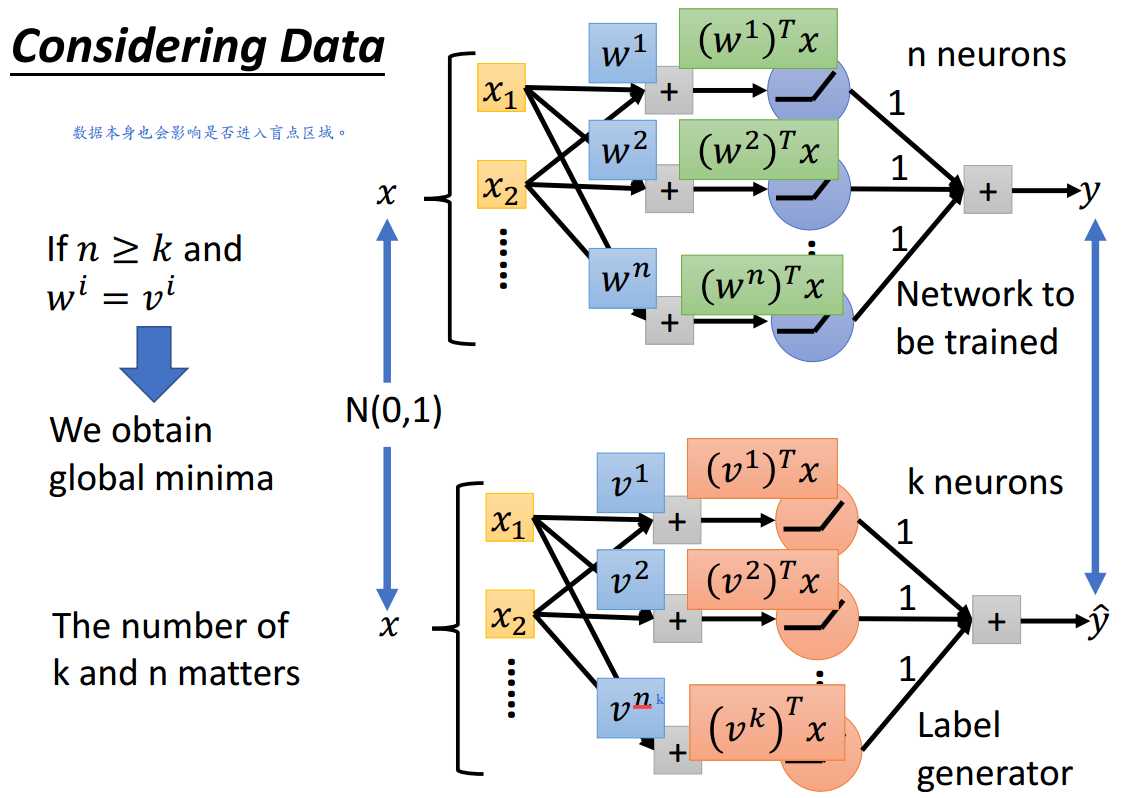
以ReLU为例。
ReLU是有局部最小值点的。
参见ReLU的盲点状态,是否进入盲点状态是与参数的初始化方式以及数据本身有关系的。
所以,以后要是有关于找到深度非线性网络的全局最小值点的理论出现,格式参考图3-6。

几乎所有的局部最小值点和全局最小值点有相似的损失函数值,因此找到一个局部最小值点已经足够好了。
先来分析Hessian矩阵,假设神经网络有N个参数,那么其对应的Hessian矩阵有N个特征值。
假设每个特征值为正、为负的概率各为0.5。

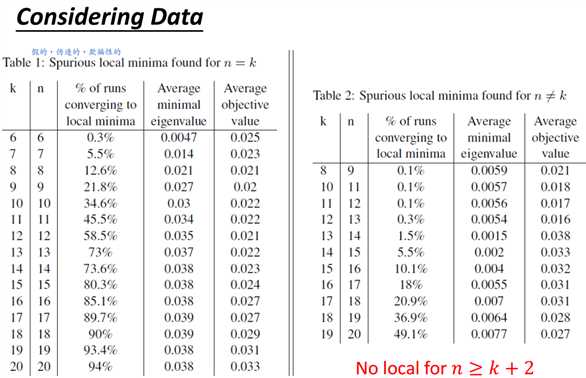
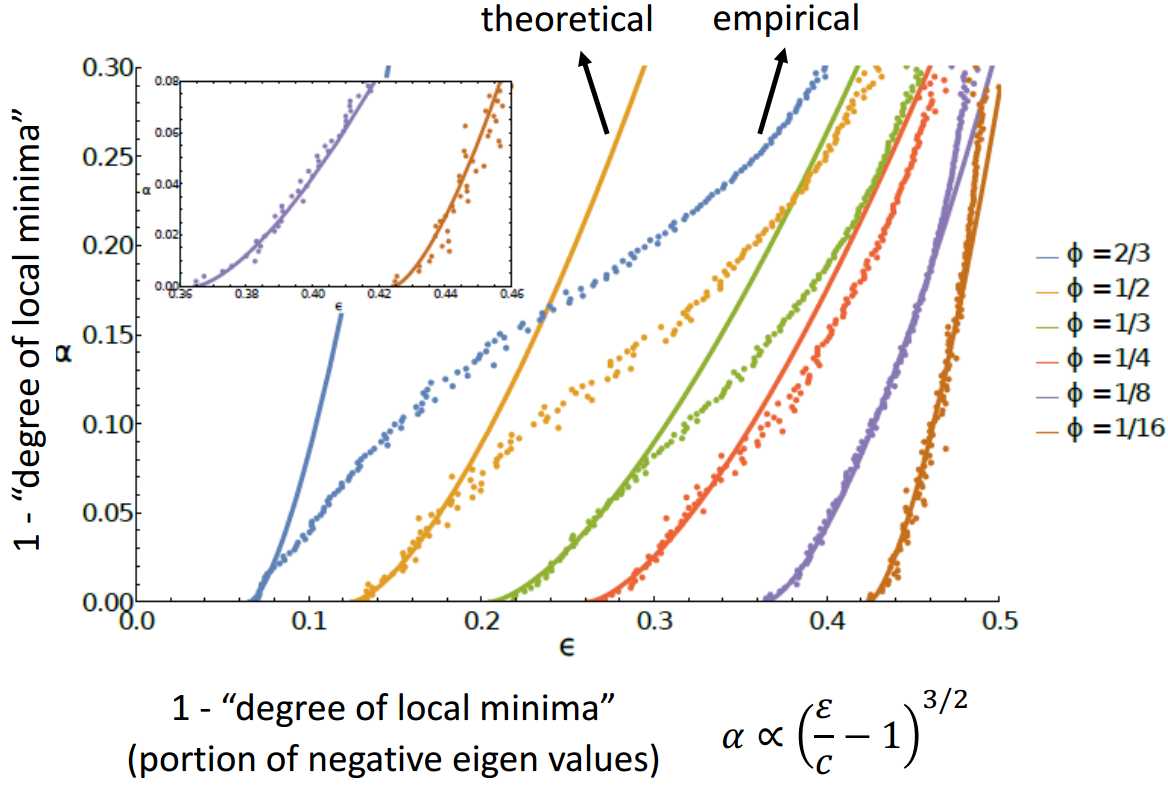
如图4-1所示,当这个网络非常大时,很难遇到局部最小值点,鞍点才是我们需要担心的。
特征值取负的几率与当前的损失值有关,损失值越大,有越多的路线使得损失下降,特征值取负的可能性越大。
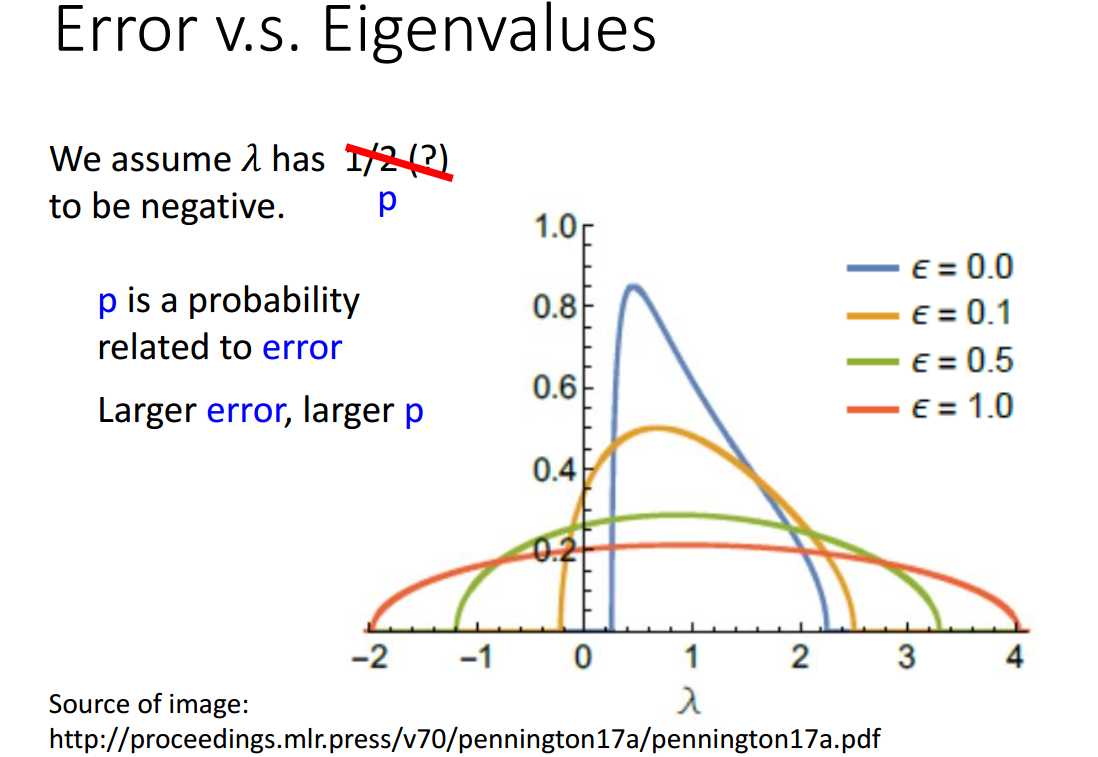
因此,鞍点比较容易出现在损失值大的地方,而局部最小值比较容易出现在损失值小的地方。

下面是一些实验结果,说明无论是理论上还是实验上,特征值取负值的几率与损失值大小成正比。
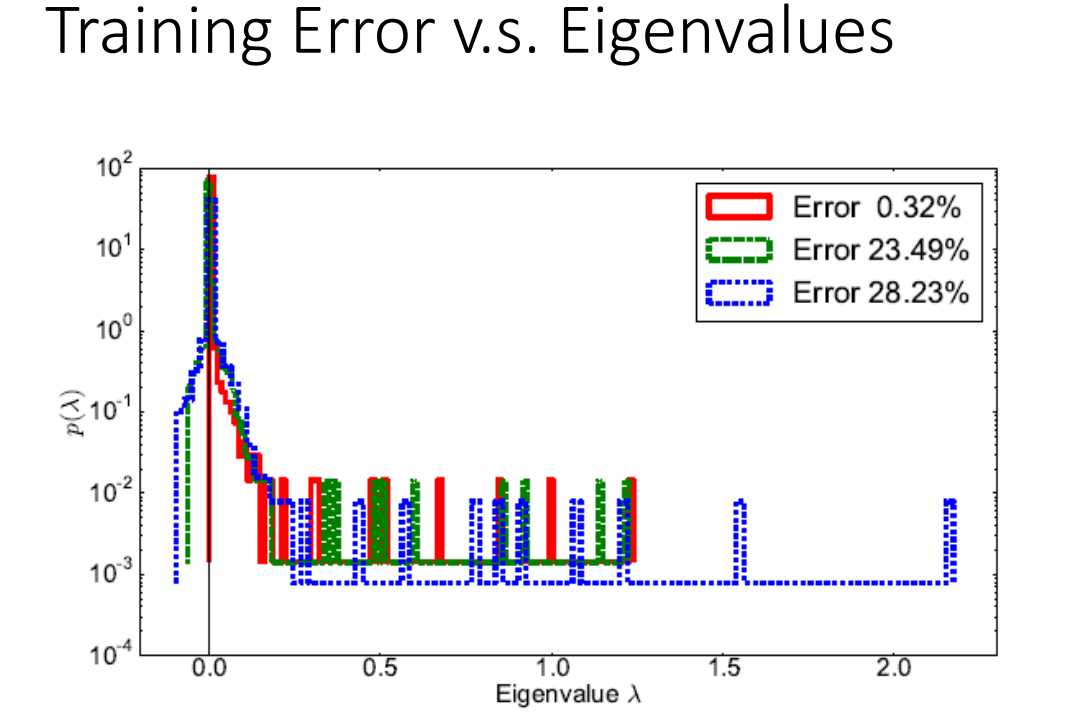
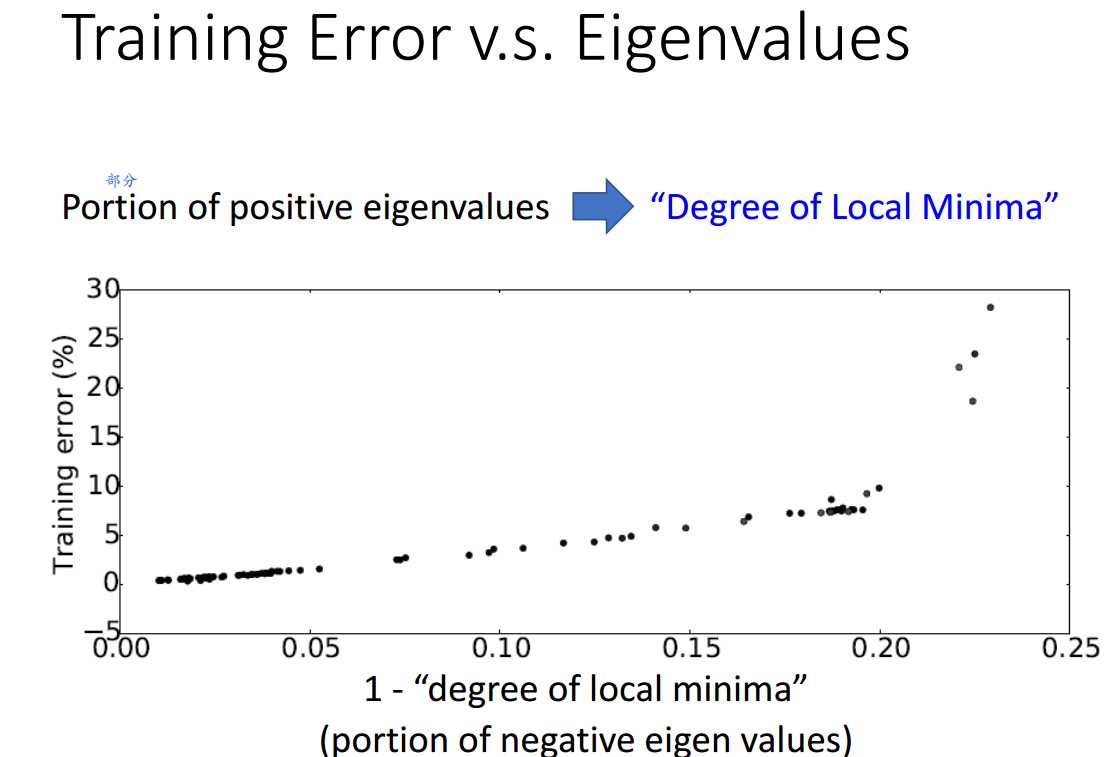
标签:关键点 color oss 为什么 AC 存在 col 结果 神经元
原文地址:https://www.cnblogs.com/cherrychenlee/p/8974821.html