标签：欧氏距离 空间 求导 bsp 思想 概率 表示 经验 out
素数：质数（prime number）又称素数，有无限个。在大于1的自然数中，除了1和它本身以外不再有其他因数。
欧拉函数：对正整数n，欧拉函数是小于n的正整数中与n互质的 数 的数目。
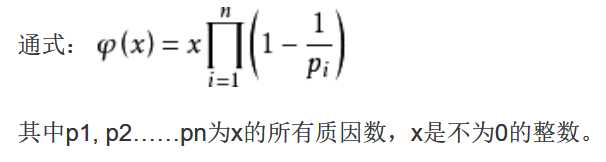
从上式来看，要先找到 x 的所有的质因数。然后才能用上式求其欧拉函数。
注意：每种质因数只一个。 比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4
极大似然估计：
极大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。
欧氏距离：
欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
为点
与点
之间的欧氏距离；
为点到原点的欧氏距离。
最小二乘法（最小平方法）：
https://blog.csdn.net/bitcarmanlee/article/details/51589143
最小二乘估计法，又称最小平方法，是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘估计法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
假设身高是变量X，体重是变量Y，我们都知道身高与体重有比较直接的关系。生活经验告诉我们：一般身高比较高的人，体重也会比较大。但是这只是我们直观的感受，只是很粗略的定性的分析。在数学世界里，我们大部分时候需要进行严格的定量计算：能不能根据一个人的身高，通过一个式子就能计算出他或者她的标准体重？
接下来，我们肯定会找一堆人进行采用（请允许我把各位当成一个样本）。采样的数据，自然就是各位的身高与体重。（为了方便计算与说明，请允许我只对男生采样）经过采样以后，我们肯定会得到一堆数据(x1,y1),(x2,y2),?,(xn,yn)，其中x是身高，y是体重。
得到这堆数据以后，接下来肯定是要处理这堆数据了。生活常识告诉我们：身高与体重是一个近似的线性关系，用最简单的数学语言来描述就是y=β0+β1x。于是，接下来的任务就变成了：怎么根据我们现在得到的采样数据，求出这个β0与β1呢？这个时候，就轮到最小二乘法发飙显示威力了。
为了计算β0,β1的值，我们采取如下规则：β0,β1
应该使计算出来的函数曲线与观察值的差的平方和最小。用数学公式描述就是：
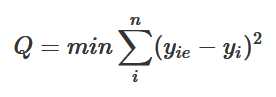
其中，yie表示根据y=β0+β1x估算出来的值（估计值），yi是观察得到的真实值。
求导，结束。
标签：欧氏距离 空间 求导 bsp 思想 概率 表示 经验 out
原文地址：https://www.cnblogs.com/quietwalk/p/8871693.html
