标签:poi 一个 列队 sed line .com ace end div
传送门:https://www.luogu.org/problemnew/show/P2161

splay
的确有线段树/树状数组的做法,但我做的时候脑残没想到
我们可以考虑写一个类似NOIP2017D2T3列队那道题那样的带分裂的平衡树
考虑用splay维护每一条线段的左端点和右端点
因为我们题目的意思保证了在平衡树里的线段不相交,所以我们可以考虑以下的性质
每一条线段作为一个点放入平衡树中,维护其L,R,并记录它是空白线段还是有预约的线段
我们要查询一段区间,设这个区间为LX,RX
我们目的是将与[LX,RX]这个线段相交的线段提取出来
那么我们就需要提取右端点<LX的线段到根,左端点>RX的线段到根的下面
根据我们平衡树维护区间的经验,根的右节点的左子树即为被包括的线段
图示如下
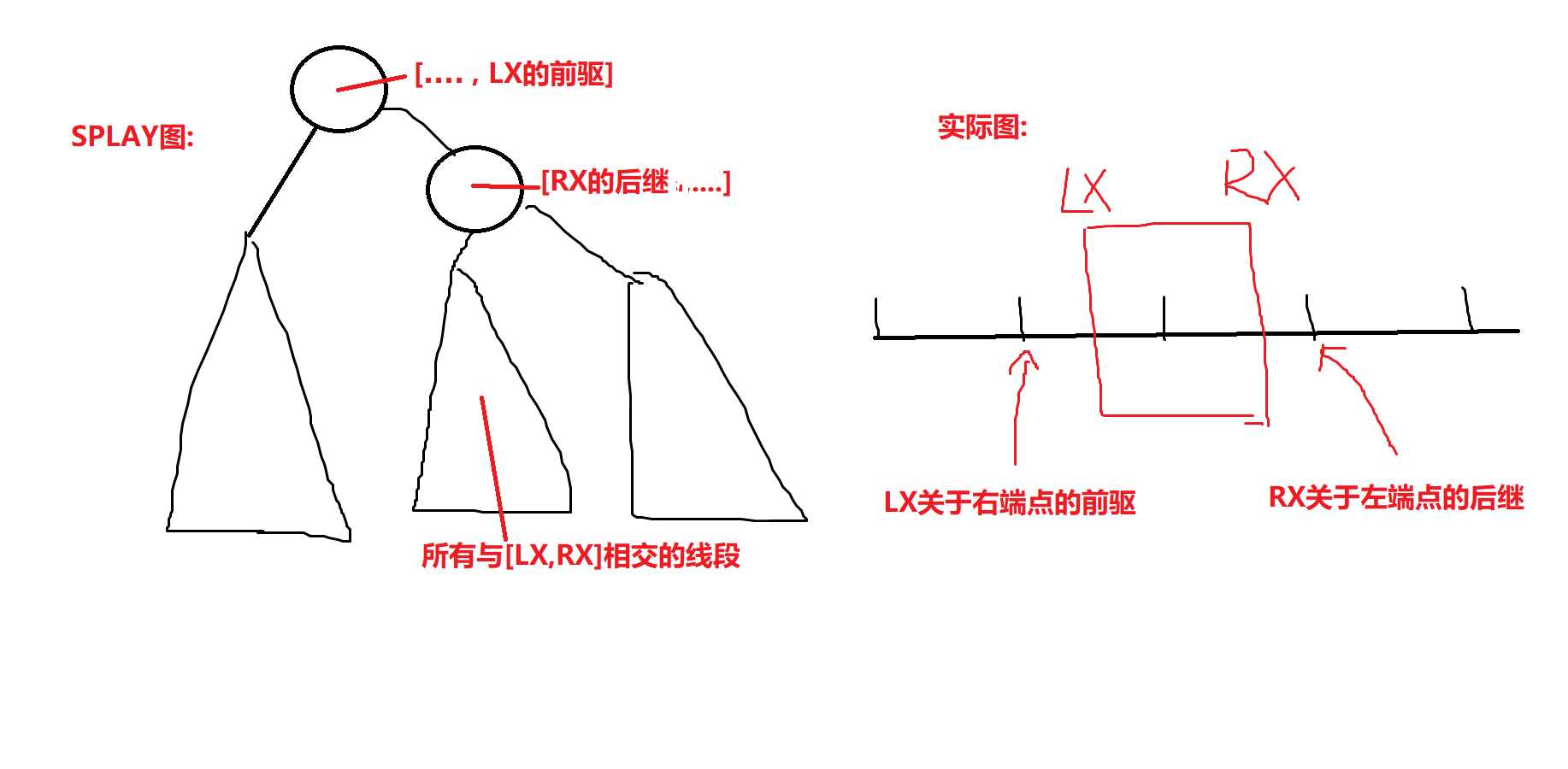
接下来的就很暴力了
我们可以直接遍历一遍被包括的子树,统计一下有多少条线段是已经预约过的
因为我们会把一整颗子树换成3个点,时间复杂度均摊意义下还是nlogn的
然后直接把一整颗子树删掉,换上我们新的线段:
[前驱+1,LX-1],空白
[LX,RX],有预约
[RX+1,后继-1],空白
注意讨论是否存在那两条空白就好
预处理加入[0,LEN-MAX]就OK了

//Luogu P2161 [SHOI2009]会场预约 //May,2ed,2018 //splay维护类区间 #include<iostream> #include<cstdio> using namespace std; long long read() { long long x=0,f=1; char c=getchar(); while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();} while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();} return x*f; } const int N=800000+1000; const int inf=0x3f3f3f3f; const int TMAX=100000; struct SPLAY { #define root son[0][1] int son[N][2],fa[N],l[N],r[N],tot; bool used[N]; inline void rotate(int x,int type) { int y=fa[x],z=fa[y]; fa[x]=z,son[z][y==son[z][1]]=x; fa[son[x][type]]=y,son[y][!type]=son[x][type]; fa[y]=x,son[x][type]=y; } void splay(int x,int to) { while(fa[x]!=to) { if(x==son[fa[x]][fa[x]==son[fa[fa[x]]][1]] and fa[fa[x]]!=to) rotate(fa[x],x==son[fa[x]][0]), rotate(x,x==son[fa[x]][0]); else rotate(x,x==son[fa[x]][0]); } } inline void Init() { root=++tot,fa[root]=0; son[root][1]=++tot,fa[tot]=root; l[tot]=1,r[tot]=TMAX; son[tot][1]=++tot,fa[tot]=son[root][1]; l[tot]=r[tot]=TMAX+1; } int FindPre(int x)//返回位置 { int now=root,ans=-inf,p=0; while(now!=0) if(r[now]>=x) now=son[now][0]; else { if(r[now]>ans) ans=r[now],p=now; now=son[now][1]; } return p; } int FindNxt(int x)//返回位置 { int now=root,ans=inf,p=0; while(now!=0) if(l[now]>x) { if(l[now]<ans) ans=r[now],p=now; now=son[now][0]; } else now=son[now][1]; return p; } int Count(int x) { if(x==0) return 0; int ans=0; if(used[x]==true) ans++; ans+=Count(son[x][0]); ans+=Count(son[x][1]); return ans; } int Change(int L,int R) { splay(FindPre(L),0); splay(FindNxt(R),root); int now=son[son[root][1]][0],ans=Count(now); now=++tot,son[son[root][1]][0]=now,fa[now]=son[root][1]; l[now]=L,r[now]=R,used[now]=true; if(r[root]<L-1) { fa[++tot]=now,son[now][0]=tot; l[tot]=r[root]+1,r[tot]=L-1; } if(l[son[root][1]]>R+1) { fa[++tot]=now,son[now][1]=tot; l[tot]=R+1,r[tot]=r[son[root][1]]-1; } return ans; } #undef root }s; int n,ans; int main() { //freopen("appointment.in","r",stdin); //freopen("appointment.out","w",stdout); n=read(); s.Init(); char OP[2]; for(int i=1;i<=n;i++) { scanf("%s",OP+1); if(OP[1]==‘A‘) { int l=read(),r=read(),temp=s.Change(l,r); ans=ans+1-temp; printf("%d\n",temp); } else printf("%d\n",ans); } return 0; }

#include<iostream> #include<cstdio> using namespace std; long long read() { long long x=0,f=1; char c=getchar(); while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();} while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();} return x*f; } const int N=200000+1000; int a[N],MAX,n,ans; int main() { freopen("appointment.in","r",stdin); freopen("ans.out","w",stdout); n=read(); char OP[2]; for(int i=1;i<=n;i++) { scanf("%s",OP+1); if(OP[1]==‘A‘) { int l=read(),r=read(),temp=0; for(int j=l;j<=r;j++) { int now=j,t=j; if(a[t]!=0) { temp++; while(a[--t]==a[now]) a[t]=0; t=j; while(a[++t]==a[now]) a[t]=0; } a[j]=i; } printf("%d\n",temp); ans=ans+1-temp; } else printf("%d\n",ans); } return 0; }

#include<iostream> #include<cstdio> #include<cstdlib> using namespace std; const int N=10000; const int MAX=10000; int main() { srand(time(NULL)); freopen("appointment.in","w",stdout); int n=rand()%N+1; cout<<n<<endl; for(int i=1;i<=n;i++) { int op=rand()%2; if(op==1) { cout<<"A "; int l=rand()%MAX+1,r=l+rand()%MAX; cout<<l<<" "<<r<<endl; } else cout<<"B"<<endl; } return 0; }
[LuoguP2161[ [SHOI2009]会场预约 (splay)
标签:poi 一个 列队 sed line .com ace end div
原文地址:https://www.cnblogs.com/GoldenPotato/p/8981895.html