标签:\n || span 距离 graham term while htm get
#include <iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int n; int top; double ans; struct Point{ int x,y; }point[110],stk[110]; double dis(Point a,Point b){//求两点距离 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double cross(Point a,Point b,Point c){//向量ab与向量ac的叉积 return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y); } void find_miny(){//找point[0] Point tmp=point[0]; int flag=0; for(int i=1;i<n;i++){ if(point[i].y<tmp.y||(point[i].y==tmp.y&&point[i].x<tmp.x)){ tmp=point[i]; flag=i; } } if(flag) swap(point[0],point[flag]); } bool cmp(Point a,Point b){//点的排序 double n=cross(point[0],a,b); if(n>0||(n==0&&dis(point[0],a)<dis(point[0],b))) return true; return false; } void Graham(){//Graham扫描法 top=-1; stk[++top]=point[0]; stk[++top]=point[1]; for(int i=2;i<n;i++){ while(top&&cross(stk[top-1],stk[top],point[i])<0) top--; stk[++top]=point[i]; } } void sum(){//求凸包的周长 ans=0; stk[++top]=point[0]; for(int i=0;i<top;i++){ ans+=dis(stk[i],stk[i+1]); } } int main() { while(scanf("%d",&n)!=EOF&&n){ for(int i=0;i<n;i++){ scanf("%d%d",&point[i].x,&point[i].y); } if(n==1) { printf("0.00\n"); continue; } if(n==2) { printf("%.2f\n",dis(point[0],point[1])); continue; } find_miny(); sort(point+1,point+n,cmp); Graham(); sum(); printf("%.2f\n",ans); } return 0; }
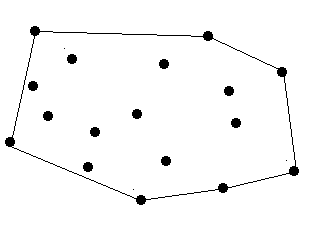
[计算几何][求解凸包]Surround the Trees
标签:\n || span 距离 graham term while htm get
原文地址:https://www.cnblogs.com/lllxq/p/8983263.html