标签:常用操作 enter 世纪 线性表 计算过程 程序 bottom 计算 允许
Stack设计与实现
Stack基本概念
栈是一种 特殊的线性表
栈仅能在线性表的一端进行操作
栈顶(Top):允许操作的一端
栈底(Bottom):不允许操作的一端
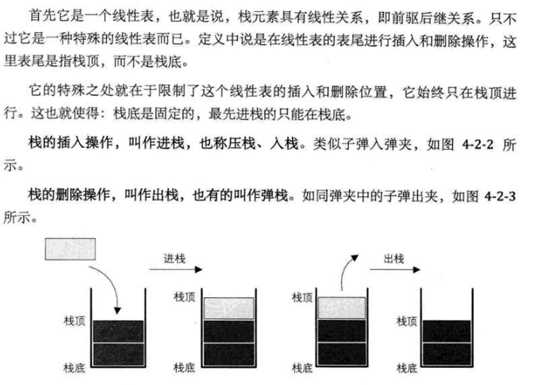
Stack的常用操作
创建栈
销毁栈
清空栈
进栈
出栈
获取栈顶元素
获取栈的大小
C语言描述=====》栈的设计与实现 人生财富库积累 |
#ifndef _MY_STACK_H_ #define _MY_STACK_H_
typedef void Stack;
Stack* Stack_Create();
void Stack_Destroy(Stack* stack);
void Stack_Clear(Stack* stack);
int Stack_Push(Stack* stack, void* item);
void* Stack_Pop(Stack* stack);
void* Stack_Top(Stack* stack);
int Stack_Size(Stack* stack);
#endif //_MY_STACK_H_ |
栈的顺序存储设计与实现
1、基本概念
|
2、设计与实现
头文件 |
#ifndef __MY_SEQLIST_H__ #define __MY_SEQLIST_H__
typedef void SeqList; typedef void SeqListNode;
SeqList* SeqStack_Create(int capacity);
void SeqStack _Destroy(SeqStack * list);
void SeqStack _Clear(SeqStack * list);
int SeqStack _Length(SeqStack * list);
int SeqStack _Capacity(SeqStack * list);
int SeqStack _Insert(SeqStack * list, SeqListNode* node, int pos);
SeqListNode* SeqList_Get(SeqList* list, int pos);
SeqListNode* SeqList_Delete(SeqList* list, int pos);
#endif //__MY_SEQLIST_H__ |
栈的链式存储设计与实现
1、基本概念
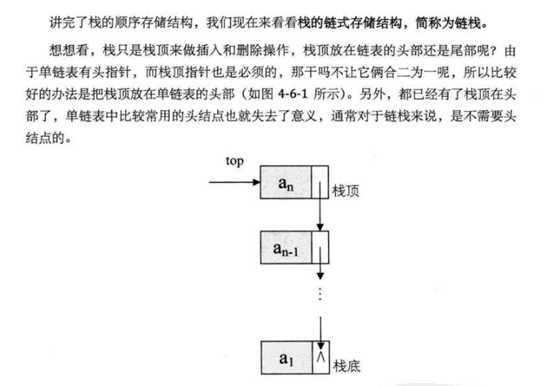
2、设计与实现
头文件 |
#ifndef _MY_LINKSTACK_H_ #define _MY_LINKSTACK_H_
typedef void LinkStack;
LinkStack* LinkStack_Create();
void LinkStack_Destroy(LinkStack* stack);
void LinkStack_Clear(LinkStack* stack);
int LinkStack_Push(LinkStack* stack, void* item);
void* LinkStack_Pop(LinkStack* stack);
void* LinkStack_Top(LinkStack* stack);
int LinkStack_Size(LinkStack* stack);
#endif //_MY_LINKSTACK_H_ |
栈的应用
应用1:就近匹配 |
几乎所有的编译器都具有检测括号是否匹配的能力 如何实现编译器中的符号成对检测? #include <stdio.h> int main() { int a[4][4]; int (*p)[4]; p = a[0]; return 0; |
算法思路 从第一个字符开始扫描 当遇见普通字符时忽略,当遇见左符号时压入栈中 当遇见右符号时从栈中弹出栈顶符号,并进行匹配 匹配成功:继续读入下一个字符 匹配失败:立即停止,并报错 结束: 成功: 所有字符扫描完毕,且栈为空 失败:匹配失败或所有字符扫描完毕但栈非空 |
当需要检测成对出现但又互不相邻的事物时 可以使用栈"后进先出"的特性 栈非常适合于需要"就近匹配"的场合 |
计算机的本质工作就是做数学运算,那计算机可以读入字符串 "9 + (3 - 1) * 5 + 8 / 2"并计算值吗? |
应用2:中缀 后缀 |
计算机的本质工作就是做数学运算,那计算机可以读入字符串 "9 + (3 - 1) * 5 + 8 / 2"并计算值吗? |
后缀表达式 ==?符合计算机运算 波兰科学家在20世纪50年代提出了一种将运算符放在数字后面的后缀表达式对应的, 我们习惯的数学表达式叫做中缀表达式===》符合人类思考习惯 |
实例: 5 + 4=> 5 4 + 1 + 2 * 3 => 1 2 3 * + 8 + ( 3 – 1 ) * 5 => 8 3 1 – 5 * + |
中缀表达式符合人类的阅读和思维习惯 后缀表达式符合计算机的"运算习惯" 如何将中缀表达式转换成后缀表达式? |
中缀转后缀算法: |
遍历中缀表达式中的数字和符号 对于数字:直接输出 对于符号: 左括号:进栈 运算符号:与栈顶符号进行优先级比较 若栈顶符号优先级低:此符合进栈 (默认栈顶若是左括号,左括号优先级最低) 若栈顶符号优先级不低:将栈顶符号弹出并输出,之后进栈 右括号:将栈顶符号弹出并输出,直到匹配左括号 遍历结束:将栈中的所有符号弹出并输出 中缀转后缀 |
|
计算机是如何基于后缀表达式计算的? 8 3 1 – 5 * + |
遍历后缀表达式中的数字和符号 对于数字:进栈 对于符号: 从栈中弹出右操作数 从栈中弹出左操作数 根据符号进行运算 将运算结果压入栈中 遍历结束:栈中的唯一数字为计算结果 |
|
栈的神奇! 中缀表达式是人习惯的表达方式 后缀表达式是计算机喜欢的表达方式 通过栈可以方便的将中缀形式变换为后缀形式 中缀表达式的计算过程类似程序编译运行的过程 |
扩展:给你一个字符串,计算结果 "1+2*(66/(2*3)+7)" 1 字符串解析 词法语法分析 优先级分析 数据结构选型===》栈还是树? |
标签:常用操作 enter 世纪 线性表 计算过程 程序 bottom 计算 允许
原文地址:https://www.cnblogs.com/love-DanDan/p/8983215.html