标签:while 相同 name 复杂 const mat top 最大流 for
吉丽的漫展有n件手办和m名警卫。建立平面直角坐标系,每个手办和警卫都可以看做一个点。警卫们的目光都朝着y轴负方向,且都有相同大小的视角。警卫可以看见自己视角内(包括边界上的点)的所有手办,不用考虑视线的遮挡。
你打算抢劫吉丽的漫展,但不可被警卫发现。为了实施这次抢劫计划,你可以事先贿赂某些警卫,让他们闭上眼睛。只要某件手办不在任何睁着眼睛的警卫的视野内,你就可以偷走它。你知道每件手办的价格,以及每位警卫需要接受多少钱的贿赂。你想知道自己的最大收益是多少。
显然是一个最大权闭合子图的模型,直接网络流复杂度不对
考虑贪心模拟网络流
我们要求的就是 \sum_{v}-maxflow
最大流可以贪心
设警卫为 \(P\),宝物为 \(Z\)
那么 \(P\) 能看到 \(Z\) 当且仅当:
\(\frac{P_x-Z_x}{P_y-Z_y}<=\frac{w}{h}\)
\(\frac{Z_x-P_x}{P_y-Z_y}<=\frac{w}{h}\)
化简得:
\(h*P_x-w*P_y<=h*Z_x-w*Z_y\)
\(h*P_x+w*P_y>=h*Z_x+w*Z_y\)
把 \(x\) 都变为 \(x*h\),\(y\) 都变成 \(y*w\) 坐标变为 \((x-y,x+y)\) 之后
条件就变成了:
\(Z_x>=P_x\,\,\&\&\,\,Z_y<=P_y\)
形如:
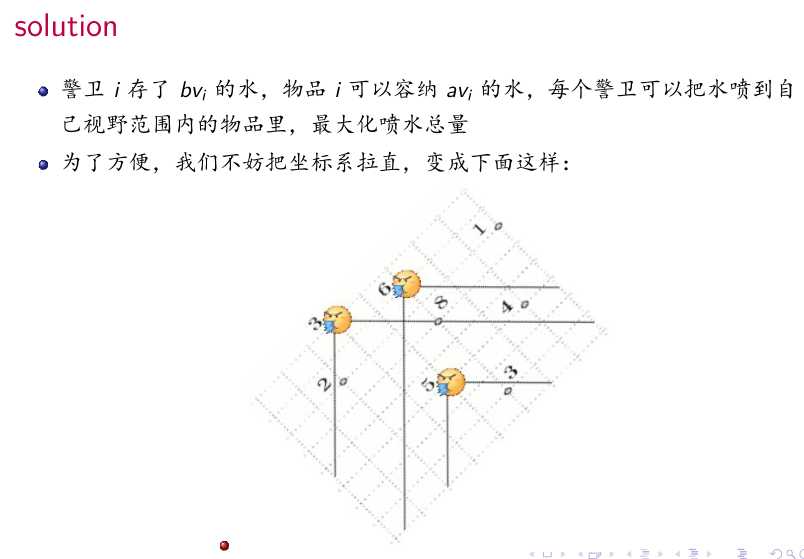
然后贪心就行了
按照 \(x\) 从大到小做,对于每一个警卫,我们希望选择 \(y\) 尽量大的宝物,因为 \(y\) 越大受到的限制越多,我们先把限制多的给处理掉
然后以此匹配下去,直到流完了或者没有可以流的了就退出, \(set\) 维护即可
#include<bits/stdc++.h>
using namespace std;
template<class T>void gi(T &x){
int f;char c;
for(f=1,c=getchar();c<'0'||c>'9';c=getchar())if(c=='-')f=-1;
for(x=0;c<='9'&&c>='0';c=getchar())x=x*10+(c&15);x*=f;
}
typedef long long ll;
const int N=4e5+10;
int n,m,W,H,v[N];ll ans=0,Y[N];
struct data{
ll x,y;int id;
inline bool operator <(const data &p)const{
if(x!=p.x)return x>p.x;
return id<p.id;
}
}p[N];
struct comp{bool operator ()(int i,int j){return Y[i]!=Y[j]?Y[i]<Y[j]:i<j;}};
set<int,comp>S;
set<int,comp>::iterator it;int top=0,st[N];
int main(){
freopen("pp.in","r",stdin);
freopen("pp.out","w",stdout);
int cnt=0;ll x,y;
cin>>n>>m>>W>>H;
for(int i=1;i<=n+m;i++){
gi(x);gi(y);gi(v[i]);
x*=H;y*=W;
p[++cnt]=(data){x-y,Y[i]=x+y,i};
}
for(int i=1;i<=n;i++)ans+=v[i];
sort(p+1,p+cnt+1);
for(int i=1;i<=cnt;i++){
if(p[i].id<=n)S.insert(p[i].id);
else{
x=p[i].id;
it=S.upper_bound(x);
if(it==S.begin())continue;
for(--it;;--it){
int t=min(v[*it],v[x]);
v[x]-=t;v[*it]-=t;ans-=t;
if(!v[*it])st[++top]=*it;
else break;
if(it==S.begin())break;
}
while(top)S.erase(st[top--]);
}
}
cout<<ans<<endl;
return 0;
}标签:while 相同 name 复杂 const mat top 最大流 for
原文地址:https://www.cnblogs.com/Yuzao/p/8984268.html