标签:界面 1.7 3.1 idt nbsp strong 定义 一个 fill
损失函数(Loss Function)是一类广义的称呼,指利用数值化的方法表现机器学习算法中产生的模型对于训练集(Training Set)的满意程度。
通常函数值越小,表示该模型预测越精准。
损失函数是一个评判标准,模型的优化训练皆是基于此标准进行,训练模型的目的就是找到一个损失函数最小的模型。

如同CIFAR10,通常数据集都以上述模式给出:
x是数据集的数组,y是和x对应的每个数据的标签的数组
一般地,损失函数可写作下式:
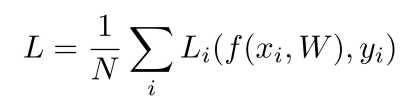
i代表了每个数据,L_i即是对于每个训练数据进行预测时得到的损失函数值,最终对N个数据的损失值进行平均。
式中f(x_i,W)的f是预测函数,W即为使用的模型。

如上为某数据集(3个数据,3个标签),矩阵为3张图片在W模型下得到的关于3个类别下的评分(分高为优)
可见,第一张图片(猫),第二张(汽车),第三张(青蛙)都是在汽车标签得分最高。
下面列举几种常见的损失函数思路:
1. SVM损失(Hinge Loss)
使用SVM的思想,即寻找最合适的分界面。只是在这里是运用的SVM多分类而不是二分类。
此时L_i的计算公式为:
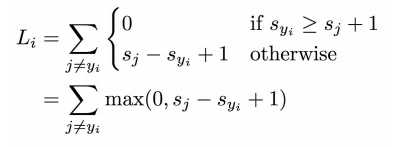
公式解释:s_y_i表示i图对应的正确标签在W下的得分,s_j表示所有不是正确标签的得分,1是一个超参数(可以自己更改选择),表示正确预测分需要超过不正确的预测某一个margin才能保证此次预测的正确性。
如第一张图(猫)正确标签是猫(记为图1),所以s_y_1=3.2,L_1=max(0,5.1-3.2+1)+max(0,-1.7-3.2+1)=2.9+0=2.9
汽车项取到2.9是因为该图片的汽车得分比猫得分高,并且加上一个安全值1,其和表示对于汽车标签的损失。青蛙项取0是因为猫的分数3.2比青蛙的分数-1.7高出超过安全值(1),预测值对于青蛙标签没有损失。
同理L_2=max(1.3-4.9+1)+max(2.0-4.9+1)=0,损失为0因为汽车的预测正确且分数皆比其他标签分数高出超过一分。
L_3=max(2.2-(-3.1)+1)+max(2.5-(-3.1)+1)=12.9
所以该模型的平均损失L=(2.9+0+12.9)/3=5.27
在python中使用该算法时,可用如下的向量化计算方法:

输入x是x_i即一张图片的向量表示,y是y_i即正确标签
W.dot(x)表示是线性分类器的矩阵点乘,W是分类器模型
margins[y]是一个小技巧,将正确标签下的损失值(一定等于1)归零,表示j≠y_i的条件。
调用一次L_i_vectorized即是求一个数据对象的损失值。
正则化
有时我们希望模型的复杂度、阶数不要太高避免出现过拟合现象,此时在L的计算式中引入一项,称为正则项
正则化后的损失函数公式如下。
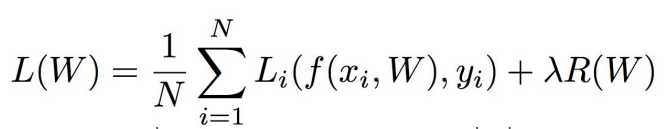
R(W)表示不同阶数的模型W在损失函数中的代价,一般W的阶数越高,R(W)值越大,即损失越大。
其思想是:若要采用阶数更高的模型W2,那么它必须克服其相对于更低阶模型W1所增加的代价λ*(R(W2)-R(W1)),λ是一个自选常数参量(超参数)
对于线性分类器W,正则函数常有以下几种形式:

2.Softmax 分类器(Cross-Entropy Loss)
Softmax分类:一般化的逻辑斯蒂回归
假设这些分数都是未标准化的对数概率
这一列表示真实图片为猫,然后判断为这三类的分数分别为3.2、5.1、-1.7。
求图片为某一类的概率: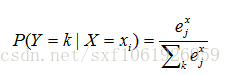
使正确分类的概率的对数最大,根据损失函数,我们要使负的正确分类概率的对数最小,所以概率对数是分数的扩展。
问:上面这个Loss的最大值、最小值?
答:看log函数就能看出来,为1的时候最小为0,为0的时候最大为无穷大。
问:刚开始训练的时候,W很小,那么损失值是多少呢?
答:是类别数分之一的对数负值,可用于检查代码
Hinge Loss VS Cross-Entropy Loss
Hinge Loss 在正确类别的得分比错误类别得分高1之后就不进行优化了,因为此时的损失函数不会再减小了。
与之相对的是Cross-Entropy Loss,根据定义,想要得到理想的概率分布,势必要让正确类别的得分趋近于正无穷,错误类别的得分趋近于负无穷,所以模型会不断的优化参数,试图去迫近这个最理想的概率分布。
标签:界面 1.7 3.1 idt nbsp strong 定义 一个 fill
原文地址:https://www.cnblogs.com/CaptainLL/p/8994332.html