标签:范围 卡尔 需要 [] 大于等于 案例 贪心算法 ase com
http://poj.org/problem?id=1328
题目大意:假设海岸是一条无限的直线。陆地在海岸线的一边,大海在另一边。每个小岛都位于海边。任何雷达装置,定位在海岸上,只能覆盖d距离,所以在海中的一个岛屿可以被半径安装覆盖,如果它们之间的距离是最大的d。我们用笛卡尔坐标系统,定义滑行是x轴。海面在x轴上方,陆地在下面。考虑到每个岛屿在海上的位置,并且考虑到雷达装置的覆盖范围,你的任务是编写一个程序来找出覆盖所有岛屿的雷达装置的最小数量。请注意,岛屿的位置用它的x-y坐标表示。输入由几个测试用例组成。每个案例的第一行包含两个整数n (1<=n<=1000)和d,其中n是海中岛屿的数量,d是雷达装置的覆盖距离。后面是n行,每个包含两个代表每个岛位置坐标的整数。然后是一个空行来分隔这些案例。输入由包含一对0的行终止。对于每个测试用例,输出一行包括测试用例编号,然后是所需的最小数量的雷达安装。“-1”安装意味着没有解决方案。
也就是说在一个笛卡尔坐标系上n个岛屿的坐标 (x,y)给出,要求用最少的雷达能够覆盖n个岛屿。当然,如果某一个岛屿的纵坐标如果大于雷达扫描半径d显然,此时输出-1。为了方便表示,我们可以将二维的(x,y)坐标表示,转化为一维的x坐标区间表示,即利用勾股定理得到每个岛屿所对应的能放置雷达的区间[ xLeft , xRight ]。
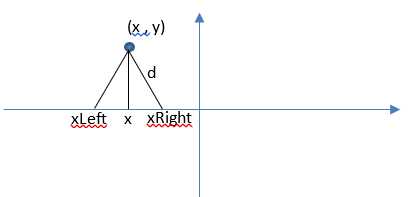
算法思想:贪心算法,贪心策略是使每一个雷达尽可能的覆盖更多的岛屿。即使雷达能覆盖更多的区间。首先,我们要对得到的区间依照xLeft从小到大进行排序,便于我们进行选择,先从最小的xLeft对应的岛屿开始,我们设置一个在x轴从左到右遍历的temp并初始化为排序后第一个岛屿的xRight(为了覆盖更多的区间)。那么接下来的一个岛屿,有三种情况:
第一种情况显然需要多加一个雷达,并置temp为下一个雷达的xRight;
第二种情况不需要加雷达,temp的值保持不变;
第三种情况不需要加雷达,但是temp的值要置为下一个雷达的xRight(这样才能覆盖此雷达);

PS:如果不了解STL <algorithm>头文件sort()函数,可以查一下,也可以自己写一个排序算法,对区间排序。
1 #include <iostream> 2 #include <algorithm> 3 #include <cmath> 4 using namespace std; 5 struct coordinate//存储x轴区间的结构 6 { 7 double xLeft; 8 double xRight; 9 }; 10 bool compare(coordinate a_coordinate,coordinate b_coordinate)//sort第三个参数 11 { 12 return a_coordinate.xLeft <= b_coordinate.xLeft; 13 } 14 int main(void) 15 { 16 int n;//n个岛 17 double d;//雷达扫射半径 18 int testCase = 0;//测试案例数 19 while (cin >> n >> d && (n != 0 && d != 0)) 20 { 21 coordinate *coor = new coordinate[n + 1]; 22 bool sovable = true;//默认可解 23 if (d < 0) sovable = false; 24 testCase++;//测试案例数+1 25 double x, y; 26 for (int i = 1; i <=n; ++i) 27 { 28 cin >> x >> y; 29 if (y > d)//如果岛的y轴坐标超出雷达扫射半径,问题不可解 30 sovable = false; 31 double temp = sqrt(d*d - y * y);//勾股定理求雷达覆盖能达到距离 32 coor[i].xLeft = x - temp; 33 coor[i].xRight = x + temp; 34 } 35 sort(coor + 1, coor + n +1 , compare);//按左值从xiao到da排序 36 int leida = 1;//至少一个雷达 37 double temp=coor[1].xRight;//从最左边的那一段的右端开始遍历 38 for (int i = 2; i <=n; ++i) 39 { 40 if (temp<coor[i].xLeft)//如果第二段的左值小于第一段右值 41 { 42 temp = coor[i].xRight; 43 leida++;//显然需要增加雷达 44 } 45 else//如果第二段的左值大于等于第一段右值 46 { 47 if (temp>coor[i].xRight)//如果第二段的右值小于第一段右值 48 { 49 temp = coor[i].xRight;//更新遍历的值 50 } 51 else 52 { 53 54 } 55 } 56 } 57 leida = sovable ? leida : -1;//如果问题不可解赋值-1 58 cout << "Case " << testCase << ": " << leida << endl;//End 59 delete[] coor; 60 coor = NULL; 61 } 62 return 0; 63 }
标签:范围 卡尔 需要 [] 大于等于 案例 贪心算法 ase com
原文地址:https://www.cnblogs.com/DA799422035/p/8994720.html