标签:建表 src ima 比较 常用 灵活 strong break 表达式树
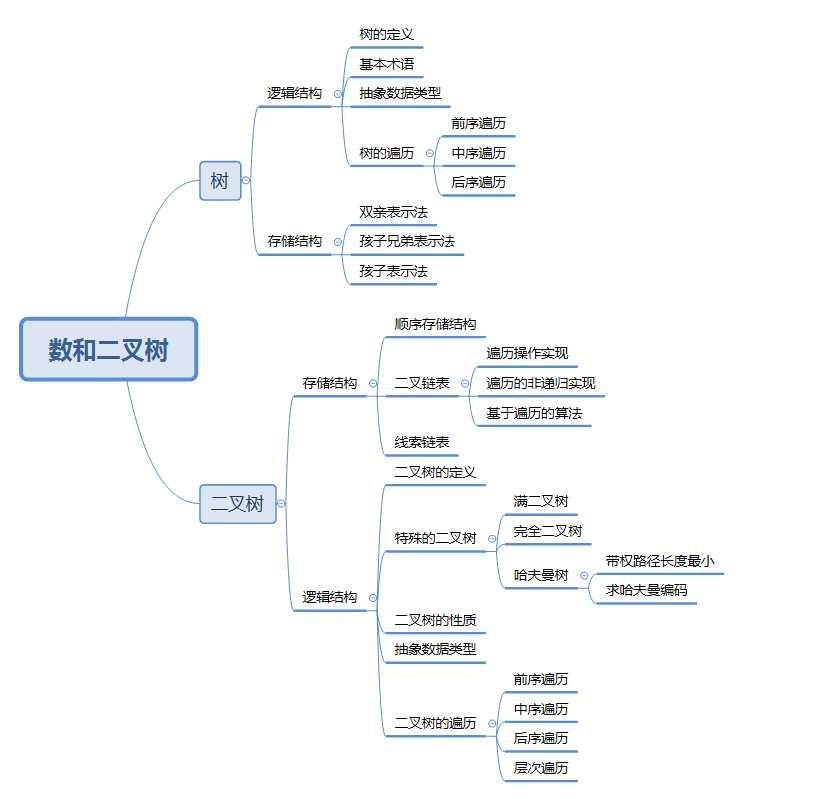
树结构十分的灵活,其大部分时间可以保证操作的运行平均时间复杂度为O(logN),可以缩小搜索范围。
这是一些树结构的常用术语:
1、结点:树中的数据元素都称之为结点
2、根:最上面的结点称之为根,一颗树只有一个根且由根发展而来,从另外一个角度来说,每个结点都可以认为是其子树的根
3、父亲:结点的上层结点,如图中,结点K的父亲是E、结点L的父亲是G
4、兄弟:具有相同父亲的结点称为兄弟,图中F、G、H互为兄弟
5、结点的度:结点所拥有的子树的个数称之为结点的度,如结点B的度为3
6、树叶:度为0的结点,也叫作终端结点,图中D、K、F、L、H、I、J都是树叶
7、分支结点:度不为0的结点,也叫作非终端结点或内部结点,图中根、A、B、C、E、G都是分支结点
8、结点的层次:从根节点到树中某结点所经路径上的分支树称为该结点的层次,根节点的层次规定为1,其余结点的层次等于其父亲结点的层次+1
9、树的深度:树中结点的最大层次数,图中树的深度为4
学习这个结构的时候遇到了许多困难,首先二叉树的遍历,一直弄不明白,后来不断的研究,不断地试验终于弄懂了。然后在画线索二叉树的时候又遇到了麻烦,不过这些都最后完成了。
创建树
{
定义树T
定义i=0用来计数
定义队列Q用来存放树的节点
当str[i]!=0
{
BT申请空间
将str[i]赋予BT->data
初始化左右孩子
BT节点入队
}
否则 重新进入函数
BT=NULL
while队列Q不为空
{
将队头元素赋给树T
元素出队
如果str[i]==‘#‘||str[i]==‘0‘
令左孩子为空
否则
{
给T的左子树申请空间
将str[i]赋给左孩子
初始化左子树的左右孩子
T的左孩子入队
}
i++;
如果str[i]==‘#‘||str[i]==‘0‘
T的左孩子初始化
否则
{
给T的右子树申请空间
将str[i]赋给右孩子
初始化右子树的左右孩子
T的右孩子入队
}
i++;
}
}


这道题一遍过,当时参考了同学的代码,自己理解后又打了一遍,一次通过。
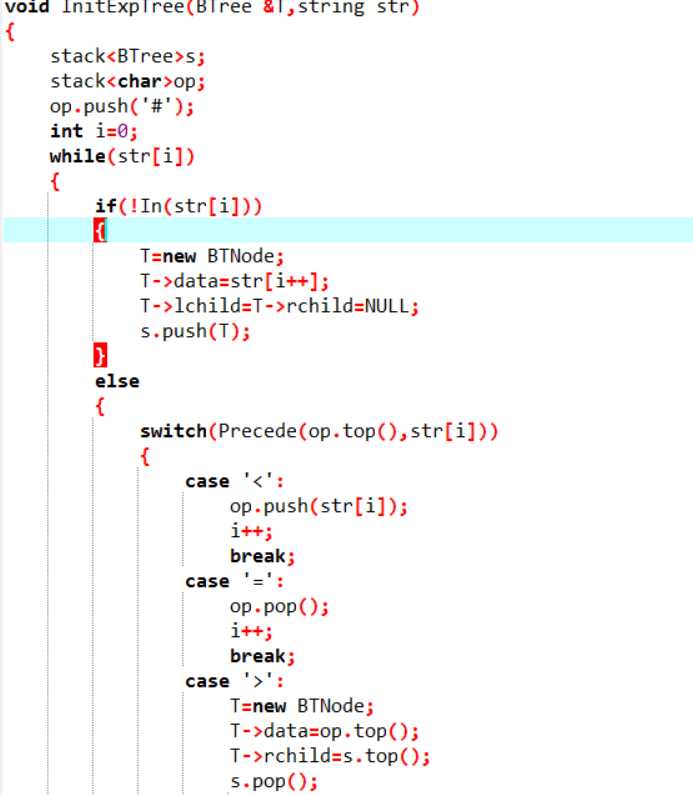
函数:建表达式的二叉树
定义栈s BTree
栈 char op
# 入栈op
定义i=0
while(str[i]不为‘/0’){
当str[i]不是运算符{
给树的节点T申请空间
值为str[i++]
令T的左右子树为空
T入栈S
}
否则{
switch(比较op.top(),str[i]的优先级
当返回 ‘<‘:
入栈(str[i])->op;
i++;
break;
当返回 ‘=‘:
取栈顶
i++;
break;
当返回 ‘>‘:
T=new BTNode;
T->data=op栈顶元素
T->rchild=s栈顶元素
s出栈
T->lchild=s栈顶元素
s出栈
T入栈S
op出栈
break;
}
}
}
while(op栈顶元素不为#)
{
T=new BTNode;
T->data=op栈顶元素
T->rchild=S栈顶元素
S出栈
if(S不为空)
{
T左孩子等于s栈顶元素
s出栈
}
T入栈S
op出栈
}
T为s栈顶元素
函数:计算表达式树
定义 sum=0,a,b
当T的左右子树都不为空时{
返回 T->data-‘0‘
}
a=递归计算左子树
b=递归计算右子树
switch(T->data)
{
+ return a+b break
- return a-b break
* return a*b break
/
当b<1且b-1不为0{
输出 "divide 0 error!"
}
return a/b
break
}



老错误!!!没有改c++提交 。部分正确是因为在输出的时候出错,答案错误。后经询问大佬改对了。
定义顺序为由小到大的优先队列L
定义整形变量 n,a,i
cin n
for ( i=0 i<n i++){
cin a
a入队
}
定义 sum为0;
while(l的长度不为1){
定义x 将队头元素值赋给x
出队
定义y 将队头元素值赋给y
出队
sum+=x+y;
x+y入队
}
输出sum
return 0;
先是没调成c++提交,然后运行时错误了,一开始不知道是什么情况,后来发现循环条件弄错了应为L的长度不为1。

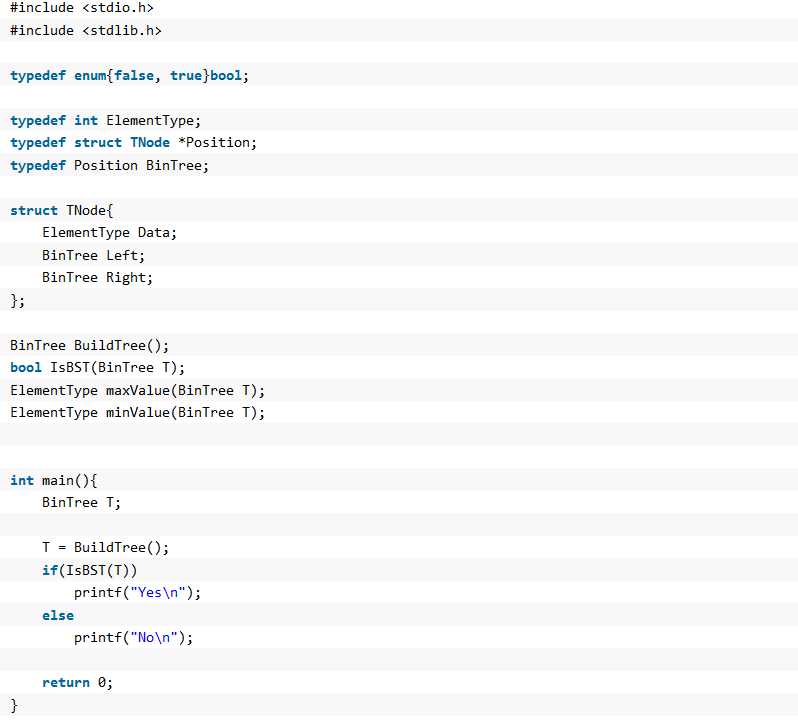
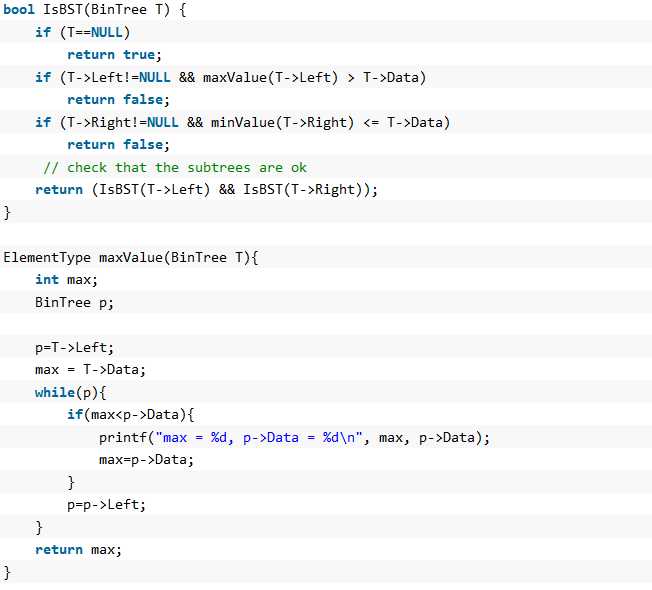
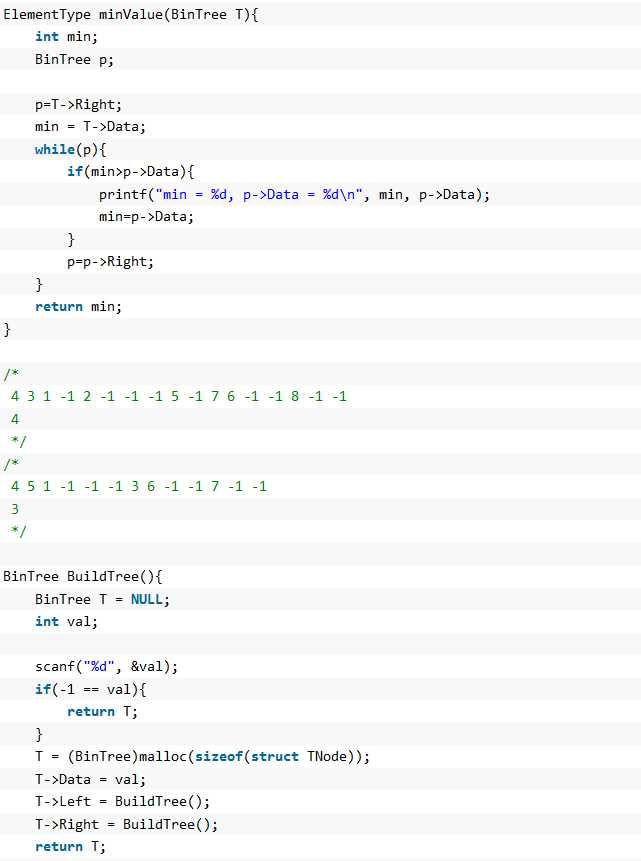
此代码的功能是判断是否为二叉搜索树。
代码地址:https://blog.csdn.net/u013243314/article/details/73714132
标签:建表 src ima 比较 常用 灵活 strong break 表达式树
原文地址:https://www.cnblogs.com/gaof/p/8994536.html