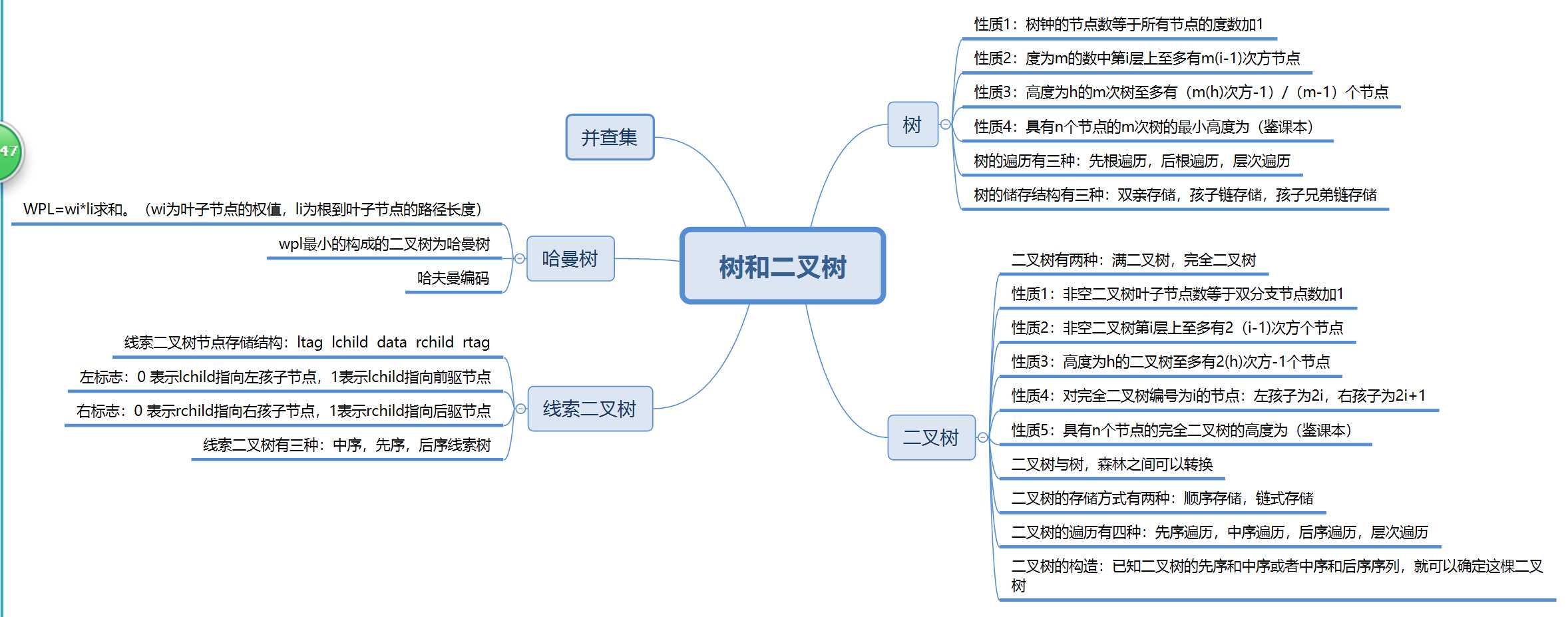
遍历树
若BT->Left==NULL&&BT->Right==NULL,则为叶子节点输出
然后再递归判断BT的左孩子节点和右孩子节点是否为叶子节点

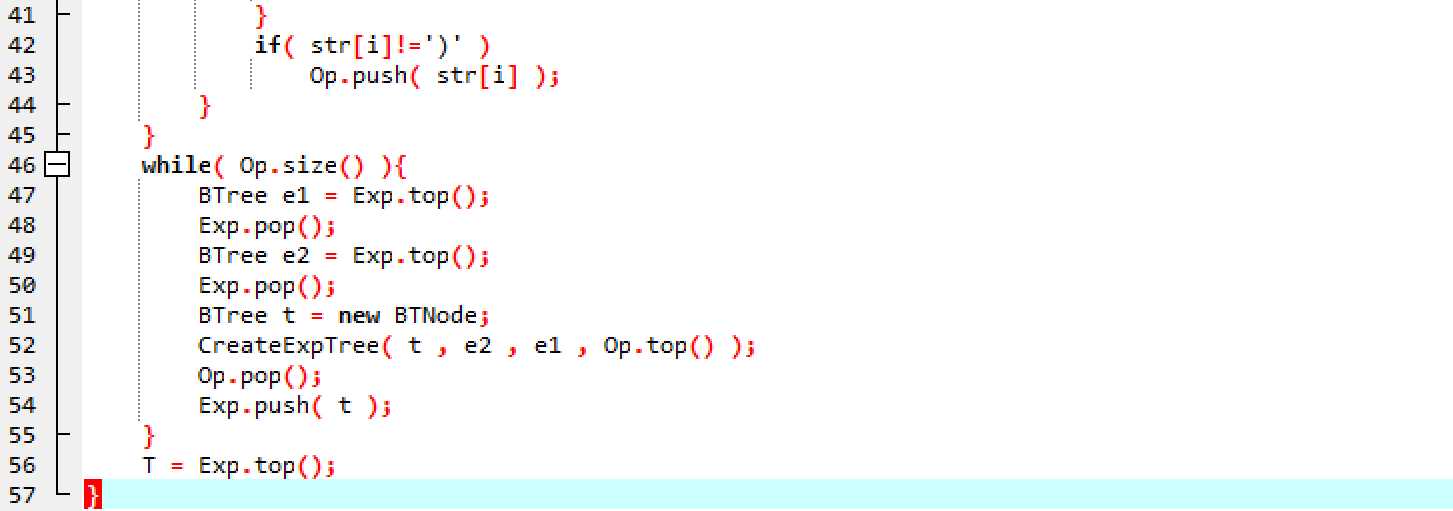
计算二叉树
若T->data为数字字符，则返回对应的数值
若T->data为运算符ch，则利用递归返回EvaluateExTree( T->lchild ) ch  EvaluateExTree( T->rchild )的值。
特别注意的是ch==/时，需要对分母EvaluateExTree( T->rchild )进行判断，若为0时，则提示错误。

构建表达式树
建立两个栈，一个存放运算符，一个存放树节点
遍历for i=0 to str[i]==0
    若str[i]为数字字符，则创建一个data为str[i]，左右孩子都NULL的节点t，并将t推进树栈。
    若str[i]为运算字符
        则将str[i]对应的运算符与运算符栈栈顶的运算符，比较优先级。
        若栈顶的运算符优先级高，则两次取出树栈的栈顶，创建节点CreateExpTree( t , e2 , e1 , Op.top() )，再将t存入树栈，再把运算符的栈顶出栈，直到运算符栈顶与str[i]优先级相等。
end for
while(op.size())
     把运算符栈中的剩余运算符一个一个出栈，并且分别创建节点。
end
将T指向创建的表达式树。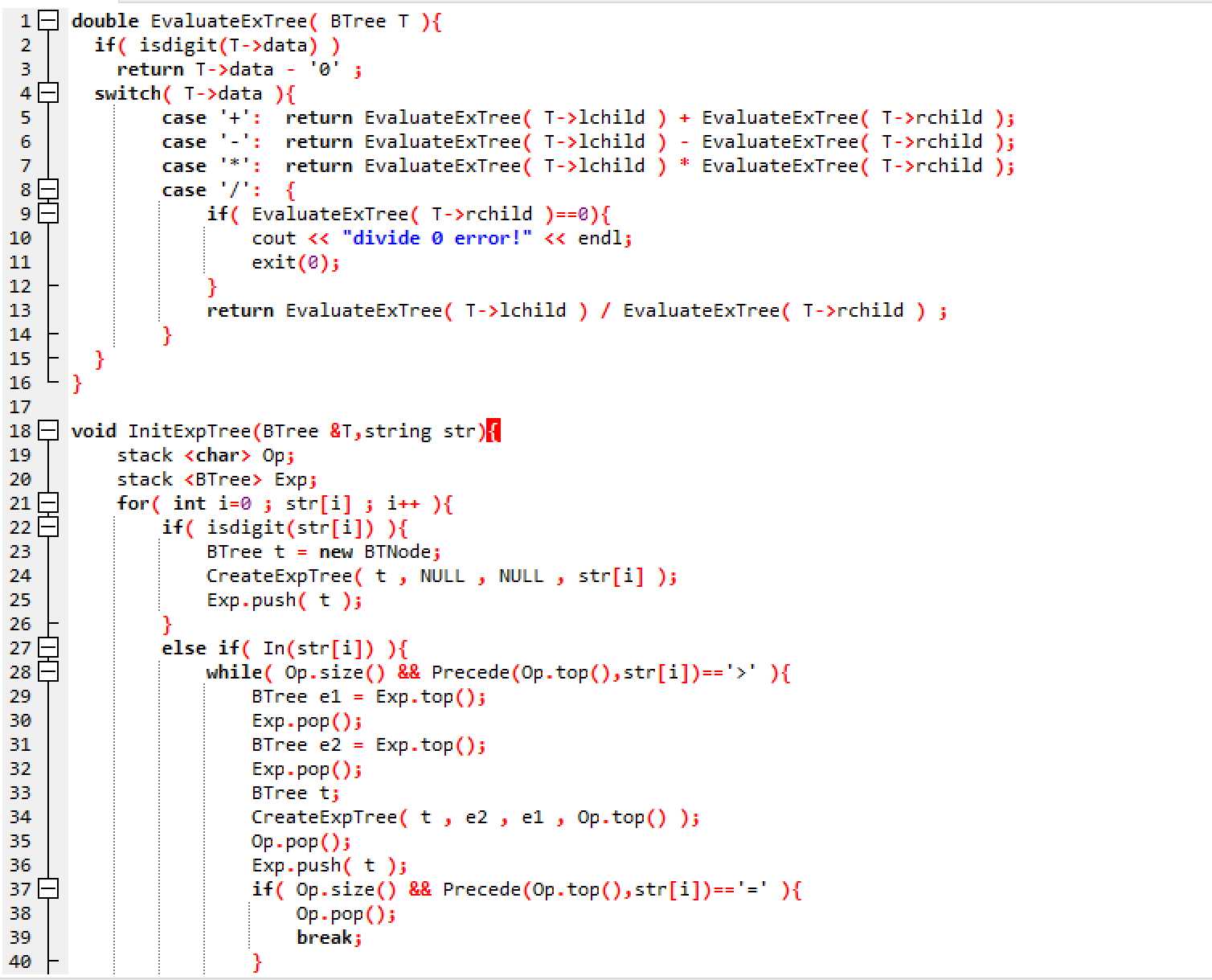

利用递归创建二叉树
    因为第i个节点的左孩子为2i,右孩子为2i+1
    所以利用这个关系将顺序二叉树转为链式二叉树，bt->lchild =CreateBTree(str,2*i)， bt->rchild             =CreateBTree(str,2*i+1)。
    递归出口为   if(i>len-1 || i<=0) return NULL，if(str[i]==‘#‘) return NULL。

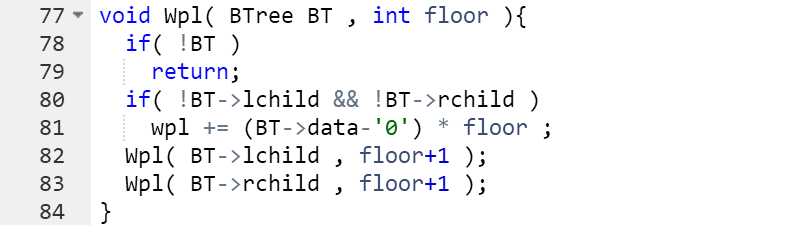
递归求WPL
    先设置一个全局变量wpl
    若BT==NULL，则返回空
    若BT为叶子节点，则累加wpl += (BT->data-‘0‘) * floor
    BT指向孩子节点时，floor就加1 
    所以递归Wpl(BT->lchild,floor+1)，Wpl(BT->rchild,floor+1);

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {

        if(!p || !q) return NULL;

        vector<TreeNode*> path1,path2;
        findPath(root,p,path1);
        findPath(root,q,path2);

        if(path1.empty() || path2.empty()) return NULL;

        int i = 0;
        while(i<path1.size() && i<path2.size() && path1[i]==path2[i]) i++;

        return path1[i-1];
}

bool findPath(TreeNode *root, TreeNode *p, vector<TreeNode*> &path){

        if(!root) return false;
        if(root==p) {
            path.push_back(p); 
            return true;
        }
        path.push_back(root);
        bool flag1 = findPath(root->left,p,path);
        if(flag1) return true;
        bool flag2 = findPath(root->right,p,path);
        if(flag2) return true;

        path.pop_back();
        return false;
}