博客作业04--树

标签：raid   parent   compare   int   枚举   pareto   ati   出现   树根   

1.学习总结

1.1树结构思维导图

1.2 树结构学习体会

• 学习树结构一方面是对前面队列，栈综合的应用，另一方面是对后面图学习的铺垫
• 树这方面理解有点困难，尤其是一系列的递归，只有多做多想才能理解

2.PTA实验作业

2.1 题目1：求二叉树高度

2.2 设计思路

• 定义变量 lchild,rchild

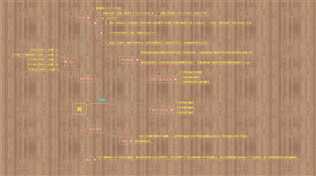
• 递归出口为b为空，递归条件为 lchildh=GetHeight(BT->Left);rchildh=GetHeight(BT->Right);
  返回最大值

  2.3 代码截图

  

  2.4 PTA提交列表说明。

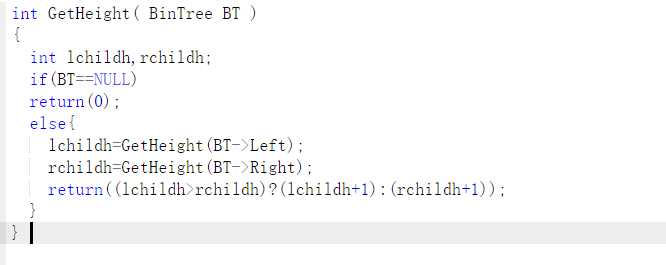
  没有问题

2. 1题目1：表达式树

2.2 设计思路

• 建op栈
• 初始化根节点栈

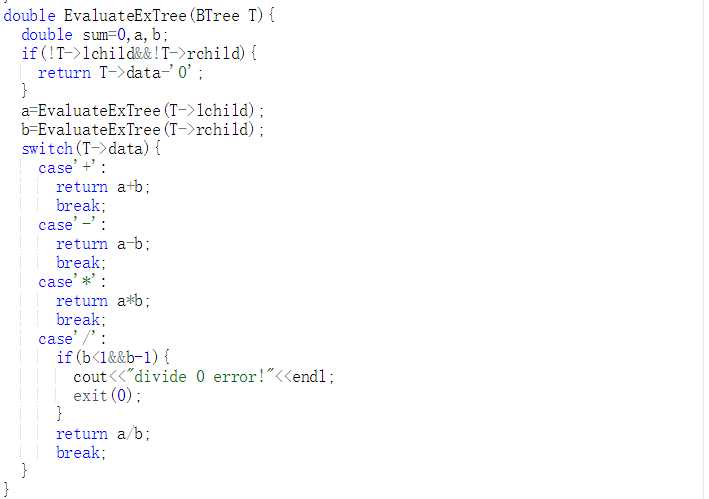
• while（表达式未结束）
  如果是操作数，生成一个只有根节点 的子树
  while大于栈顶运算符
  栈顶优先级高，则创建一个树节点，操作数的栈弹出2个，合成一个子树
  如果大于栈顶运算符，压栈
  如果等于栈顶运算符，出栈

  2.3 代码截图

  
  

2.4 PTA提交列表说明

2. 1题目1：还原二叉树

2.2 设计思路

• 如果n<0, 返回空，递归结束
• 创建根节点BT，BT->data=*pre

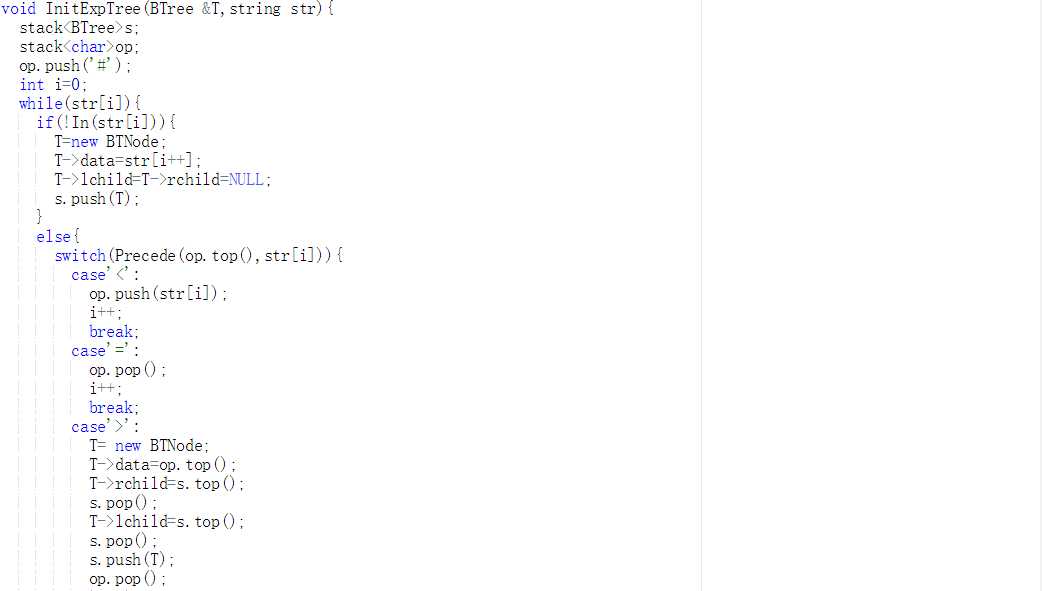
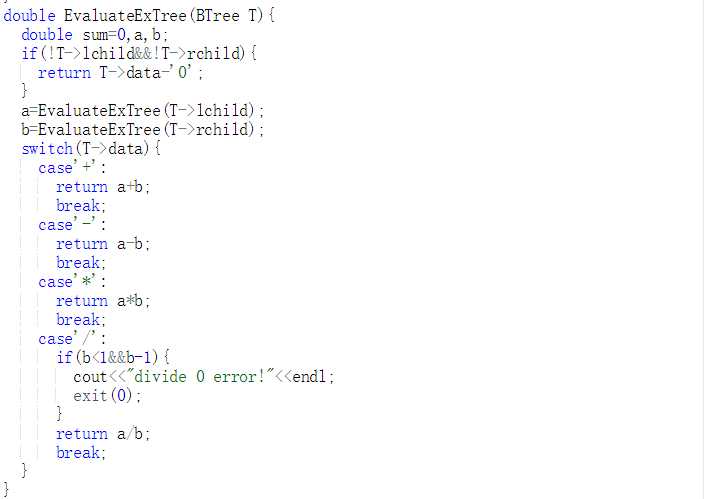
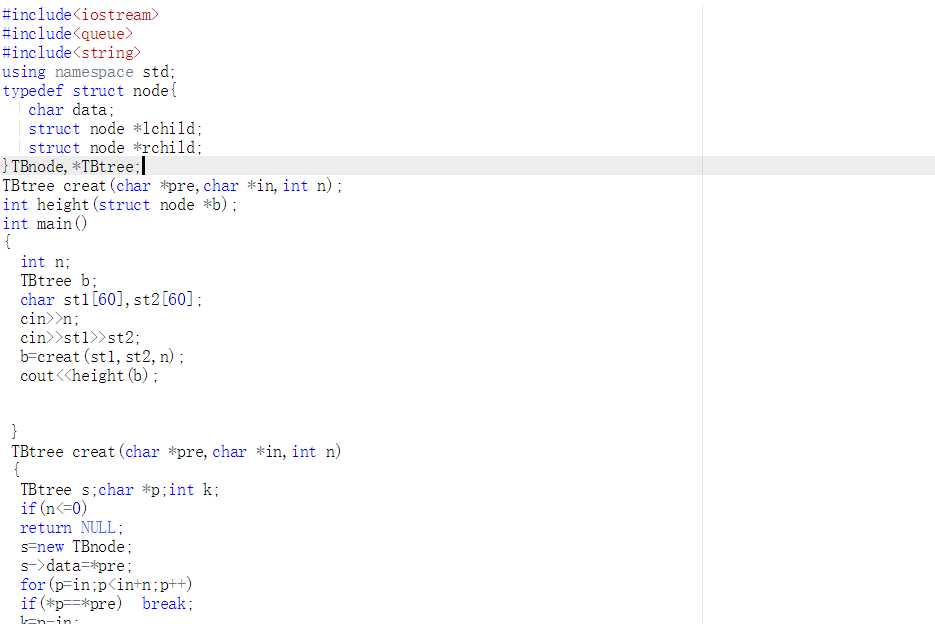
• 查找根节点在中序序列的位置k
  创建左子树 BT->lchild(pre+1,in,k)
  创建右子树 BT->rchild(pre+k+1,in+k+1,n-1-k)

  2.3 代码截图

  

2.4 PTA提交列表说明

• 没有问题

3.截图本周题目集的PTA最后排名

4. 阅读代码

/**平衡因子枚举类*/  
enum BalanceFactor{  
    LH("左子树高"),EH("左右等高"),RH("右子树高");  
      
    private String illustration="";  
      
    private BalanceFactor(String s){  
        this.illustration=s;  
    }  
      
    public String toString(){  
        return this.illustration;  
    }  
}  
/** 
 * 平衡二叉树结点 
 */  
class AVLNode<E extends Comparable<E>>{  
    /**结点关键字*/  
    E key=null;  
    /**结点的平衡因子*/  
    BalanceFactor bFactor=BalanceFactor.EH;  
    /**结点的直接父亲*/  
    AVLNode<E> parent=null;  
    /**结点的左右孩子*/  
    AVLNode<E> lchild,rchild=null;  
      
    AVLNode(E k){  
        this.key=k;  
    }  
    /** 
     * 格式输出结点 
     */  
    public String toString(){  
        //String fomateStr="";  
        //if(this.lchild==null)  
        String lchildStr=(this.lchild==null)?"null":this.lchild.key.toString();  
        String rchildStr=(this.rchild==null)?"null":this.rchild.key.toString();  
        return this.key+"[lchild="+lchildStr+"，rchild="+rchildStr+"]";  
    }  
  
}  
/** 
 * 平衡二叉查找树 
 * @author heartraid 
 */  
public class AVL<E extends Comparable<E>> {  
  
    /**树根*/  
    private AVLNode<E> root=null;  
    /**当前树是否变高*/  
    public boolean isTaller=false;  
      
    public AVL(){  
    }  
      
      
    public boolean insert(E key){  
        System.out.print("插入["+key+"]：");  
        if(key==null) return false;  
        if(root==null){  
            System.out.println("插入到树根。");  
            root=new AVLNode<E>(key);  
            return true;  
        }  
        else{  
            System.out.print("搜索路径[");  
            return insertAVL(key,root);  
        }  
    }  
      
    private boolean insertAVL(E key,AVLNode<E> node){  
        System.out.print(node.key+" —>");  
        // 树中存在相同的key,不需要插入  
        if(node.key.compareTo(key)==0){  
            System.out.println("].  搜索有相同关键字，插入失败");  
            isTaller=false;  
            return false;  
        }  
        else{  
            //左子树搜索  
            if(node.key.compareTo(key)>0){  
                //当前node的左孩子为空,则插入到结点的做孩子并修改结点的平衡因子为LH  
                if(node.lchild==null){  
                    System.out.println("].  插入到"+node.key+"的左孩子");  
                    AVLNode<E> newNode=new AVLNode<E>(key);  
                    node.lchild=newNode; //设置左孩子结点  
                    newNode.parent=node; //设置父亲结点  
                    isTaller=true; //树长高了  
                }  
                //左孩子不为空，则继续搜索下去  
                else{  
                    insertAVL(key,node.lchild);  
                }  
                //当前如果树长高了，说明是因为左孩子的添加改变了平衡因子（左高）。  
                if(isTaller){  
                    System.out.print("          树变化了，"+node.key+"的平衡因子变化");  
                    switch(node.bFactor){  
                        //原来结点平衡因子是LH(bf=1)，则左高以后bf=2，因此需要做左平衡旋转  
                        case LH: {  
                            System.out.println("[LH=1 ——> LH=2]. 出现了不平衡现象[左比右高2]");  
                            System.out.println("          ★ 以"+node.key+"为根将树进行左平衡处理");  
                            leftBalance(node);  
                            isTaller=false;   
                            break;  
                        }  
                        //原来结点平衡因子是EH(bf=0),则左高了以后bf=1,不需要平衡处理。  
                        case EH:{  
                            System.out.println("[EH=0 ——> LH=1]. 没有不平衡现象");  
                            node.bFactor=BalanceFactor.LH;  
                            isTaller=true;  
                            break;  
                        }  
                        //原来结点平衡因子是RH(bf=-1)，则左高以后bf=0,不需要平衡处理。  
                        case RH:{  
                            System.out.println("[RH=-1 ——> EH=0]. 没有不平衡现象");  
                            node.bFactor=BalanceFactor.EH;  
                            isTaller=false;  
                            break;  
                        }  
                    }//end switch  
                }//end if  
            }//end if  
            //右子树搜索  
            else{  
                if(node.rchild==null){  
                    System.out.println("].  插入到"+node.key+"的右孩子");  
                    AVLNode<E> newNode=new AVLNode<E>(key);  
                    node.rchild=newNode; //设置右孩子结点  
                    newNode.parent=node; //设置父亲结点  
                    isTaller=true; //树长高了  
                }  
                else{  
                    insertAVL(key,node.rchild);  
                }  
                //当前如果树长高了，说明是因为右孩子的添加改变了平衡因子（右高）。  
                if(isTaller){  
                    System.out.print("          树变化了，"+node.key+"的平衡因子变化");  
                    switch(node.bFactor){  
                        //原来结点平衡因子是LH(bf=1)，则右高以后bf=0，不需要平衡处理。  
                        case LH: {  
                            System.out.println("[LH=1 ——> EH=0]. 没有不平衡现象");  
                            node.bFactor=BalanceFactor.EH;  
                            isTaller=false;  
                            break;  
                        }  
                        //原来结点平衡因子是EH(bf=0),则右高了以后bf=-1,不需要平衡处理。  
                        case EH:{  
                            System.out.println("[EH=0 ——> RH=-1]. 没有不平衡现象");  
                            node.bFactor=BalanceFactor.RH;  
                            isTaller=true;  
                            break;  
                        }  
                        //原来结点平衡因子是RH(bf=-1)，则右高以后bf=0,因此需要做右平衡旋转。  
                        case RH:{  
                            System.out.println("[RH=-1 ——> RH=-2]. 出现了不平衡现象[左比右矮2]");  
                            rightBalance(node);  
                            isTaller=false;   
                            break;  
                        }  
                    }//end switch  
                }//end if(isTaller)  
            }//end else  
            return true;  
        }//end else  
    }  
    /** 
     * 左平衡旋转处理 
     * 先对node的左子树进行单左旋处理，在对node树进行单右旋处理 
     *  
     *          100                   100                90 
         *     /  \        左旋       /  \     右旋     /  \ 
         *    80  120   ------>     90  120   ------> 80  100   
         *   / \                    /                /  \    \ 
         *  60 90                   80              60  85  120 
         *     /                   / \ 
         *    85                  60 85 
     *  
     * @param node 需要做处理的子树的根结点 
     */  
    private void leftBalance(AVLNode<E> node){  
        // node.parent指向新的孩子结点  
        AVLNode<E> lc=node.lchild;//lc指向node的左孩子结点  
        switch(lc.bFactor){  
            case LH:{  //新结点插入在node的左孩子的左子树上，则需要单右旋处理  
                System.out.println("           ┖ 对"+node.key+"进行单右旋转处理");  
                node.bFactor=lc.bFactor=BalanceFactor.EH;  
                rRotate(node);  
                break;  
            }  
            case RH:{  //新结点插入在node的左孩子的右子树上，需要双旋处理  
                System.out.println("            ┖ 对"+node.key+"的左子树进行单左旋转处理，再对其本身树进行单右循环处理");  
                AVLNode<E> rd=lc.rchild; //rd指向node左孩子的右子树根  
                switch(rd.bFactor){ //修改node与其左孩子的平衡因子  
                    case LH:{  
                        node.bFactor=BalanceFactor.RH;  
                        lc.bFactor=BalanceFactor.EH;  
                        break;  
                    }  
                    case EH:{  
                        node.bFactor=lc.bFactor=BalanceFactor.EH;  
                        break;  
                    }  
                    case RH:{  
                        node.bFactor=BalanceFactor.EH;  
                        lc.bFactor=BalanceFactor.LH;  
                        break;  
                    }  
                }//switch  
                rd.bFactor=BalanceFactor.EH;  
                lRotate(node.lchild);  
                rRotate(node);  
                break;  
            }  
        }  
          
    }  
    /** 
     * 右平衡旋转处理 
     *  
     *        80                         80                       85   
         *   /  \            右 旋      /  \        左 旋        /  \      
         *  60  100    ------>        60   85   ------->        80  100 
         *      /  \                        \                  /   /  \        
         *     85  120                      100               60  90  120 
         *      \                          /  \ 
         *      90                        90  120  
     *  
     * @param node 
     */  
    private void rightBalance(AVLNode<E> node){  
        AVLNode<E> lc=node.rchild;//lc指向node的右孩子结点  
        switch(lc.bFactor){  
            case RH:{  //新结点插入在node的右孩子的右子树上，则需要单左旋处理  
                node.bFactor=lc.bFactor=BalanceFactor.EH;  
                lRotate(node);  
                break;  
            }  
            case LH:{  //新结点插入在node的右孩子的左子树上，需要双旋处理  
                AVLNode<E> rd=lc.lchild; //rd指向node右孩子的左子树根  
                switch(rd.bFactor){ //修改node与其右孩子的平衡因子  
                    case LH:{  
                        node.bFactor=BalanceFactor.EH;  
                        lc.bFactor=BalanceFactor.RH;  
                        break;  
                    }  
                    case EH:{  
                        node.bFactor=lc.bFactor=BalanceFactor.EH;  
                        break;  
                    }  
                    case RH:{  
                        node.bFactor=BalanceFactor.LH;  
                        lc.bFactor=BalanceFactor.EH;  
                        break;    
                    }  
                }//switch  
                rd.bFactor=BalanceFactor.EH;  
                rRotate(node.rchild);  
                lRotate(node);  
                break;  
            }  
        }  
    }  
      
      
    /** 
     * 对以node为根的子树进行单右旋处理，处理后node.parent指向新的树根，即旋转之前 
     * node的左孩子结点 
     *      100<-node.parent                 80<-node.parent 
     *      /                               /  \ 
     *     80             ———>         60   100 
     *    /  \                                  / 
     *   60  85                                85 
     */  
    private void rRotate(AVLNode<E> node){  
          
        AVLNode<E> lc=node.lchild;//lc指向node的左孩子结点  
          
        node.lchild=lc.rchild;  
        lc.rchild=node;  
        if(node.parent==null){  
            root=lc;  
        }  
        else if(node.parent.lchild.key.compareTo(node.key)==0)  
            node.parent.lchild=lc;  
        else node.parent.rchild=lc;  
    }  
    /** 
     * 对以node为根的子树进行单左旋处理，处理后node.parent指向新的树根，即旋转之前 
     * node的右孩子结点 
     *      100<-node.parent                     110<-node.parent 
     *        \                                  /  \ 
     *        110        ————>             100  120 
     *        /  \                               \ 
     *      105  120                             105 
     */  
    private void lRotate(AVLNode<E> node){  
        AVLNode<E> rc=node.rchild;//lc指向node的右孩子结点  
        node.rchild=rc.lchild;  
        rc.lchild=node;  
        if(node.parent==null){  
            root=rc;  
              
        }  
        else if(node.parent.lchild.key.compareTo(node.key)==0)  
                node.parent.lchild=rc;  
        else node.parent.rchild=rc;  
    }  
      
    /** 
     * 得到BST根节点 
     * @return BST根节点f 
     */  
    public AVLNode<E> getRoot(){  
        return this.root;  
    }  
   
    /** 
     * 递归前序遍历树 
     */  
    public void preOrderTraverse(AVLNode<E> node){  
        if(node!=null){  
            System.out.println(node);  
            preOrderTraverse(node.lchild);  
            preOrderTraverse(node.rchild);  
        }  
    }  
    /** 
     * 测试 
     * @param args 
     */  
    public static void main(String[] args) {  
        AVL<Integer> avl=new AVL<Integer>();  
        avl.insert(new Integer(80));  
        avl.insert(new Integer(60));  
        avl.insert(new Integer(90));  
        avl.insert(new Integer(85));  
        avl.insert(new Integer(120));  
        avl.insert(new Integer(100));  
      
        System.out.println("前序遍历AVL：");  
        avl.preOrderTraverse(avl.getRoot());  
  
    }  
} 

• 平衡二叉树的优势在于不会出现普通二叉查找树的最差情况。其查找的时间复杂度为O(logN)

• 地址：https://blog.csdn.net/sagadean/article/details/7081625

  5. 代码Git提交记录截图

  

博客作业04--树

标签：raid   parent   compare   int   枚举   pareto   ati   出现   树根   

原文地址：https://www.cnblogs.com/guobaoqing/p/8994661.html