博客作业04--树

标签：创建   需要   3.1   erro   列表   定义   exp   作业   bool   

1.学习总结

1.1树结构思维导图

1.2树结构学习体会

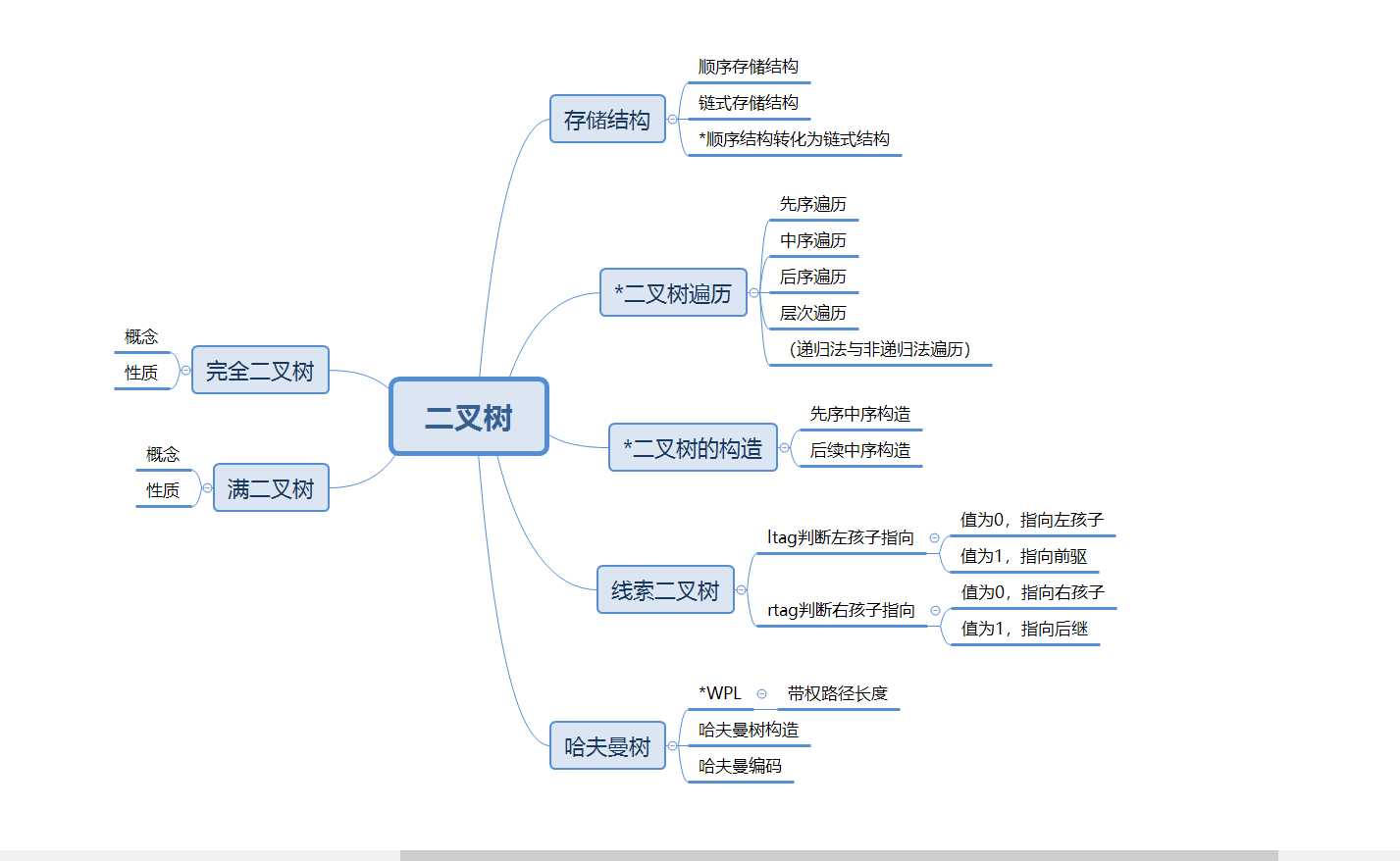
对于这两周的树的学习，与之前的知识相比，能感觉到难度明显加大，刚开始不会的时候感觉很复杂，学会以后代码无论是简洁程度还是效率上都高了很多。对于本节知识的学习，我觉得需要一定的想象能力，特别是有递归函数时，对函数的出口和递归部分的设计非常有意思。做题过程中，多结合图形更方便理解，也容易记忆。

2.PTA实验作业

题目1：二叉树层次遍历

设计思路

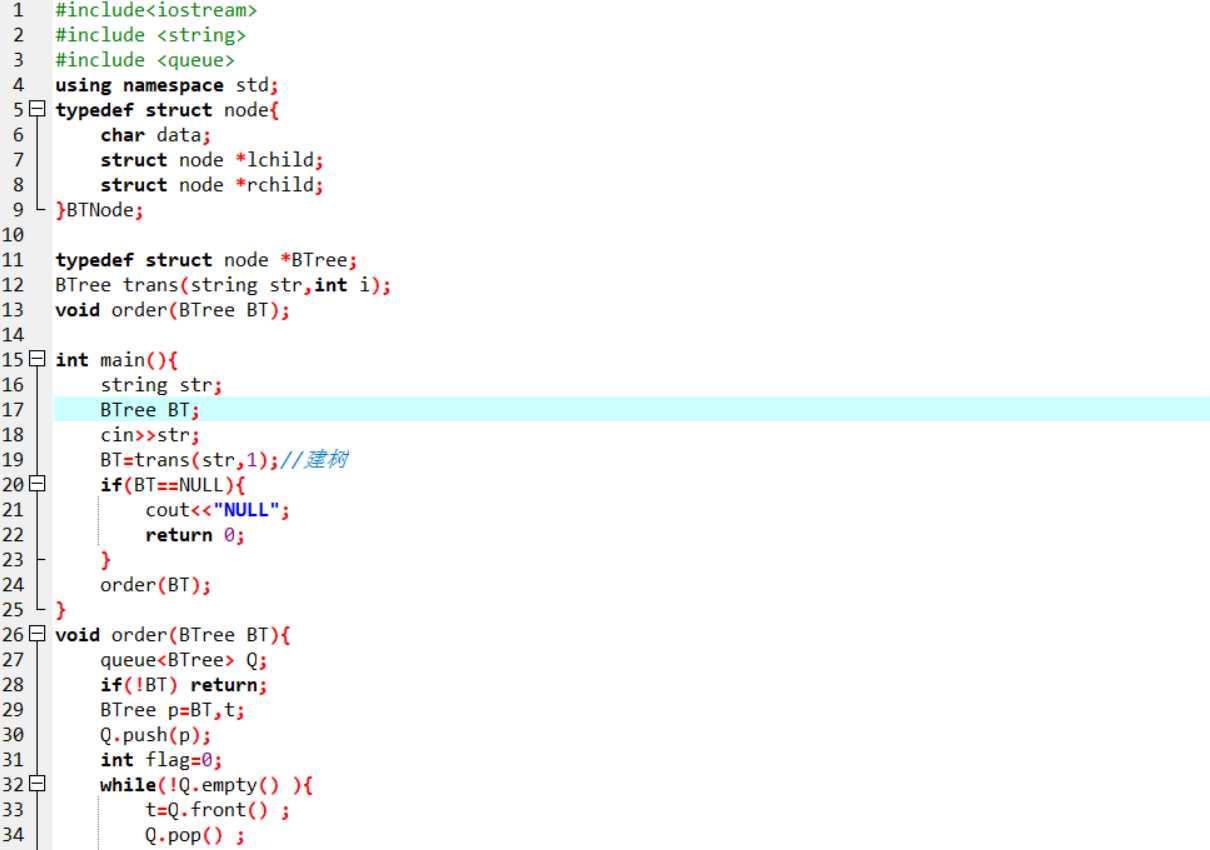
定义sting str,BTree BT;
输入str
根据str建树BT=trans(str,1);
若树为空，输出NULL，结束程序
层次遍历order(BT) 

BTree trans(string str,int i){ //递归建树 
      判断i是否大于str.size()-1,否则返回NULL；
      判断str[i]是否为‘#‘，否则返还NULL；
      BTree B申请空间；
      存入数据B->data=str[i];
      求左子树B->lchild=trans(str,2*i);
      求右子树 B->rchild=trans(str,2*i+1)
      return B 
} 
void order(BTree BT){
     若树为空，返回 
     创建队列Q  
     入队根节点
     while(队列不为空){
        访问队首
        输出队首节点的data;
        队首节点出队；
        若队首节点左子树不为空，则入队
        若队首节点右子树不为空，则入队 
     } 
}

代码截图

PTA提交列表说明

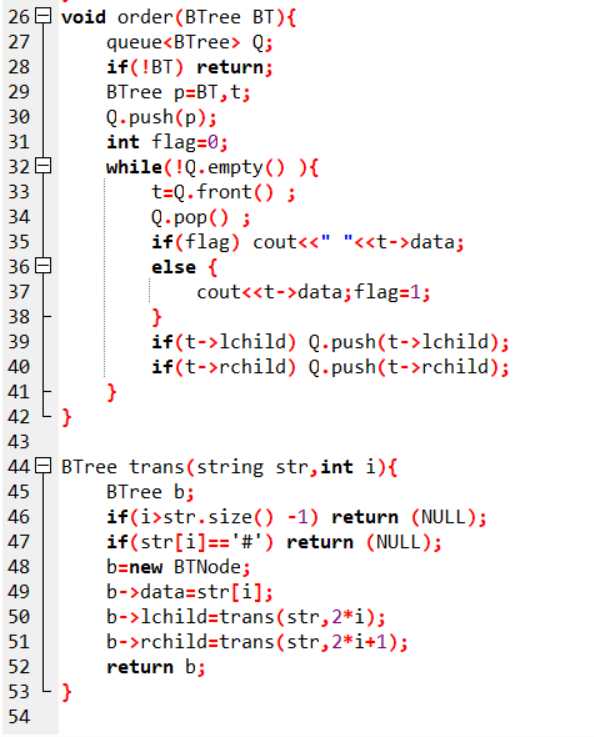
说明：树为空时没有输出NULL，导致部分正确

题目2：二叉树叶子结点带权路径长度和

设计思路

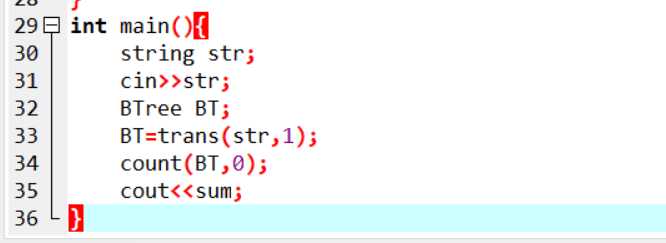
定义全局变量sum=0；
main（）
{ 
定义sting str,BTree BT;
输入str
根据str建树BT=trans(str,1);
计算WPL(BT,0) 
输出sum 
}
 
BTree trans(string str,int i){ //递归建树 
      判断i是否大于str.size()-1,否则返回NULL；
      判断str[i]是否为‘#‘，否则返还NULL；
      BTree B申请空间；
      存入数据B->data=str[i];
      求左子树B->lchild=trans(str,2*i);
      求右子树 B->rchild=trans(str,2*i+1)
      return B 
} 
void WPL( BTree BT ,int n){ //计算WPL
     if BT不为空{
        递归遍历左子树，同时参数n+1,WPL(BT->lchild,n+1) 
        if BT左右子树都为空
           sum+=BT->data*n; 
        递归遍历右子树，同时参数n+1,WPL(BT->lchild,n+1) 
     } 
} 

代码截图

PTA提交列表说明

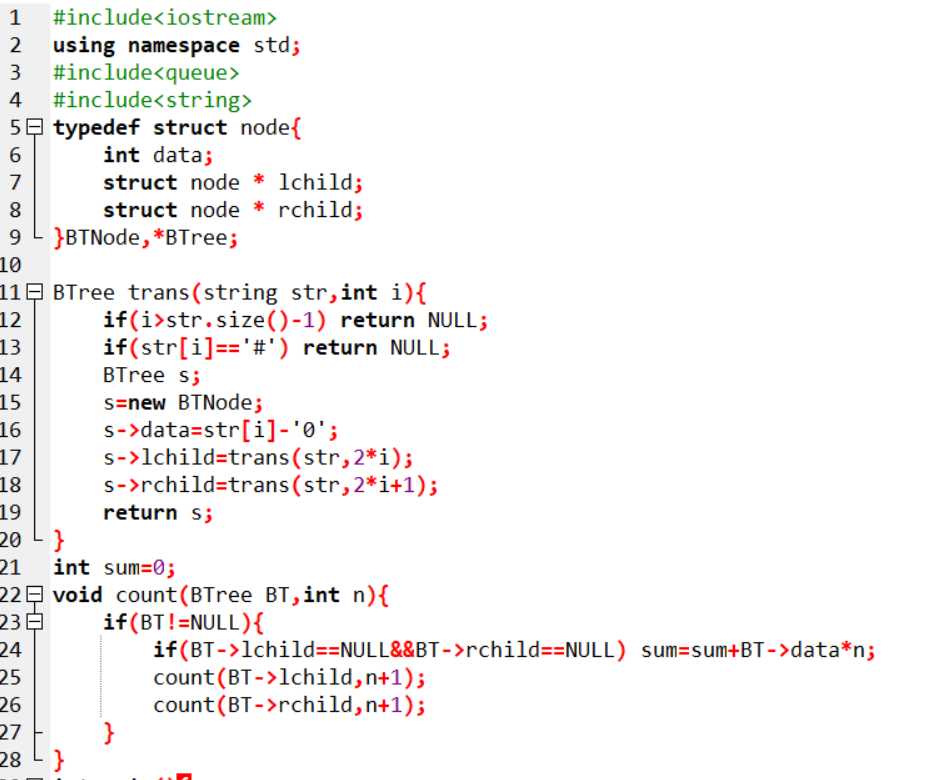
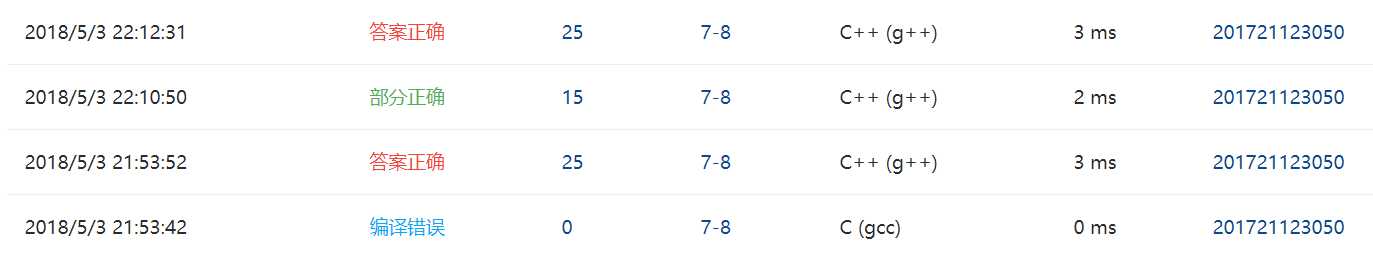
说明：本题的部分正确是因为，用递归方法建树时出错，导致答案错误

题目3：表达式树

设计思路

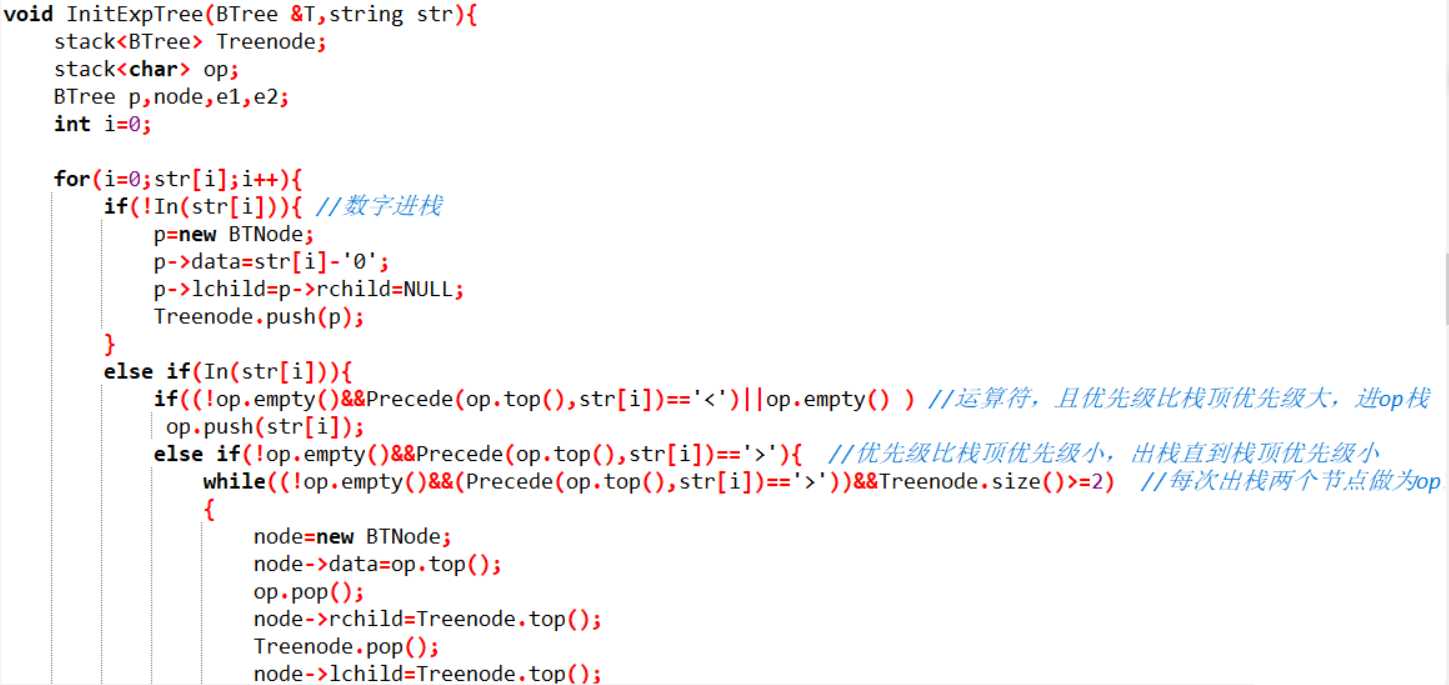
void InitExpTree(BTree &T,string str){ 
    创建两个栈，op存放运算符，Treenode存放树节点
    for i=0 to str[i]
    {
        if(str[i]为数字 ) 存进Treenode栈
        else{
             if(str[i]优先级大于op栈顶运算符||op栈为空) str[i]进op 栈
             else if (str [i]优先级小于op栈顶运算符) {
                  while(str [i]优先级小于op栈顶运算符&&Treenode栈元素大等于2){
                      出栈op栈顶元素做根节点，出栈Treenode栈两个元素做其左右孩子
                         根节点进Treenode栈 
                   }
                   if(op栈不空&&栈顶为‘(‘) 出栈
                   if(str[i]!=‘)‘) 进栈 
             } 
        } 
     }
     while(op栈不空&&Treenode栈元素大等于2) { 
        出栈op栈顶元素做根节点，出栈Treenode栈两个元素做其左右孩子
        根节点进Treenode栈 
     } 
     T=Treenode栈顶 
 } 
 double EvaluateExTree(BTree T){
        if(T不为空){
             if(T->data为运算符){
                switch(T->data ) //判断运算符，递归运算 
                {
                   case‘+‘:return(EvaluateExTree(T->lchild)+EvaluateExTree(T->rchild));break;
                   case‘-‘:return(EvaluateExTree(T->lchild)-EvaluateExTree(T->rchild));break;
                   case‘*‘:return(EvaluateExTree(T->lchild)*EvaluateExTree(T->rchild));break;
                   case‘/‘:if(EvaluateExTree(T->rchild)!=0) {return(EvaluateExTree(T->lchild)/EvaluateExTree(T->rchild));break;} 
                         else {
                            cout<<"divide 0 error!";exit (0);
                         }
                } 
             } 
         
         } 
 } 

代码截图

PTA提交列表说明

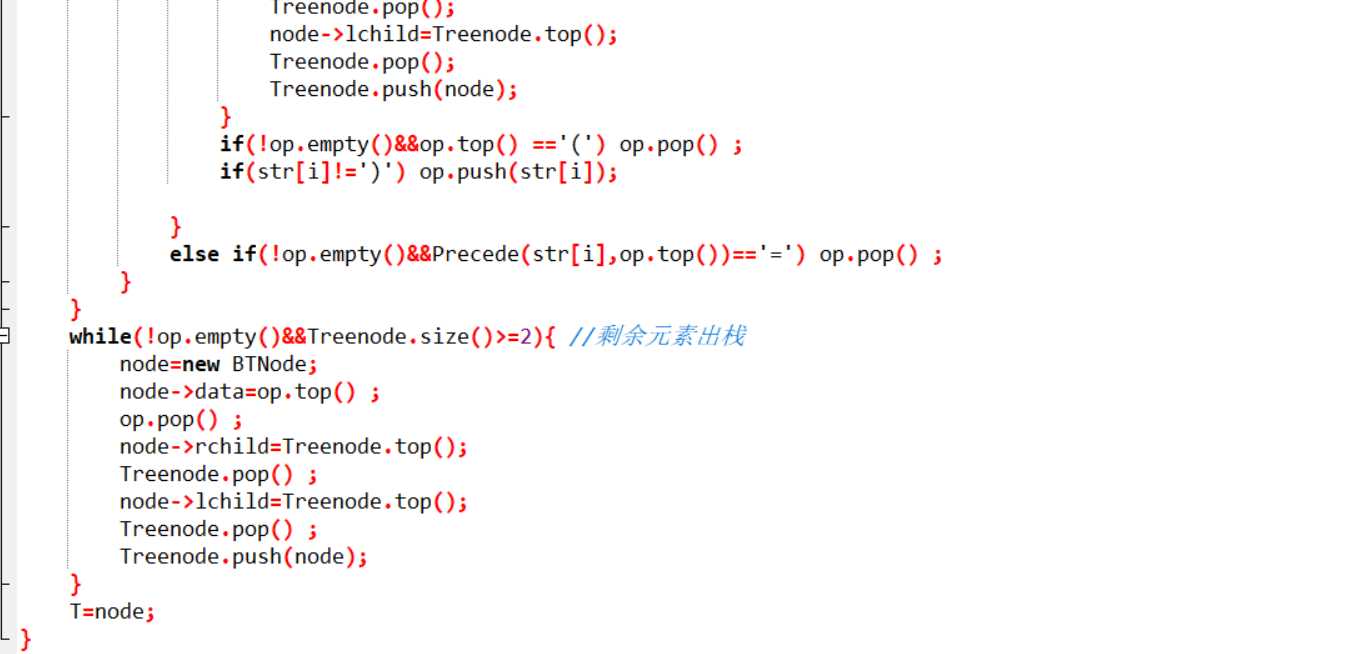
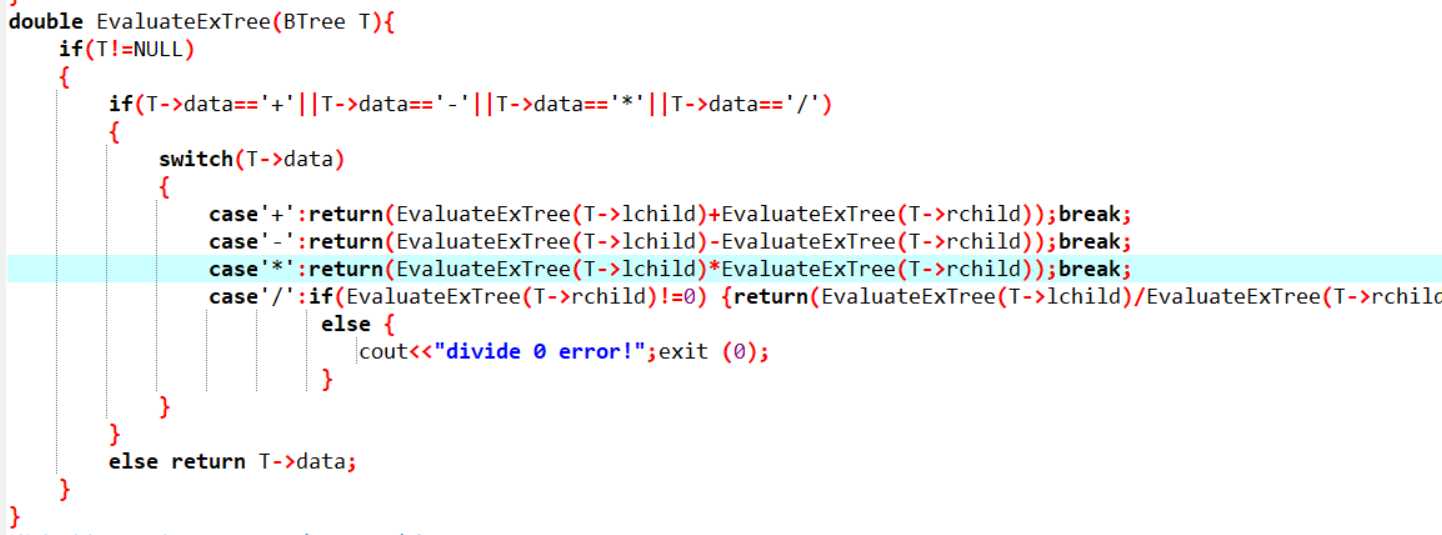
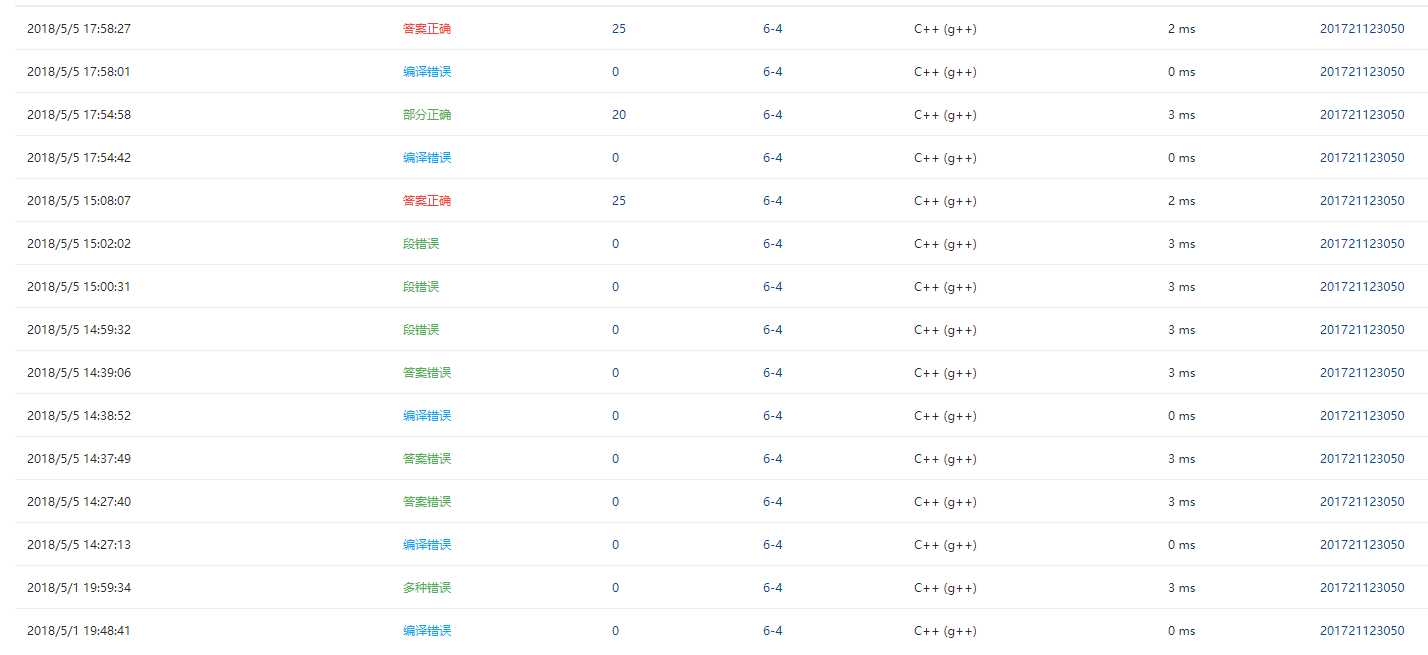
说明：建树时对OP栈的优先级中，对右括号判断完后的处理出现问题。

3.截图本周题目集的PTA最后排名

本次题目集总分：230

3.1 PTA排名

3.2 我的得分：2

4. 阅读代码

题目：天平

输入一个树状天平，根据力矩相等原则判断是否平衡。如图6-5所示，所谓力矩相等，就是WlDl=WrDr，其中Wl和Wr分别为左右两边砝码的重量，D为距离。采用递归（先序）方式输入：每个天平的格式为W1，D1，W2，D2，当W1或W2为0时，表示该“砝码”实际是一个子天平，接下来会描述这个子天平。当W1=W2=0时，会先描述左子天平，然后是右子天平。

样例输入：

1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2
其正确输出为YES

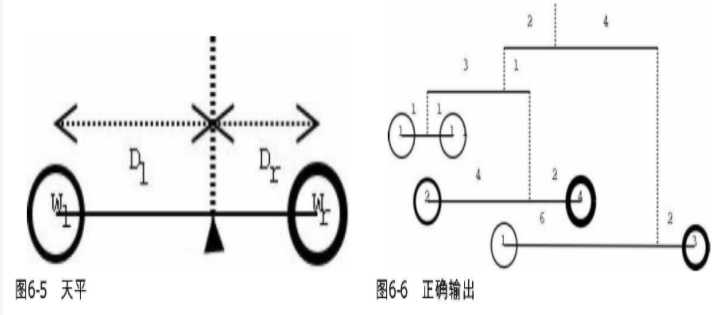
代码：

#include<iostream>
using namespace std;
//输入一个子天平，返回子天平是否平衡，参数W修改为子天平的总重量
bool solve(int &W){
    int W1,D1,W2,D2;
    bool b1=true,b2=true;
    cin>>W1>>D1>>W2>>D2;
    if(!W1) b1=solve(W1); //如果有子天平就递归下去
    if(!W2) b2=solve(W2); //如果有子天平就递归下去
    W=W1+W2;
    return b1&&b2&&(W1*D1==W2*D2); /*这里的&&顺便返回了上一步的正确与否的状态，所以只要一步是false，所有返回就都为false*/
} 

int main(){
    int T,W;
    cin>>T;
    while(T--){
        if(solve(W)) cout<<"yes\n"; else cout<<"No\n";
        if(T) cout<<"/n";
    }
    return 0;
}

来源：算法入门书上看到的

5. 代码Git提交记录截图

博客作业04--树

标签：创建   需要   3.1   erro   列表   定义   exp   作业   bool   

原文地址：https://www.cnblogs.com/xzjj/p/8995241.html