标签：ber   art   bsp   格式   另一个   code   哈夫曼   思维导图   最小   

1.学习总结

1.1树结构思维导图

使用思维导图将树结构的知识点串在一起。树中的每个知识点需细化到每个操作如何实现。

1.2 树结构学习体会

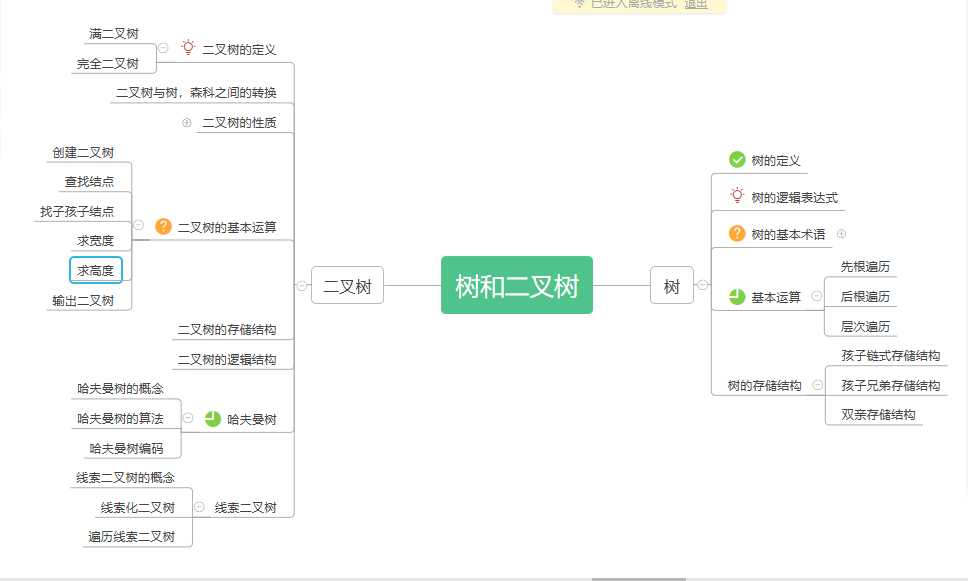
1，感觉树很有趣，但有时自己会犯迷糊，自己的想象能力不足

2，多结合图型更方便理解，也更容易记忆

3，多在草稿纸上画图，这样能够帮助理解

4，在二叉树的函数中，还不清楚如何递归计算的机理

2.PTA实验作业

具体书写内容及格式如下：

2.1 题目1：6-4 jmu-ds-表达式树

2.2 设计思路（伪代码或流程图）

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明。

3.1   jmu-ds-二叉树操作

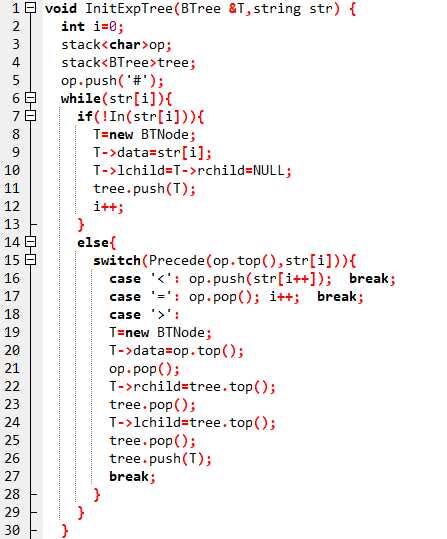
1，设计思路

  2，源代码：

 

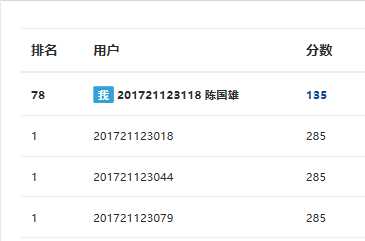
3，提交列表

说明：

 

 

3.截图本周题目集的PTA最后排名

本次题目集总分：285分
必做题共：230分

3.1 PTA排名截图

3.2 我的总分：1.5

本题评分规则：

 （1）2个题目集PTA总分285分：3分（全部题目都做）
 （2）PTA总分在230分--340分：2.5分（必做题全部做完，选做题做部分）
 （3）PTA总分在180--230分：2分（必做题大部分做完）
 （4）PTA总分在130--180分：1.5分
 （5）PTA总分在105分-130分：1分  
 （6）PTA总分在105分以下：0分     

4. 阅读代码（必做）

本次为必做

1，

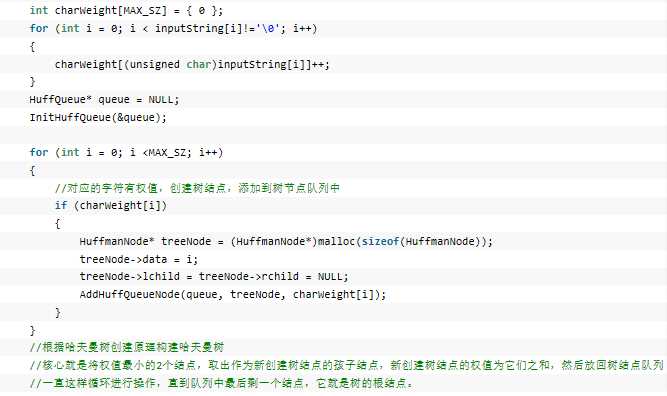
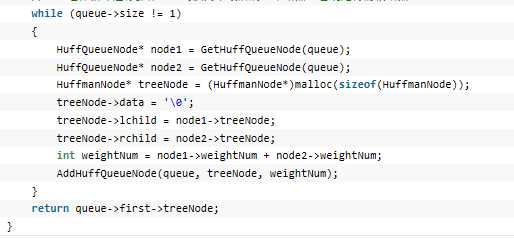
哈夫曼大叔说，从树中一个结点到另一个结点之间的分支构成2个结点之间的路径，路劲上的分支数目称作路径长度。树的路径长度就是从树根到每一结点的路径长度之和。如果考虑到带权的结点，结点的带权的路径长度就为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。

假设有n个权值{W1,W2.....,Wn}，构造一棵n个叶子结点的二叉树，每个叶子结点带权Wk，每个叶子的路径长度为1k，我们通常记作，其中带权路径长度WPL最小的二叉树称为哈夫曼树（又称最优二叉树）。

2，https://blog.csdn.net/qq_29542611/article/details/79334308 

五，代码Git提交记录截图

树与二叉树

标签：ber   art   bsp   格式   另一个   code   哈夫曼   思维导图   最小   

原文地址：https://www.cnblogs.com/chenguoxiong/p/8996188.html