标签:style blog http color io os ar strong for
皮尔森相关系数(Pearson correlation coefficient)也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ,是一种线性相关系数。皮尔森相关系数是用来反映两个变量线性相关程度的统计量,用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1。相关系数用r表示,其中n为样本量,分别为两个变量的观测值和均值。r描述的是两个变量间线性相关强弱的程度。r的绝对值越大表明相关性越强。之间
| 相关性 | 负 | 正 |
|---|---|---|
| 无 | ?0.09 to 0.0 | 0.0 to 0.09 |
| 弱 | ?0.3 to ?0.1 | 0.1 to 0.3 |
| 中 | ?0.5 to ?0.3 | 0.3 to 0.5 |
| 强 | ?1.0 to ?0.5 | 0.5 to 1.0 |
皮尔森相关系数计算公式如下:
分子是协方差,分子是两个变量标准差的乘积,X和Y的标准差都不为0。
由于μX = E(X), σX2 = E[(X ? E(X))2] = E(X2) ? E2(X),Y也类似, 并且

故相关系数也可以表示成
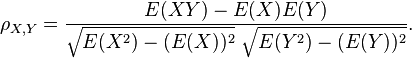
对于样本皮尔逊相关系数:
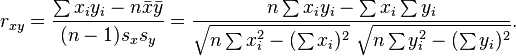
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:

以上方程定义了总体相关系数, 一般表示成希腊字母ρ(rho)。基于样本对协方差和标准差进行估计,可以得到样本相关系数, 一般表示成r:
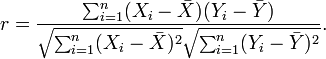
> read.csv("H:/docs/机器学习第2版/src/ABCgoods.csv")->mygoods
> mygoods
A原料 B原料 C原料 商品销量
1 0.85 0.12 0.30 4500
2 0.33 0.23 0.44 1800
3 0.64 0.24 0.12 3900
4 0.38 0.12 0.50 1000
5 0.10 0.20 0.88 740
6 0.28 0.17 0.55 990
7 0.15 0.80 0.77 910
8 0.18 0.70 0.75 930
> cov(mygoods)->myanalysis.cov
> myanalysis.cov
A原料 B原料 C原料 商品销量
A原料 0.06716964 -0.03539643 -0.05832321 368.2161
B原料 -0.03539643 0.07230714 0.03521786 -151.1464
C原料 -0.05832321 0.03521786 0.06546964 -321.9196
商品销量 368.21607143 -151.14642857 -321.91964286 2235941.0714
> cor(mygoods)->myanalysis.cor
> myanalysis.cor
A原料 B原料 C原料 商品销量
A原料 1.0000000 -0.5079048 -0.8794982 0.9501366
B原料 -0.5079048 1.0000000 0.5118614 -0.3759041
C原料 -0.8794982 0.5118614 1.0000000 -0.8413899
商品销量 0.9501366 -0.3759041 -0.8413899 1.0000000
> cor.test(~A原料+B原料,data=mygoods)
Pearson‘s product-moment correlation
data: A原料 and B原料
t = -1.4443, df = 6, p-value = 0.1988
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8929757 0.3064479
sample estimates:
cor
-0.5079048
> cor.test(~A原料+商品销量,data=mygoods)
Pearson‘s product-moment correlation
data: A原料 and 商品销量
t = 7.4634, df = 6, p-value = 0.0002985
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7427838 0.9911796
sample estimates:
cor
0.9501366
> cor.test(~C原料+商品销量,data=mygoods)
Pearson‘s product-moment correlation
data: C原料 and 商品销量
t = -3.8136, df = 6, p-value = 0.008826
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9705934 -0.3358354
sample estimates:
cor
-0.8413899
> cor.test(~B原料+商品销量,data=mygoods)
Pearson‘s product-moment correlation
data: B原料 and 商品销量
t = -0.9936, df = 6, p-value = 0.3588
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8542858 0.4472372
sample estimates:
cor
-0.3759041
C原料、A原料分别与商品销量线性相关
A原料与B原料线性无关,应属于不需要按指定配比配置的。
标签:style blog http color io os ar strong for
原文地址:http://blog.csdn.net/myhaspl/article/details/39555063