标签:name 分享图片 a* 密码学 clu 技术分享 去空格 手工 mat
设多表代换密码中:
\[
A=\begin{bmatrix}
{3} & {13}&{21}&{9} \ {15}&{10}&{6}&{25}\ {10}&{17}&{4}&{8}\{1}&{23}&{7}&{2}
\end{bmatrix}
,
B=\begin{bmatrix}
{1}\\{21}\\{8}\\{17}
\end{bmatrix}
\]
加密为:\(C_i≡A{M_i}+\textbf{B}(mod\ 26)\)
对明文PLEASE SEND ME THE BOOK, MY CREDIT CARD NO IS SIX ONE TWO ONE THREE EIGHT SIX ZERO ONE SIX EIGHT FOUR NINE SEVEN ZERO TWO,
用解密变换
\(M_i≡A^{-1}(C_i-\textbf{B})(mod\ 26)\)
验证你的结果,其中
\[
A^{-1}=\begin{bmatrix}
{26} & {13}&{20}&{5} \ {0}&{10}&{11}&{0}\ {9}&{11}&{15}&{22}\{9}&{22}&{6}&{25}
\end{bmatrix}
\]
例 1.4.2 的简单验证:
#include<bits/stdc++.h>
#define rap(a,b) for(int a=0;a<b;++a)
using namespace std;
string encypt(string m,double a[][3],double b[]){
string ans;
for (int i=0;i<3;++i){
int tmp=0;
for (int j=0;j<3;++j){
tmp+=a[i][j]*(m[j]-'A');
}
tmp+=b[i];tmp%=26;
ans+=tmp+'A';
}
return ans;
}
string decypt(string c,double a[][3],double b[]){
string ans;
for(int i=0;i<3;++i){
int tmp=0;
for(int j=0;j<3;++j){
tmp+=a[i][j]*(c[j]-'A'-b[j]);
}
ans+=tmp%26+'A';
}
return ans;
}
int main(){
double a[3][3]={
11,2,19,
5,23,25,
20,7,17
};
double b[3]={0,0,0};
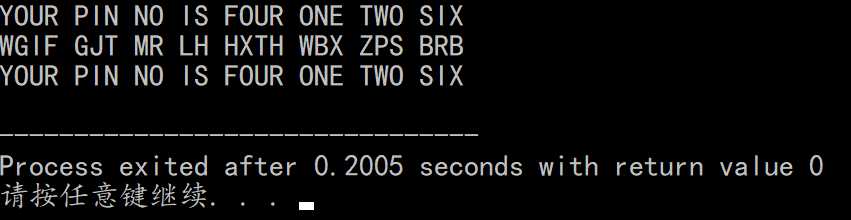
string c="YOUR PIN NO IS FOUR ONE TWO SIX";
//记录空格位置并去空格
vector<int>pos;
int tmp=c.find(' ');
while(tmp!=-1)
{
pos.push_back(tmp);
c.erase(tmp,1);
tmp=c.find(' ');
}
int i=0;
string m;
while(i!=c.size()){
m+=encypt(c.substr(i,3),a,b);
i+=3;
}
double a2[3][3]={
10,23,7,
15,9,22,
5,9,21
};
i=0;
string c2;
while(i!=m.size()){
c2+=decypt(m.substr(i,3),a2,b);
i+=3;
}
for(i=pos.size()-1;i>=0;--i)c.insert(pos[i]," ");
for(i=pos.size()-1;i>=0;--i)m.insert(pos[i]," ");
for(i=pos.size()-1;i>=0;--i)c2.insert(pos[i]," ");
cout<<c<<endl;
cout<<m<<endl;
cout<<c2<<endl;
return 0;
}
仿照例题,很容易得出习题 1.3 的算法实现:
#include<bits/stdc++.h>
#define rap(a,b) for(int a=0;a<b;++a)
using namespace std;
string encypt(string m,double a[][4],double b[]){
string ans;
for (int i=0;i<4;++i){
int tmp=0;
for (int j=0;j<4;++j){
tmp+=a[i][j]*(m[j]-'A');
}
tmp+=b[i];
ans+=tmp%26+'A';
}
return ans;
}
string decypt(string c,double a[][4],double b[]){
string ans;
int cc[4];
for(int i=0;i<4;++i)cc[i]=(int)(c[i]-'A'-b[i]+26)%26;
for(int i=0;i<4;++i){
int tmp=0;
for(int j=0;j<4;++j){
tmp+=a[i][j]*cc[j];
}
ans+=tmp%26+'A';
}
return ans;
}
int main(){
double a[4][4]={
3,13,21,9,
15,10,6,25,
10,17,4,8,
1,23,7,2
};
double b[4]={1,21,8,17};
string c="PLEASE SEND ME THE BOOK, MY CREDIT CARD NO IS SIX ONE TWO ONE THREE EIGHT SIX ZERO ONE SIX EIGHT FOUR NINE SEVEN ZERO TWO";
//记录空格位置并去空格
vector<int>pos;
int tmp=c.find(' ');
while(tmp!=-1)
{
pos.push_back(tmp);
c.erase(tmp,1);
tmp=c.find(' ');
}
//加密
int i=0;
string m;
while(i!=c.size()){
m+=encypt(c.substr(i,4),a,b);
i+=4;
}
//解密
double a2[4][4]={
26,13,20,5,
0,10,11,0,
9,11,15,22,
9,22,6,25
};
string c2;
i=0;
while(i!=m.size()){
c2+=decypt(m.substr(i,4),a2,b);
i+=4;
}
//还原空格
for(i=pos.size()-1;i>=0;--i)c.insert(pos[i]," ");
for(i=pos.size()-1;i>=0;--i)m.insert(pos[i]," ");
for(i=pos.size()-1;i>=0;--i)c2.insert(pos[i]," ");
cout<<c<<endl;
cout<<m<<endl;
cout<<c2<<endl;
return 0;
}

感谢现代密码学编者让我浪费的两小时。
首先求出
\[
C=\begin{bmatrix}
{3}\\{14}\\{13}\\{19}
\end{bmatrix},
M=\begin{bmatrix}
{4}\\{11}\\{13}\\{8}
\end{bmatrix}
\]
设
\[
A=\begin{bmatrix}
{a}&{b}\\{c}&{d}
\end{bmatrix}有
\begin{bmatrix}
{3}\\{14}
\end{bmatrix}*
\begin{bmatrix}
{a}&{b}\\{c}&{d}
\end{bmatrix}=\begin{bmatrix}
{4}\\{11}
\end{bmatrix},
\begin{bmatrix}
{13}\\{19}
\end{bmatrix}*
\begin{bmatrix}
{a}&{b}\\{c}&{d}
\end{bmatrix}=\begin{bmatrix}
{4}\\{11}
\end{bmatrix}
\]
可得
\[
\begin{cases}
{3*a+14*b≡4(mod\ 26)} &{①}\{3*c+14*d≡11(mod\ 26)}&{②}\{13*a+19*b≡13(mod\ 26)}&{③}\{13*c+19*d≡8(mod\ 26)}&{④}
\end{cases}
\]
联立解得
\[
A=\begin{bmatrix}
{10}&{13}\\{9}&{23}
\end{bmatrix}
\]
标签:name 分享图片 a* 密码学 clu 技术分享 去空格 手工 mat
原文地址:https://www.cnblogs.com/shy-/p/9011396.html