标签:根据 end 转移 解法 isp alc closed 初始 char
国际惯例的题面: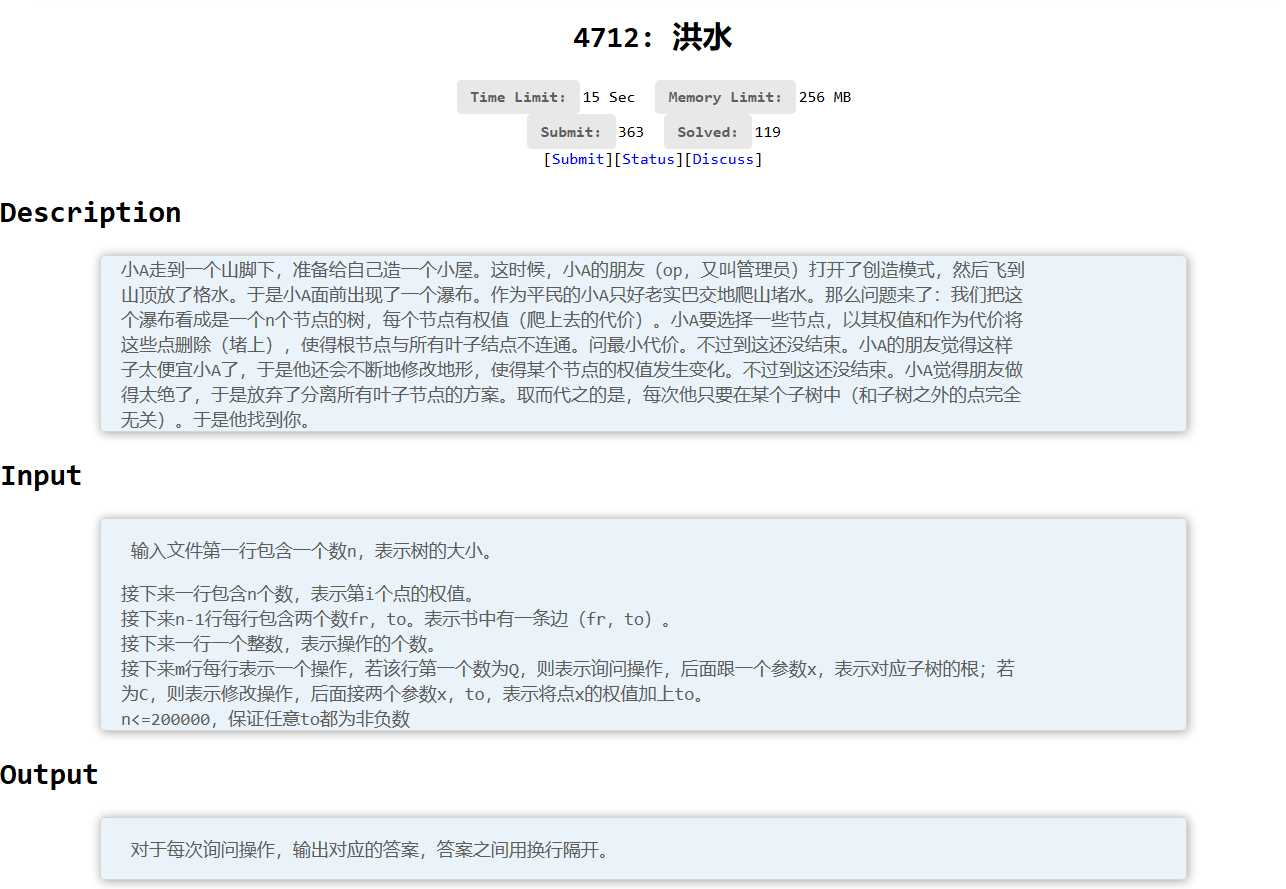
看起来很神的样子......如果我说这是动态DP的板子题你敢信?
基于链分治的动态DP?说人话,就是树链剖分线段树维护DP。
既然是DP,那就先得有转移方程。
我们令f[i]表示让i子树中的叶子节点全部与根不联通,所需要的最小代价,v[i]为输入的点权。
显然f[i]=min(v[i],sigma(f[soni])),边界条件是,如果i是叶子节点,则f[i]=v[i]。
我们需要用链分治去维护这个DP,所以要把DP拆成重链和轻链独立的形式。
我们还是用f[i]表示让i子树中的叶子节点全部与根不联通,所需要的最小代价,h[i]表示i的轻儿子的f值之和。
根据定义,h[i]=sigma(h[light_sons_i]),
同时我们有:f[i]=min(v[i],f[heavy_son_i]+h[i])。
这个转移我们能写成一个最短路矩阵相乘的形式:
{0,f[heavy_son_i]}*{{0,v[i]},{inf,h[i]}} = {0,f[i]}
(我的写法和C++多维数组的表示方法相同,inf表示不能转移)
显然(陈俊锟说过)这个矩阵连乘是具有结合性的,所以我们能用线段树维护一条链上转移矩阵的连乘积。
于是修改的时候,我们只需要从这个点一路改上去,在跳轻边的时候修改其父亲的h值和转移矩阵,然后线段树更新即可。
查询的话就查询这个点到其所在重链底端线段树上转移矩阵的连乘积,然后左乘一个初始化矩阵即可。
时间复杂度O(8nlog^2n),加上fread快读还是不慢(能看)的。
(其实分析题目性质能够让转移复杂度更低,然而不如矩阵的方法通用(反正就是个常数,不管他了)。关于分析性质的解法,见我BZOJ5210的题解)
代码:

1 #pragma GCC optimize(2) 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cctype> 6 typedef long long int lli; 7 const int maxn=2e5+1e2; 8 const lli inf=0x3f3f3f3f3f3f3f3fll; 9 10 struct Matrix { 11 lli dat[2][2]; 12 Matrix() { memset(dat,0x3f,sizeof(dat)); } 13 lli* operator [] (const int &x) { return dat[x]; } 14 const lli* operator [] (const int &x) const { return dat[x]; } 15 friend Matrix operator * (const Matrix &a,const Matrix &b) { 16 Matrix ret; 17 for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int k=0;k<2;k++) ret[i][j] = std::min( ret[i][j] , a[i][k] + b[k][j] ); 18 return ret; 19 } 20 }trans[maxn],ini; 21 22 lli v[maxn],f[maxn],h[maxn]; 23 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 24 int fa[maxn],siz[maxn],dep[maxn],son[maxn],top[maxn],id[maxn],rec[maxn],mxd[maxn],iid; 25 int n; 26 27 struct SegmentTree { 28 Matrix dat[maxn<<2]; 29 #define lson(pos) (pos<<1) 30 #define rson(pos) (pos<<1|1) 31 inline void build(int pos,int l,int r) { // Warning :: from right to left . 32 if( l == r ) return void(dat[pos]=trans[rec[l]]); 33 const int mid = ( l + r ) >> 1; 34 build(lson(pos),l,mid) , build(rson(pos),mid+1,r) , dat[pos] = dat[rson(pos)] * dat[lson(pos)]; 35 } 36 inline void update(int pos,int l,int r,const int &tar) { 37 if( l == r ) return void(dat[pos]=trans[rec[l]]); 38 const int mid = ( l + r ) >> 1; 39 tar <= mid ? update(lson(pos),l,mid,tar) : update(rson(pos),mid+1,r,tar); 40 dat[pos] = dat[rson(pos)] * dat[lson(pos)]; 41 } 42 inline Matrix query(int pos,int l,int r,const int &ll,const int &rr) { 43 if( ll <= l && r <= rr ) return dat[pos]; 44 const int mid = ( l + r ) >> 1; 45 if( rr <= mid ) return query(lson(pos),l,mid,ll,rr); 46 else if( ll > mid ) return query(rson(pos),mid+1,r,ll,rr); 47 else return query(rson(pos),mid+1,r,ll,rr) * query(lson(pos),l,mid,ll,rr); 48 } 49 }sgt; 50 51 inline void addedge(int from,int to) { 52 static int cnt = 0; 53 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 54 } 55 inline void pre(int pos) { 56 siz[pos] = 1; 57 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) { 58 dep[t[at]] = dep[pos] + 1 , fa[t[at]] = pos , pre(t[at]) , siz[pos] += siz[t[at]]; 59 if( siz[t[at]] > siz[son[pos]] ) son[pos] = t[at]; 60 } 61 } 62 inline void dfs(int pos) { 63 ++iid , mxd[top[rec[id[pos]=iid]=pos]=pos==son[fa[pos]]?top[fa[pos]]:pos] = iid , h[pos] = f[pos] = inf; 64 if( son[pos] ) dfs(son[pos]) , f[pos] = f[son[pos]] , h[pos] = 0; // pos isn‘t a leaf node . 65 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] && t[at] != son[pos] ) dfs(t[at]) , h[pos] += f[t[at]]; 66 f[pos] = std::min( f[pos] + h[pos] , v[pos] ); 67 } 68 69 inline lli query(int pos) { 70 Matrix ret = sgt.query(1,1,n,id[pos],mxd[top[pos]]); 71 ret = ini * ret; 72 return ret[0][1]; 73 } 74 75 inline void update(int pos) { 76 while(pos) { 77 trans[pos][0][1] = v[pos] , trans[pos][1][1] = h[pos] , 78 sgt.update(1,1,n,id[pos]) , pos = top[pos]; 79 if( pos == 1 ) break; // root don‘t have fa . 80 Matrix fs = ini * sgt.query(1,1,n,id[pos],mxd[pos]); 81 h[fa[pos]] -= f[pos] , h[fa[pos]] += ( f[pos] = fs[0][1] ); 82 pos = fa[pos]; 83 } 84 } 85 86 inline char nxtchar() { 87 static const int BS = 1 << 21; 88 static char buf[BS],*st=buf+BS,*ed=st; 89 if( st == ed ) ed = buf + fread(st=buf,1,BS,stdin); 90 return st == ed ? -1 : *st++; 91 } 92 inline char realchar() { 93 char ret; 94 while( !isalpha(ret=nxtchar()) ); 95 return ret; 96 } 97 inline int getint() { 98 int ret = 0 , ch; 99 while( !isdigit(ch=nxtchar()) ); 100 do ret=ret*10+ch-‘0‘; while( isdigit(ch=nxtchar()) ); 101 return ret; 102 } 103 inline int getlli() { 104 lli ret = 0 , ch; 105 while( !isdigit(ch=nxtchar()) ); 106 do ret=ret*10+ch-‘0‘; while( isdigit(ch=nxtchar()) ); 107 return ret; 108 } 109 110 int main() { 111 static int m; 112 n = getint() , ini[0][0] = ini[0][1] = 0; 113 for(int i=1;i<=n;i++) v[i] = getlli(); 114 for(int i=1,a,b;i<n;i++) a = getint() , b = getint() , addedge(a,b) , addedge(b,a); 115 pre(1) , dfs(1); 116 for(int i=1;i<=n;i++) trans[i][0][0] = 0 , trans[i][0][1] = v[i] , trans[i][1][0] = inf , trans[i][1][1] = h[i]; 117 sgt.build(1,1,n); 118 m = getint(); 119 for(int i=1,o,p;i<=m;i++) { 120 o = realchar() , p = getint(); 121 if( o == ‘Q‘ ) printf("%lld\n",query(p)); 122 else if( o == ‘C‘ ) v[p] += getlli() , update(p); 123 } 124 return 0; 125 }
雪の降るこの街にも 暖かい光が差し
雪花飘飞的这条街道上 温暖光芒从天而降
折れた羽を癒してる 傷ついた心の奧
受伤心灵的深处 被祈愿之羽逐渐治愈
足音が聞こえてくる 明日への扉叩いて
我听到了谁的脚步声 有人在敲打通往明日的门扉
目の前の道を進む 季節が巡る 時の中で
季节更迭 我在时光之流中踏上眼前的道路
巡る想い あなただけ 笑顏が今もまぶしい
流连的思念 只有你的笑颜直到现在还如此炫目
标签:根据 end 转移 解法 isp alc closed 初始 char
原文地址:https://www.cnblogs.com/Cmd2001/p/9011712.html