标签:最小值 注意 除了 这一 需要 函数 cep 最小 解决
问题描述
假设有 1 元,3 元,5 元的硬币若干(无限),现在需要凑出 11 元,问如何组合才能使硬币的数量最少?
问题分析
乍看之下,我们简单的运用一下心算就能解出需要 2 个 5 元和 1 个 1 元的解。当然这里只是列出了这个问题比较简单的情况。当硬币的币制或者种类变化,并且需要凑出的总价值变大时,就很难靠简单的计算得出结论了。贪心算法可以在一定的程度上得出较优解,但不是每次都能得出最优解。
这里运用动态规划的思路解决该问题。按照一般思路,我们先从最基本的情况来一步一步地推导。
我们先假设一个函数 d(i) 来表示需要凑出 i 的总价值需要的最少硬币数量。
当 i = 0 时,很显然我们可以知道 d(0) = 0。因为不要凑钱了嘛,当然也不需要任何硬币了。注意这是很重要的一步,其后所有的结果都从这一步延伸开来。
当 i = 1 时,因为我们有 1 元的硬币,所以直接在第 1 步的基础上,加上 1 个 1 元硬币,得出 d(1) = 1。
当 i = 2 时,因为我们并没有 2 元的硬币,所以只能拿 1 元的硬币来凑。在第 2 步的基础上,加上 1 个 1 元硬币,得出 d(2) = 2。
当 i = 3 时,我们可以在第 3 步的基础上加上 1 个 1 元硬币,得到 3 这个结果。但其实我们有 3 元硬币,所以这一步的最优结果不是建立在第 3 步的结果上得来的,而是应该建立在第 1 步上,加上 1 个 3 元硬币,得到 d(3) = 1。
...
接着就不再举例了,我们来分析一下。可以看出,除了第 1 步这个看似基本的公理外,其他往后的结果都是建立在它之前得到的某一步的最优解上,加上 1 个硬币得到。得出:
d(i) = d(j) + 1
这里 j < i。通俗地讲,我们需要凑出 i 元,就在凑出 j 的结果上再加上某一个硬币就行了。
那这里我们加上的是哪个硬币呢。嗯,其实很简单,把每个硬币试一下就行了:
假设最后加上的是 1 元硬币,那 d(i) = d(j) + 1 = d(i - 1) + 1。
假设最后加上的是 3 元硬币,那 d(i) = d(j) + 1 = d(i - 3) + 1。
假设最后加上的是 5 元硬币,那 d(i) = d(j) + 1 = d(i - 5) + 1。
我们分别计算出 d(i - 1) + 1,d(i - 3) + 1,d(i - 5) + 1 的值,取其中的最小值,即为最优解,也就是 d(i)。
最后公式:
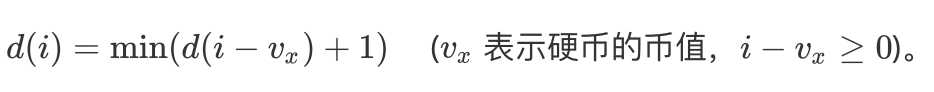
代码示例
public class CoinProblemBasicTest {
private int[] d; // 储存结果
private int[] coins = {1, 3, 5}; // 硬币种类
private void d_func(int i, int num) {
if (i == 0) {
d[i] = 0;
d_func(i + 1, num);
}
else {
int min = 9999999; // 初始化一个很大的数值。当最后如果得出的结果是这个数时,说明凑不出来。
for (int coin : coins) {
if (i >= coin && d[i - coin] + 1 < min) {
min = d[i - coin] + 1;
}
}
d[i] = min;
if (i < num) {
d_func(i + 1, num);
}
}
}
@Test
public void test() throws Exception {
int sum = 11; // 需要凑 11 元
d = new int[sum + 1]; // 初始化数组
d_func(0, sum); // 计算需要凑出 0 ~ sum 元需要的硬币数量
for (int i = 0; i <= sum; i++) {
System.out.println("凑齐 " + i + " 元需要 " + d[i] + " 个硬币");
}
}
}
结果如下:
凑齐 0 元需要 0 个硬币
凑齐 1 元需要 1 个硬币
凑齐 2 元需要 2 个硬币
凑齐 3 元需要 1 个硬币
凑齐 4 元需要 2 个硬币
凑齐 5 元需要 1 个硬币
凑齐 6 元需要 2 个硬币
凑齐 7 元需要 3 个硬币
凑齐 8 元需要 2 个硬币
凑齐 9 元需要 3 个硬币
凑齐 10 元需要 2 个硬币
凑齐 11 元需要 3 个硬币标签:最小值 注意 除了 这一 需要 函数 cep 最小 解决
原文地址:https://www.cnblogs.com/Roni-i/p/9011815.html