标签:exp ati nbsp 均值 hub body sse 改变 之间
整理自:
https://blog.csdn.net/woaidapaopao/article/details/77806273?locationnum=9&fps=1
1.Backpropagation(要能推倒)
后向传播是在求解损失函数L对参数w求导时候用到的方法,目的是通过链式法则对参数进行一层一层的求导。这里重点强调:要将参数进行随机初始化而不是全部置0,否则所有隐层的数值都会与输入相关,这称为对称失效。
大致过程是:
Step1:首先前向传导计算出所有节点的激活值和输出值
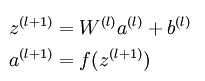
Step2:计算整体损失函数
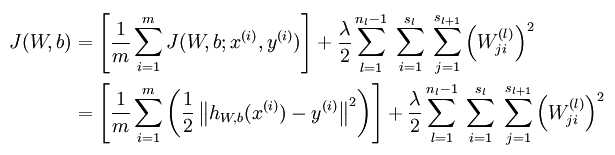
Step3:针对第L层的每个节点计算出残差(这里是因为UFLDL中说的是残差,本质就是整体损失函数对每一层激活值Z的导数),所以要对W求导只要再乘上激活函数对W的导数即可
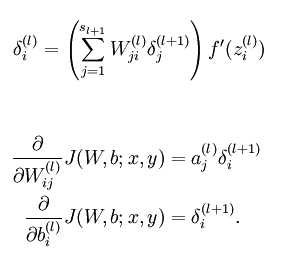
2.梯度消失、梯度爆炸
梯度消失:这本质上是由于激活函数的选择导致的, 最简单的sigmoid函数为例,在函数的两端梯度求导结果非常小(饱和区),导致后向传播过程中由于多次用到激活函数的导数值使得整体的乘积梯度结果变得越来越小,也就出现了梯度消失的现象。
梯度爆炸:同理,出现在激活函数处在激活区,而且权重W过大的情况下。但是梯度爆炸不如梯度消失出现的机会多。
3.常用的激活函数
| 激活函数 | 公式 | 缺点 | 优点 |
|---|---|---|---|
| Sigmoid | 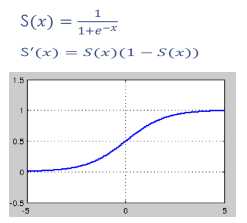 |
1、会有梯度弥散 2、不是关于原点对称 3、计算exp比较耗时 |
- |
| Tanh | 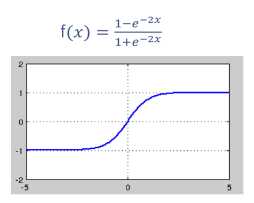 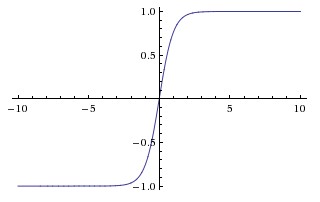 |
梯度弥散没解决; 还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失 |
1、解决了原点对称问题(输出以0为中心) 2、比sigmoid收敛速度更快 |
| ReLU | f(x)=max(0,x) |
梯度弥散没完全解决,在(-)部分相当于神经元死亡而且不会复活 | 1、解决了部分梯度弥散问题 2、收敛速度更快 |
| Leaky ReLU | 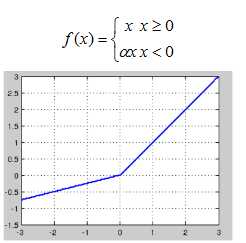
α建议为0.25 |
- | 解决了神经死亡问题 |
| Maxout | 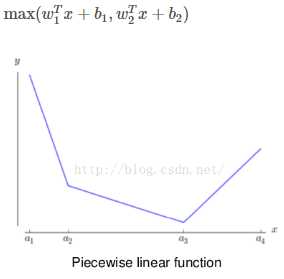
|
参数比较多,本质上是在输出结果上又增加了一层 | 克服了ReLU的缺点,比较提倡使用 |
4.参数更新方法
| 方法名称 | 公式 |
|---|---|
| Vanilla update | x += - learning_rate * dx |
| Momentum update动量更新 | v = mu * v - learning_rate * dx # integrate velocity x += v # integrate position |
| Nesterov Momentum | x_ahead = x + mu * v v = mu * v - learning_rate * dx_ahead x += v |
| Adagrad (自适应的方法,梯度大的方向学习率越来越小,由快到慢) |
cache += dx**2 x += - learning_rate * dx / (np.sqrt(cache) + eps) |
| Adam | m = beta1*m + (1-beta1)dx v = beta2*v + (1-beta2)(dx**2) x += - learning_rate * m / (np.sqrt(v) + eps) |
5.解决overfitting的方法
dropout, regularization, batch normalizatin,但是要注意dropout只在训练的时候用,让一部分神经元随机失活。
Batch normalization是为了让输出都是单位高斯激活,方法是在连接和激活函数之间加入BatchNorm层,计算每个特征的均值和方差进行规则化。
标签:exp ati nbsp 均值 hub body sse 改变 之间
原文地址:https://www.cnblogs.com/helloworld0604/p/9017030.html