标签:++ any lin gyp access 完整 ica span mini
POJ_1066_Treasure Hunt_判断线段相交
Description
Input
Output
Sample Input
7
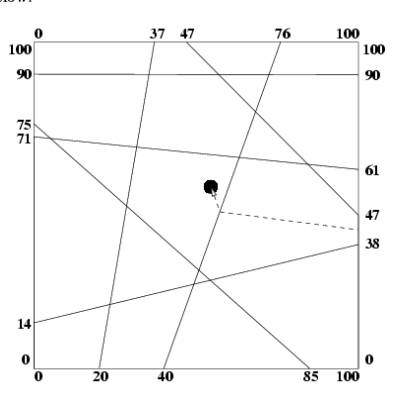
20 0 37 100
40 0 76 100
85 0 0 75
100 90 0 90
0 71 100 61
0 14 100 38
100 47 47 100
54.5 55.4
Sample Output
Number of doors = 2
来自古文物和古玩博物馆(ACM)的考古学家已经飞到埃及去研究大金字塔的大金字塔。
利用最先进的技术,他们能够确定金字塔的底层是由一系列的直线墙构成的,这些墙与许多封闭的房间相交。目前,没有任何门可以进入任何一个房间。
这种最先进的技术也精确定位了宝藏室的位置。
这些专门的(和贪婪的)考古学家想要做的是把门从墙上炸开,到达宝藏室。然而,为了尽量减少在中间的房间里对艺术作品的损害(并在政府的资助下,他们想要通过最少的门数来进行爆炸)。
出于结构完整性的目的,门应该只在进入房间的墙壁的中点被炸开。你要写一个程序来确定这个最小的门数。
注意是进入房间的墙壁的中点而不是直线墙的中点。
那样这道题就变得非常简单了,直接枚举每个点判断这个点与宝藏的连线经过多少条线段即可。
然后+1就是答案。
代码:
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#include <math.h>
using namespace std;
typedef double f2;
struct Point {
f2 x,y;
Point() {}
Point(f2 x_,f2 y_) :
x(x_),y(y_) {}
Point operator + (const Point &p) const {return Point(x+p.x,y+p.y);}
Point operator - (const Point &p) const {return Point(x-p.x,y-p.y);}
Point operator * (f2 rate) const {return Point(x*rate,y*rate);}
};
struct Line {
Point p,v;
Line() {}
Line(const Point &p_,const Point &v_) :
p(p_),v(v_) {}
};
f2 cross(const Point &p1,const Point &p2) {return p1.x*p2.y-p1.y*p2.x;}
f2 turn(const Point &p1,const Point &p2,const Point &p3) {
return cross(p3-p1,p2-p1);
}
bool judge(const Line &l1,const Line &l2) {
if(turn(l1.p,l1.v,l2.p)*turn(l1.p,l1.v,l2.v)>=0) return 0;
if(turn(l2.p,l2.v,l1.p)*turn(l2.p,l2.v,l1.v)>=0) return 0;
return 1;
}
Line a[50];
Point T;
int n;
int solve(const Line &l) {
int i,re=0;
for(i=1;i<=n;i++) {
if(judge(a[i],l)) re++;
}
return re;
}
int main() {
scanf("%d",&n);
if(!n) {
printf("Number of doors = %d",1); return 0;
}
int i;
int ans=1<<30;
for(i=1;i<=n;i++) {
scanf("%lf%lf%lf%lf",&a[i].p.x,&a[i].p.y,&a[i].v.x,&a[i].v.y);
}
scanf("%lf%lf",&T.x,&T.y);
for(i=1;i<=n;i++) {
Line l=Line(T,a[i].p);
ans=min(ans,solve(l));
l=Line(T,a[i].v);
ans=min(ans,solve(l));
}
printf("Number of doors = %d",ans+1);
}
标签:++ any lin gyp access 完整 ica span mini
原文地址:https://www.cnblogs.com/suika/p/9017777.html