组合数

标签：分解质因数   初始化   二层   ring   algorithm   初始   bsp   bre   out   

#include<cstdio>//分解质因数 二维前缀和

#include<iostream> #include<cmath>

#include<cstring> #include<iomanip>

#include<algorithm>

using namespace std;

int qz[2001][4];

int ans[2001][2001],answer[2001][2001];

int fk[4],kk[4];

int zhishu[9]={0,2,3,5,7,11,13,17,19};

int main()

{ int t,k; cin>>t>>k;

for(int i=1;i<=8;i++)

{ if(k%zhishu[i]==0) { fk[++fk[0]]=zhishu[i];

while(k%zhishu[i]==0) { k/=zhishu[i]; kk[fk[0]]++; } } }

for(int i=1;i<=2000;i++)

for(int j=1;j<=fk[0];j++)

{

qz[i][j]=qz[i-1][j];

int n=i;

while(n%fk[j]==0)

{ qz[i][j]++; n/=fk[j]; } }

for(int i=1;i<=2000;i++)

for(int q=1;q<=i;q++)

{ ans[q][i]=1;

for(int j=1;j<=fk[0];j++)

{ if(qz[i][j]-qz[q][j]-qz[i-q][j]<kk[j]) { ans[q][i]=0; break; } } }

for(int i=1;i<=2000;i++)

for(int j=1;j<=2000;j++)

{ answer[i][j]=answer[i-1][j]+answer[i][j-1]-answer[i-1][j-1];

if(ans[i][j]==1)answer[i][j]++; }

for(int i=1;i<=t;i++)

{ int m,n;

cin>>m>>n;

cout<<answer[n][m]<<endl; } }

var tra,ans:array[0..2000,0..2000]of longint;\tra[i,j]表示Cij(i为下标,j为上标)//dp

\ans[i,j]表示当n=i,m=j时的答案

    n,m:array[1..10000]of longint;
    i,j,t,k,mn:longint;
begin
  readln(t,k);
  for i:=1 to t do\\读入n,m
  begin
    readln(n[i],m[i]);
    if m[i]>n[i] then m[i]:=n[i];\\若m>n,则ans[n,m]=ans[n,n],所以令m=n
    if n[i]>mn then mn:=n[i];\\递推只需递推到最大的n即可
  end;
  for i:=0 to mn do\\初始化
    tra[i,0]:=1;
  tra[1,1]:=1;
  for i:=2 to mn do\\i直接从第二层递推
  begin
    for j:=1 to i do
    begin
      tra[i,j]:=tra[i-1,j]+tra[i-1,j-1];\\应用组合公式计算组合数
      if tra[i,j] mod k=0 then ans[i,j]:=1;\\若为k的倍数则答案加一
      tra[i,j]:=tra[i,j] mod k;
      ans[i,j]:=ans[i,j]+ans[i-1,j]+ans[i,j-1]-ans[i-1,j-1];\\答案的递推详情见下图
 ![](https://cdn.luogu.org/upload/pic/4157.png) 

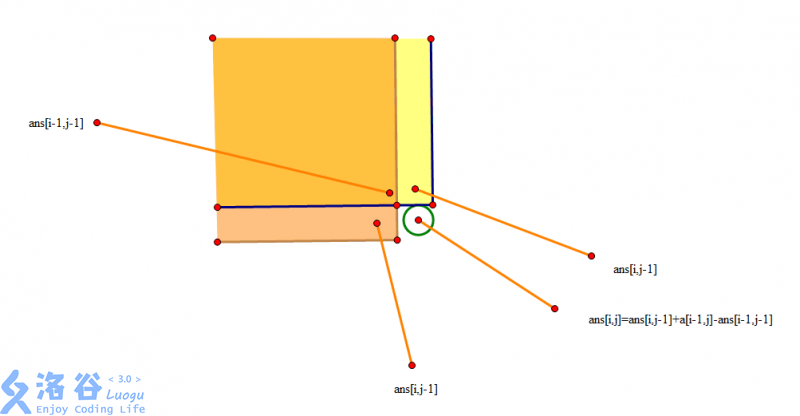\就是上面加上下面在减去重复的部分

    end;
    for j:=i+1 to mn do
      ans[i,j]:=ans[i,j]+ans[i-1,j]+ans[i,j-1]-ans[i-1,j-1];
  end;
  for i:=1 to t do
    writeln(ans[n[i],m[i]]);
end.

组合数

标签：分解质因数   初始化   二层   ring   algorithm   初始   bsp   bre   out   

原文地址：https://www.cnblogs.com/wyh447154317/p/9020098.html