标签:com code 数组 tps 元素 乘法 tle double subject
转载:https://www.cnblogs.com/zzqc/p/8995135.html
C.
链接:https://www.nowcoder.com/acm/contest/109/C
来源:牛客网
第一行两个整数n,k(1 <= n <= 2000, 0 <= k <= 1,000,000,000);i
第二行n个整数表示a数组(0 <= a
<= 1,000,000,000)。
一行n个整数表示答案。
3 1 1 2 3
1 3 6
5 0 3 14 15 92 6
3 14 15 92 6k
首先注意到这个操作可以用矩阵来表示,设原数组为一个行向量A,k次操作之后得到的行向量B, 转移矩阵为X,则有A*X
=B ,观察发现X是一个N*N的上三角矩阵,
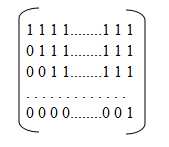
可即使使用了快速幂,这个矩阵一次乘法的时间复杂度也不允许接受,因为N<=2000,N^3过于庞大,枚举了这个矩阵的前几次方之后发现一个规律,这个矩阵只要知道
第一行的元素就可以推出这个全部的矩阵,每一列都来自于第一行的一个子段,再观察发现这些数字都是杨辉三角里的数,准确的说这一行数对应杨辉三角的一列(斜着),
对于X^k,这个矩阵,第一行的元素就是( C(k-1,0) , C(k,1) , C(k+1,2),.....C(k+n-2,n-1)),组合数的公式C(n,r)=C(n,r-1)*(n-r+1)/r,
C(n,r)=C(n-1,r)+C(n-1,r-1),联立得出C(n,r)=C(n-1,r-1)*n/r,有除法记得取逆元。
1 #include<iostream>
2 #include<cstring>
3 #include<queue>
4 #include<cstdio>
5 #include<stack>
6 #include<set>
7 #include<map>
8 #include<cmath>
9 #include<ctime>
10 #include<time.h>
11 #include<algorithm>
12 using namespace std;
13 #define mp make_pair
14 #define pb push_back
15 #define debug puts("debug")
16 #define LL long long
17 #define pii pair<int,int>
18 #define eps 1e-10
19 double R=6371009;
20
21 LL MOD=1e9+7;
22 LL q[2020];
23 LL a[2020];
24 void gcd(LL a,LL b,LL &d,LL &x,LL &y)
25 {
26 if(!b) {d=a;x=1;y=0;}
27 else {gcd(b,a%b,d,y,x);y-=x*(a/b);}
28 }
29 LL inv(LL a,LL n)
30 {
31 LL d,x,y;
32 gcd(a,n,d,x,y);
33 return d==1?(x+n)%n:-1;
34 }
35 int main()
36 {
37 LL n,m,i,j,k;
38 scanf("%lld%lld",&n,&k);
39 for(i=1;i<=n;++i) scanf("%lld",a+i);
40 k--;
41 q[1]=1;
42 for(i=2;i<=n;++i){
43 q[i]=q[i-1]*((k+i-1)%MOD)%MOD*inv(i-1,MOD);
44 q[i]%=MOD;
45 }
46 //for(i=2;i<=n;++i) q[i]+=q[i-1],q[i]%=MOD;
47 for(i=1;i<=n;++i){
48 LL tmp=0;
49 for(j=1;j<=i;++j){
50 tmp+=a[j]*q[i-j+1];
51 tmp%=MOD;
52 }
53 printf("%lld%c",tmp,i==n?‘\n‘:‘ ‘);
54 }
55 return 0;
56 }
标签:com code 数组 tps 元素 乘法 tle double subject
原文地址:https://www.cnblogs.com/vainglory/p/9021579.html