标签:gif 技术 include ima 方法 解法 更改 int span
赛题以及注意事项(下载):https://files.cnblogs.com/files/usingnamespace-caoliu/%E5%88%9D%E8%B5%9B.rar
第一题(已优化):
给定一个正数数组,找出不相邻元素的子序列的和的最大值。如:2、5、3、9应该返回14(5+9);8、5、3、9、1应该返回17(8+9);5 4 10 100 10 5应该返回110(5+100+5);

1 #include <stdio.h>
2 #include <unistd.h>
3
4 int max = 0;
5
6 void combination(int* arr,int i,int len)
7 {
8 if(i >= len)
9 {
10 int sum = 0;
11 for(int j=0; j<len-1; j++)
12 {
13 if(arr[j] && arr[j+1]) return;
14 sum += arr[j];
15 }
16
17 sum += arr[len-1];
18
19 if(sum > max)
20 {
21 max = sum;
22 }
23 return;
24 }
25
26 int tmep = arr[i];
27 arr[i] = 0;
28 combination(arr,i+1,len);
29 arr[i] = tmep;
30 combination(arr,i+1,len);
31 }
32
33 int main()
34 {
35 int t = 0;
36 scanf("%d",&t);
37 while(t--)
38 {
39 int n = 0;
40 scanf("%d",&n);
41 int arr[n];
42 for(int i=0; i<n; i++)
43 {
44 scanf("%d",&arr[i]);
45 }
46 combination(arr,0,n);
47 printf("%d\n",max);
48 }
49 }
思路:与大华模拟题第四题相同,利用递归函数遍历数组中任意位数相加的和,再通过if(arr[j] && arr[j+1]) return;剔除所有包含相邻元素的子序列的和,最后遍历所有符合题意的和,比较后即可得出不相邻元素的子序列的和的最大值。
总结:该方法为通用解法而非最优解,本质为递归嵌套,最终会形成一种类似于二叉树的结构,可通过更改递归最后一层的判定条件来实现绝大部分需遍历的功能。
第二题(已优化):
给定一个链表,实现一个函数,将链表中每k个节点进行翻转,若最后一组节点数量不足k个,则按实际个数翻转。例如:给定链表1->2->3->4->5->6->7->8->NULL,k=3,翻转后输出3->2->1->6->5->4->8->7->NULL。
翻转函数reverse有两个参数,分别为链表头指针和翻转步长k。

1 #include <stdio.h>
2
3 void _release(int* arr,int len)
4 {
5 for(int i=0; i<len/2; i++)
6 {
7 int t = arr[i];
8 arr[i] = arr[len-1-i];
9 arr[len-1-i] = t;
10 }
11 }
12
13 void release(int* arr,int k,int n)
14 {
15 if(k > n)
16 {
17 _release(arr,n);
18 return;
19 }
20 _release(arr,k);
21 release(arr+k,k,n-k);
22 }
23
24 int main()
25 {
26 int t = 0;
27 scanf("%d",&t);
28
29 while(t--)
30 {
31 int n = 0;
32 scanf("%d",&n);
33 int arr[n];
34 for(int i=0; i<n; i++)
35 {
36 scanf("%d",&arr[i]);
37 }
38
39 int k = 0;
40 scanf("%d",&k);
41 release(arr,k,n);
42
43 for(int i=0; i<n; i++)
44 {
45 printf("%d ",arr[i]);
46 }
47 printf("\n");
48 }
49 }
思路:该题可以通过数组来实现要求,按照题意将数组分割并分别翻转即可。同时要考虑到数组无法均分的情况。
总结:该题很简单,留意数组无法均分的情况即可。
第三题(已优化):
输入一个由大写字母‘A-Z’组成的字符串,按照如下方式,对字符串中的字符进行编码:
1.统计每个字符出现的次数,并根据出现次数对字符进行权重分配;
a.出现次数越高,权重越大; b.出现次数相同,字符值越小,权重越大; c.权重值为1~26,必须从1开始,连续分配,数值越大,权重越高;
2.把权重最小的两个字符构成二叉树的左右子节点,其和作为根节点(节点值为字符权重);
a.若两个子节点值不等,较小值作为左子节点;
b.若两个子节点值相同(多字符的权重和与另一个字符权重可能相同),则叶子节点作为左子节点;
3.重复过程2,直到根节点值为所有字符的权重和;
4.将树的左边定位0,右边定位1,从根节点到字符节点的路径,即为其编码值;
示例:
1.输入字符串‘MBCEMAMCBA’,各字符出现次数分别为M:3,A:2,B:2,C:2,E:1;
2.根据字符出现次数和字符大小,进行排序,结果为:M>A>B>C>E,对应权重值为 M:5,A:4,B:3,C:2,E:1
3.根据规则生成权重树:
a.(M:5,A:4,B:3,C:2,E:1)中E:1和C:2值最小,相加得3,则E:1为左节点,C:2为右节点,3为根节点;
b.(M:5,A:4,B:3,3)中B:3和3值最小,相加得6,则B:3为左节点,3为右节点,6为根节点;
c.(M:5,A:4,6)中M:5和A:4值最小,相加得9,则A:4为左节点,M:5为右节点,9为根节点;
d.(6,9)中只有两个值,相加得15,则6为左节点,9为右节点,15为根节点;
e.根节点达到所有字符的权重和1+2+3+4+5=15,结果如下:
15
0/ 1\
6 9
0/ 1\ 0/ 1\
B:3 3 A:4 M:5
0/ 1\
E:1 C:2

1 #include <stdio.h>
2 #include <stdlib.h>
3
4 typedef struct Node
5 {
6 char ch;
7 char code;
8 int count;
9 int weight;
10 struct Node* left;
11 struct Node* right;
12 }Node;
13
14 Node* create_node(void)
15 {
16 Node* node = malloc(sizeof(Node));
17 node->ch = 0;
18 node->weight = 0;
19 node->left = NULL;
20 node->right = NULL;
21 }
22
23 int ch_cnt = 0;
24 char arr_code[10000] = {};
25 Node arr_node[26] = {};
26
27 void count_weight(char* str)
28 {
29 for(int i=0,j=0; str[i]; i++)
30 {
31 for(j=0; j<ch_cnt; j++)
32 {
33 if(str[i] == arr_node[j].ch) break;
34 }
35
36 if(j<ch_cnt) continue;
37 arr_node[ch_cnt++].ch = str[i];
38 }
39
40 for(int i=0; i<ch_cnt; i++)
41 {
42 for(int j=0; str[j]; j++)
43 {
44 if(arr_node[i].ch == str[j]) arr_node[i].count++;
45 }
46 }
47
48 for(int i=0; i<ch_cnt-1; i++)
49 {
50 for(int j=i+1; j<ch_cnt; j++)
51 {
52 if(arr_node[i].count > arr_node[j].count ||
53 (arr_node[i].count==arr_node[j].count && arr_node[i].ch < arr_node[j].ch))
54 {
55 Node t = arr_node[i];
56 arr_node[i] = arr_node[j];
57 arr_node[j] = t;
58 }
59 }
60 }
61
62 for(int i=0; i<ch_cnt; i++)
63 {
64 arr_node[i].weight = i+1;
65 }
66 }
67
68 void create_tree(void)
69 {
70 if(ch_cnt<=1) return;
71
72 Node* root = create_node();
73 root->left = create_node();
74 root->right = create_node();
75
76 *(root->left) = arr_node[0];
77 *(root->right) = arr_node[1];
78
79 root->left->code = ‘0‘;
80 root->right->code = ‘1‘;
81
82 root->weight += root->left->weight;
83 root->weight += root->right->weight;
84
85
86 arr_node[1] = *root;
87
88 for(int i=0; i<ch_cnt-1; i++)
89 {
90 arr_node[i] = arr_node[i+1];
91 }
92
93 ch_cnt--;
94
95 for(int i=0; i<ch_cnt-1; i++)
96 {
97 for(int j=i+1; j<ch_cnt; j++)
98 {
99 if(arr_node[i].weight > arr_node[j].weight ||
100 (arr_node[i].weight == arr_node[j].weight&&!arr_node[i].ch))
101 {
102 Node t = arr_node[i];
103 arr_node[i] = arr_node[j];
104 arr_node[j] = t;
105 }
106 }
107 }
108 create_tree();
109 }
110 void show_tree(Node* tree)
111 {
112 if(NULL == tree) return;
113 show_tree(tree->left);
114 show_tree(tree->right);
115 }
116
117 int find_tree(Node* tree,char ch)
118 {
119 if(NULL == tree) return 0;
120 if(tree->ch == ch)
121 {
122 arr_code[ch_cnt++] = tree->code;
123 return 1;
124 }
125
126 if(find_tree(tree->left,ch) || find_tree(tree->right,ch))
127 {
128 arr_code[ch_cnt++] = tree->code;
129 }
130 }
131
132 int main()
133 {
134 int t = 0;
135 scanf("%d",&t);
136 char str[t][1000];
137 for(int i=0; i<t; i++)
138 {
139 gets(str[i]);
140 }
141 for(int i=0; i<t; i++)
142 {
143 count_weight(str[i]);
144 create_tree();
145 for(int j=0; str[i][j]; j++)
146 {
147 ch_cnt = 0;
148 find_tree(arr_node,str[i][j]);
149 for(int k=ch_cnt-1; k>=0; k--)
150 {
151 printf("%c",arr_code[k]);
152 }
153 }
154 }
155
156 }
方向:此题与哈夫曼树相关(哈夫曼树:https://blog.csdn.net/move_now/article/details/53398753)
思路一:以哈夫曼树为主体,在此基础上添加对字符串中各个字符分配权重的功能,最后分解字符串,根据各个字符的权重依次输出路径。
思路二:以每类字符为主体,创建储存各类字符信息的结构体,计算出各个字符的权重,延伸出两个空子叶,在此基础上根据各个字符的权重、按照题目规则将其连接成哈夫曼树形结构,最后分解字符串,根据各个字符的权重依次输出路径。
总结:总的来说,思路一是在现有哈夫曼树框架下进行代码的修改、添加,轮子已经造好,我们直接拿来用即可,能极大地减少实际代码量,但修改现有哈夫曼树代码时容易打乱自身思路且缺少创造性;思路二是以每类字符为主体,能在编写其结构体时有效的整理思路,整个程序关联性强,富有创造力,但程序难度较大。
PS :该程序本地测试无误,但上传后一直为0分,未能查明原因。
第四题:
实现find_sub_string(str1,str2)函数,判断字符串str2在str1中出现的次数。返回str2在str1中出现的次数。
int find_sub_string(const std::string& str1, const string& str2);
第五题:
有一个吃金币游戏:
1.地图中有N个城堡(编号分别为0~N-1),每个城堡中挂着一面旗子;
2.某些城堡之间是连通的,在其连通的路上,分散着若干个金币(个数可能相同,也可能不同);
3.玩家走过存在金币的路之后,可以获得这条路上的所有金币,同一条路走多次,只有第一次可获得金币;
游戏规则:
1.玩家可以从任意一个城堡出发;
2.玩家必须拿到所有城堡的旗子;
3.玩家走过的所有路,不能存在环路;
4.一定存在至少一条能让玩家拿到所有旗子的路线;
请设计一个算法,计算在遵守以上游戏规则的的前提下,最多能获取到的金币个数。
补充规则中对环路的说明:
1、环路就是最终走过的路径中存在圈,实例如下:
非环路: 环路:1-2-5-4-1则成为环路
1----2 3 1----2----3
| | | |
| | | |
4----5----6 4----5----6
| | | | |
| | | | |
7 8 9 7 8----9
2、如说明1中的路径,玩家走1-2-5-4-7-4-5,虽然无圈,但是4-7、5-4中的路径金币只能吃一次,重复走第二次金币不可以获取
第六题:
在H.264视频编码标准中,编码帧由NALU头和NALU主体组成,其中NALU头由一个字节组成。在实际编码时,在每个NAL前添加起始码 0x000001,解码器在码流中检测到起始码,当前NAL结束。
为了防止NAL内部出现0x000001的数据,在编码完一个NAL时,如果检测出有连续两个0x00字节,就在后面插入一个0x03。
当解码器在NAL内部检测到0x000003的数据,就把0x03抛弃,恢复原始数据。给定一组包含SPS NALU的编码数据,找出解码后的SPS数据。比如:
输入:{0x1f 0x00 0x00 0x01 0x67 0x42 0xd0 0x80 0x00 0x00 0x03 0x00 0x80 0x00 0x0f 0x00 0x00 0x01 0x68 0xce 0x3c 0x80},
处理:在上述例子中,第一个0x00 0x00 0x01为识别到的数据头,0x00 0x00 0x03 0x00数据中,0x03为需抛弃数据,第二个0x00 0x00 0x01为下一个数据头,那么取出两个数据头中间的数据并且抛弃掉此0x03,结果如下:{0x67 0x42 0xd0 0x80 0x00 0x00 0x00 0x80 0x00 0x0f }。
第七题:
给定一个全小写的英文字符串,请在该字符串中找到一个连续子字符串,使得子字符串没有重复的字符并且长度最长,计算此最长字符串的长度。比如:abcbdeab,最长的子字符串为cbdea,长度为5;aaaa,最长子字串为a,长度为1。
第八题:
一个数可以用二进制表示,也可以用十进制表示,如果该数的二进制表示法所有位数字之和等于十进制表示法所有位数字之和,则称该数为神奇数。比如:21(十进制)=10101(二进制),所有位数之和为2+1=3,1+0+1+0+1=3。求小于等于M的神奇数有多少个。
第九题:
我们来玩一个大富翁的游戏,在地图上有N个连续的城市,城市对某件商品的售价为[V1,V2,V3...VN],你作为未来的大富翁看到其中的商机,打起了倒卖商品赚取差价的主意。约束条件:你只能顺序从第一个城市出发,不能走回头路,每次只能交易一件商品,再下次买入商品后必须卖掉之前买入的商品,求你能赚取的最大财富。比如:城市商品售价为[1,9,2,3,8],最大财富为(9-1)+(8-2)=14;城市商品售价为[9,8,3,2,1],最大财富为0,因为你买啥都无法赚钱。
第十题:
假设你站在一棵二叉树的右边,从上往下,请输出你看到的节点。比如:
5 <---
/ \
2 3 <---
/ / \
4 6 8 <---
返回 538。
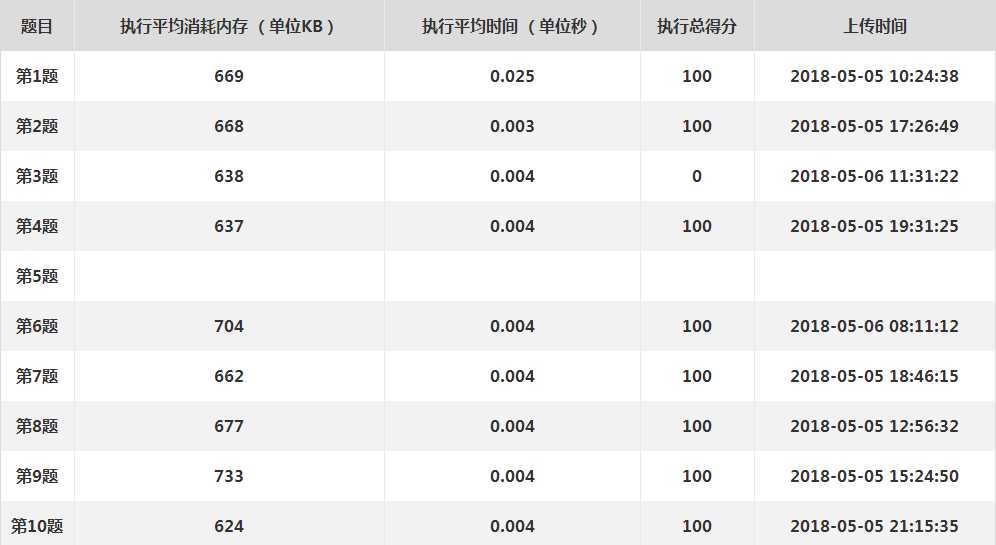
实现效果:
标签:gif 技术 include ima 方法 解法 更改 int span
原文地址:https://www.cnblogs.com/usingnamespace-caoliu/p/9027122.html