标签:添加 最大 理解 图片 line 函数 作者 org www
1、LR和SVM有什么相同点
(1)都是监督分类算法;
(2)如果不考虑核函数,LR和SVM都是线性分类算法,也就是说他们的分类决策面都是线性的;
(3)LR和SVM都是判别模型。
2、LR和SVM有什么不同点
(1)本质上是其loss function不同;
逻辑回归损失函数:
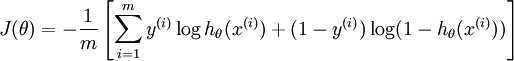
SVM损失函数:
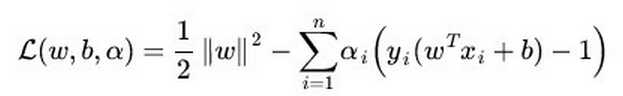
LR方法基于概率理论,假设样本为0或者1的概率可以用sigmoid函数来表示,然后通过极大似然估计的方法估计出参数的值,或者从信息论的角度来看,其是让模型产生的分布P(Y|X)P(Y|X)尽可能接近训练数据的分布;支持向量机?基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面 。
(2)SVM只考虑分类面上的点,而LR考虑所有点(远离的点对边界线的确定也起作用)
SVM中,在支持向量之外添加减少任何点都对结果没有影响,而LR则是每一个点都会影响决策。
Linear SVM不直接依赖于数据分布,分类平面不受一类点影响 ;LR则是受所有数据点的影响,所以受数据本身分布影响的,如果数据不同类别strongly unbalance,一般需要先对数据做balancing。?
(3)在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算量。 而LR则每个点都需要两两计算核函数,计算量太过庞大。
(4)SVM依赖于数据的测度,而LR则不受影响
因为SVM是基于距离的,而LR是基于概率的,所以LR是不受数据不同维度测度不同的影响,而SVM因为要最小化12||w||212||w||2所以其依赖于不同维度测度的不同,如果差别较大需要做normalization 。当然如果LR要加上正则化时,也是需要normalization一下的 。
使用梯度下降算法,一般都要 feature scaling,如果不归一化,各维特征的跨度差距很大,目标函数就会是“扁”的,在进行梯度下降的时候,梯度的方向就会偏离最小值的方向,走很多弯路。
(5)SVM自带结构风险最小化,LR则是经验风险最小化
SVM的损失函数就自带正则!!!(损失函数中的1/2||w||^2项),这就是为什么SVM是结构风险最小化算法的原因!!!而LR必须另外在损失函数上添加正则项!!!
以前一直不理解为什么SVM叫做结构风险最小化算法,所谓结构风险最小化,意思就是在训练误差和模型复杂度之间寻求平衡,防止过拟合,从而达到真实误差的最小化。未达到结构风险最小化的目的,最常用的方法就是添加正则项。
(6)LR和SVM在实际应用的区别
根据经验来看,对于小规模数据集,SVM的效果要好于LR,但是大数据中,SVM的计算复杂度受到限制,而LR因为训练简单,可以在线训练,所以经常会被大量采用【听今日头条的同学说,他们用LR用的就非常的多】
转自:简书作者
标签:添加 最大 理解 图片 line 函数 作者 org www
原文地址:https://www.cnblogs.com/eilearn/p/9026851.html