数学相关，先记账，再慢慢还……

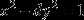
给定一个顶点均为整点（即坐标为整数的点）的简单多边形，其面积A和内部格点数目I与边上格点数目B的关系式：A=I+B/2-1.

三. 图论

3.1 柯尼希定理（最小顶点覆盖，二分图匹配，匈牙利算法）

图G的顶点覆盖是一个顶点集合V，使得G中的每一条边都接触V中的至少一个顶点。我们称集合V覆盖了G的边。最小顶点覆盖是用最少的顶点来覆盖所有的边。顶点覆盖数\tau是最小顶点覆盖的大小。
二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i ∈A,j ∈ B)，则称图G为一个二分图。
无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。
匈牙利算法：它是一种用增广路径求二分图最大匹配的算法。

四.组合数学

4.0  容斥原理

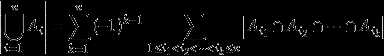
4.1 卡特兰数

是一串数列 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190

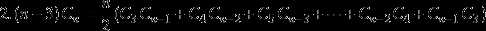
应用：

括号化
矩阵连乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种) [4]
出栈次序
一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列? [5-6]
输出序列的总数目=c(2n,n)-c(2n,n-1)=c(2n,n)/(n+1)=h(n)。
类似问题 买票找零
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少种方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)
凸多边形三角划分
在一个凸多边形中，通过若干条互不相交的对角线，把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n，求不同划分的方案数f（n）。比如当n=6时，f（6）=14。
即为f（n）=h（n-2） （n=2，3，4，……）。
类似问题
一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？
在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？
给定节点组成二叉搜索树
给定N个节点，能构成多少种不同的二叉搜索树？
（能构成h（N）个）
（这个公式的下标是从h(0)=1开始的）
n对括号正确匹配数目
给定n对括号，求括号正确配对的字符串数
假设S(n)为n对括号的正确配对数目，那么有递推关系S(n)=S(0)S(n-1)+S(1)S(n-2) +...+S(n-1)S(0)，显然S(n)是卡特兰数。

4.2.错排

D(n) = n! [(-1)^2/2! + … + (-1)^(n-1)/(n-1)! + (-1)^n/n!]. 

 4.3 鸽巢原理

原理1： 把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。
原理2 ：把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。
原理3 ：把无穷多件物体放入n个抽屉，则至少有一个抽屉里 有无穷个物体。

零.未分类定理

斯特林公式：当n足够大时，n!计算起来十分困难，虽然有很多关于n!的等式，但并不能很好地对阶乘结果进行估计，尤其是n很大之后，误差将会非常大。但利用Stirling公式可以将阶乘转化成幂函数，使得阶乘的结果得以更好的估计。

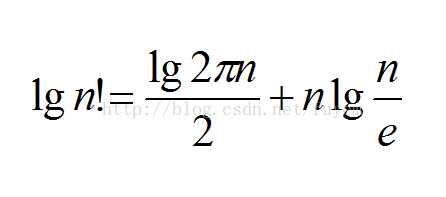
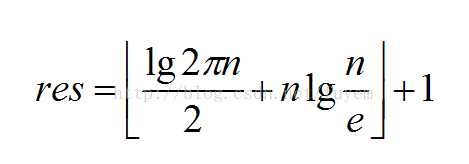
划分问题：

1、n个点最多把直线分成C(n,0)+C(n,1)份;

2、n条直线最多把平面分成C(n,0)+C(n,1)+C(n,2)份;

3、n个平面最多把空间分成C(n,0)+C(n,1)+C(n,2)+C(n,3)=(n3+5n+6)/6份;

4、n个空间最多把“时空”分成C(n,0)+C(n,1)+C(n,2)+C(n,3)+C(n,4)份.

卡特兰数：

Lucas定理

A、B是非负整数，p是质数。AB写成p进制：A=a[n]a[n-1]...a[0]，B=b[n]b[n-1]...b[0]。
则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0]) mod p同余
即：Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)
例子：poj 3146

五边形数定理

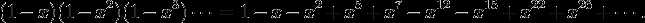
可用于生成函数(母函数)：
(1-x-x^2+x^5+x^7-x^12...)(1+p(1)x+p(2)x^2+p(3)x^3)=1;(整数划分的生成函数为1/∏(1-x^i))
得到p(n)=p(n-1)+p(n-2)-p(n-5)-p(n-7)+...

约瑟夫环

int result = 0;
for(int i = 2;i <= a;i++){
     result = (result+b) %i;
}