标签:ret 等于 记录 本质 子树查询 update tchar 来源 sub
主席树最基础可以维护区间K大的问题,由于其本质是可持久化线段树,所以要对线段树有很深的理解。
首先这种处理区间的问题肯定要想到区间数据结构。显然如果是指定了区间,可以把读入的数据离散化,然后建一颗值域线段树。
但是要在任意的[l,r]中查询第k小,一些大神就想到了前缀和。
首先建N颗线段树,第i棵维护区间a1-ai的每个数的出现个数。
此时值域线段树的结构都要保证完全相等,这样这些线段树就具有了可减性,就可以用前缀和维护了。
那这样就要建N棵线段树,空间无法承受。
我们可以轻易发现,维护a1-ai和a1-ai+1的线段树,的每一个非叶节点的子树有一半的结构都是相等的,如果能够只修改一半,空间的问题就会解决。
那如何处理空间了
比如说对于一个数1926,817,1989,604,首先离散化
于是 1926 就等价于3,以此类推。
那按照刚才的思路,我们可以先建一棵树维护a1-a1
如下图
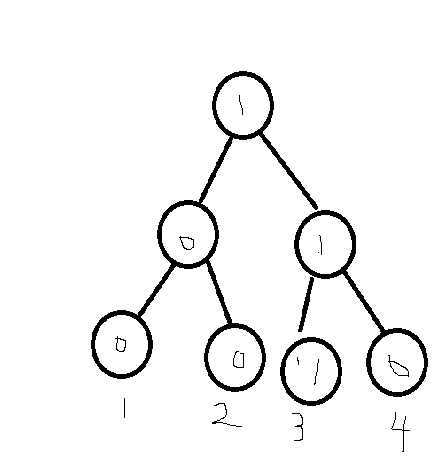
圆圈中的数字代表线段树维护的东西,也就是在这个区间内的数有多少个。
这个时候我们考虑建a1-a2的线段树,如果重新建这棵树会变成这样
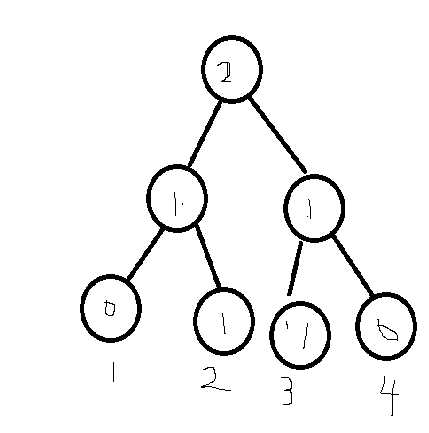
对比前一棵树,我们发现几乎一半的结构都是相同的。(圈出来的即为相同)
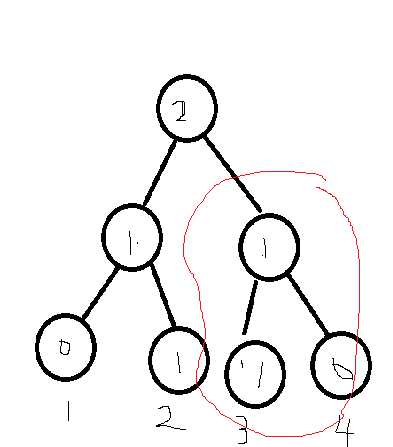
那我们每次先新建一个根节点:
其中维护a1-ai的根节点为rooti,如下图
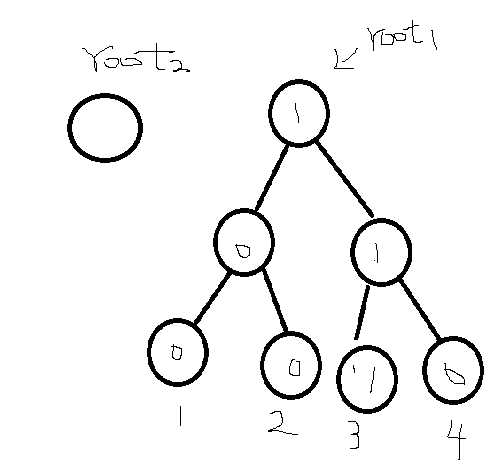
我们每一棵节点都要记录他左右儿子的编号(后面会解释)。
这样我们可以用让root2的右儿子的编号等于root1右儿子的编号相同的方式使root2的右儿子等于root1的左儿子且节约空间
个人感觉有点像链表:
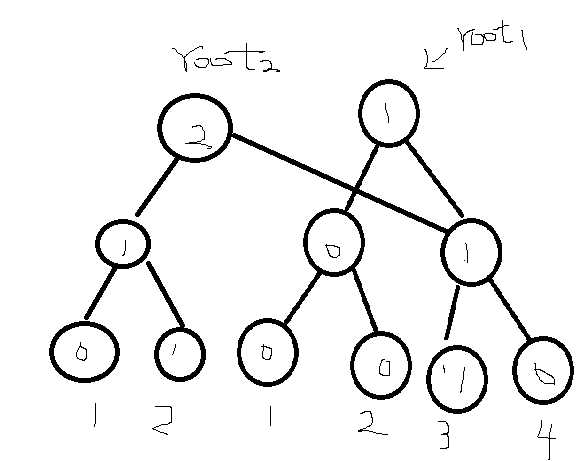
这样要修改的节点就大大减少了。
至于为什么要记录每个节点的左右儿子编号,正是因为主席树有一半的结构来源与前一棵树,这是这个节点与先前那个节点不构成线段树中i*2和i*2+1的关系
对于查询,我们要利用到前缀和:
对于查询,首先对于这棵子树查询K大:
我们只需要关注这棵子树的左子树出现的数的个数总和与K的大小关系:
如果小的话:在左子树查K小
如果大的话:往右子树查(k-左子树总和)小
那怎么知道L-R的个数:
前缀和,首先结构相同自然可以直接减啦!
至此静态主席树求静态第K小就搞定了,下面结合代码(非常丑陋):
#include<bits/stdc++.h> using namespace std; const int MAXN = 2 * 100000 + 10; inline int read() { int f = 1 ,x = 0; char ch; do { ch =getchar(); if(ch==‘-‘) f = -1; }while(ch<‘0‘||ch>‘9‘); do { x=(x<<3)+(x<<1)+ch-‘0‘; ch = getchar(); }while(ch>=‘0‘&&ch<=‘9‘); return f*x; } int n,m; struct node { int val; int id; friend bool operator < (node a1,node a2) { return a1.val<a2.val; } }; node a[MAXN]; int c[MAXN]; struct Tree { int lc; int rc; int sum; Tree() { sum = 0; } }; Tree tree[MAXN*20]; int root[MAXN]; int cnt =0; inline void init() { root[0]=0; tree[0].lc=tree[0].rc=0; tree[0].sum=0; return; } inline void update(int num,int &rt ,int l,int r) { tree[++cnt]=tree[rt]; rt = cnt; tree[rt].sum++; if(l==r) return; int mid = (l+r)>>1; if(num<=mid) update(num,tree[rt].lc,l,mid); else update(num,tree[rt].rc,mid+1,r); } inline int query(int l,int r,int k,int x,int y) { int now = tree[tree[r].lc].sum-tree[tree[l].lc].sum; if(x==y) return x; else { int mid = (x+y)>>1; if(now>=k) { return query(tree[l].lc,tree[r].lc,k,x,mid); } else return query(tree[l].rc,tree[r].rc,k-now,mid+1,y); } } int main() { n = read(); m = read(); for(int i=1;i<=n;i++) a[i].val=read(),a[i].id = i; sort(a+1,a+n+1); for(int i=1;i<=n;i++) { c[a[i].id]=i; } init(); for(int i=1;i<=n;i++) { root[i]=root[i-1]; update(c[i],root[i],1,n); } for(int i=1;i<=m;i++) { int L =read(); int R = read(); int k=read(); printf("%d\n",a[query(root[L-1],root[R],k,1,n)].val); } }
后面有空再填
标签:ret 等于 记录 本质 子树查询 update tchar 来源 sub
原文地址:https://www.cnblogs.com/wlzs1432/p/9019684.html